9. DRGANIA.

9.1. Oscylator liniowy ruchu drgającego prostego.

x = A E_c = E_p

x = 0 E_c = E_k

x = -A E_c = E_p

Siła harmoniczna ⇒ prawo Hook'a F= - kx

Siła wypadkowa F = ma ⇒ ma = -kx

II zasada dynamiki, równanie ruchu:

rozwiązanie równania:

gdzie

⇒
stąd

przyspieszenie:

Powtórzyć ruch punktu materialnego po okręgu!

Wyprowadzić związki pomiędzy :

• wychyleniem

• prędkością
  

• przyspieszeniem
  

ENERGIA: E_c = E_k + E_p

skoro
więc

czyli

Przykład:

dla

więc

Obwód LC

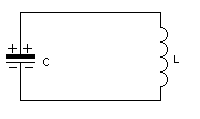
z zasady zachowania energii: E_c = E_sol + E_kond

różniczkując otrzymamy:

skoro
oraz

więc
⇒

analogie: drgania LC drgania mechaniczne

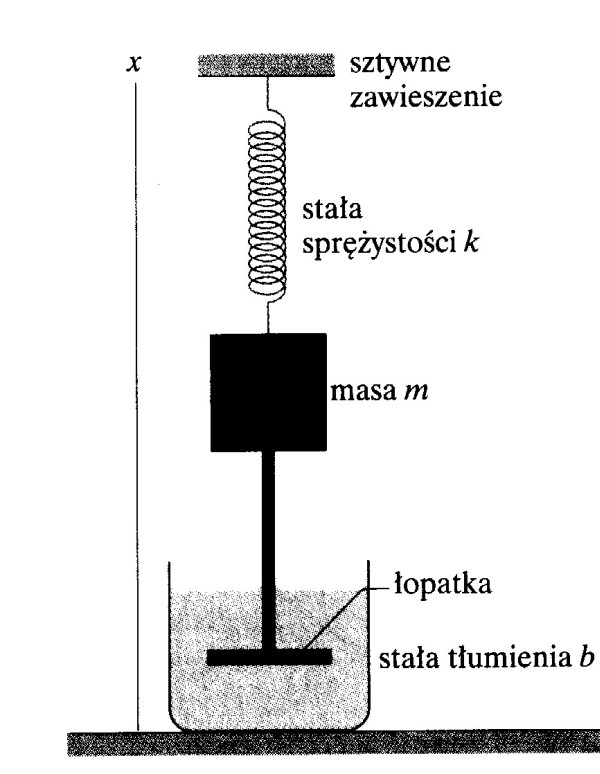
9.2. Drgania tłumione.

F_wypadkowa = F_{sprężystości} + F_oporu

ponieważ F_oporu = -bv (b - stała tłumienia)

więc ma = -kx - bv

gdzie
- współczynnik tłumienia

rozwiązanie:

po podstawieniu otrzymujemy:

jeśli β=0 (brak tłumienia)

to
ruch drgający prosty.

Obwód RLC szeregowy

Uc +UR +UL = 0

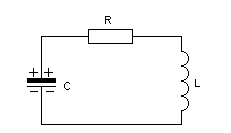
- II prawo Kirchoffa

podstawiając:
i

otrzymujemy:

Logarytmiczny dekrement tłumienia:

rozpatrując kolejne amplitudy

dekrement tłumienia jest miarą „oporu”

Słabe tłumienie:

• Drgania aperiodyczne - gasną po pierwszym wychyleniu .

• Wartość oporu krytycznego wyznacza warunek kiedy procesy periodyczne przechodzą w aperiodyczne.

---