Geometria przekrojów
Żebro |
|
Słup |
Hż = 50 cm |
|
B = 30 cm |
Bż = 30 cm |
|
H = 30 cm |
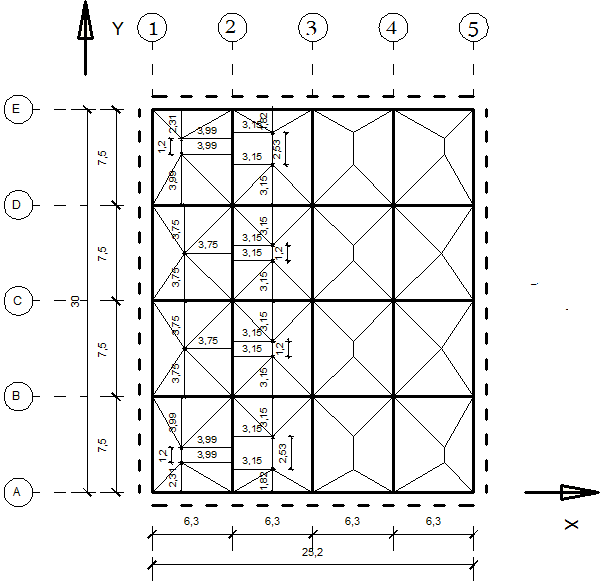
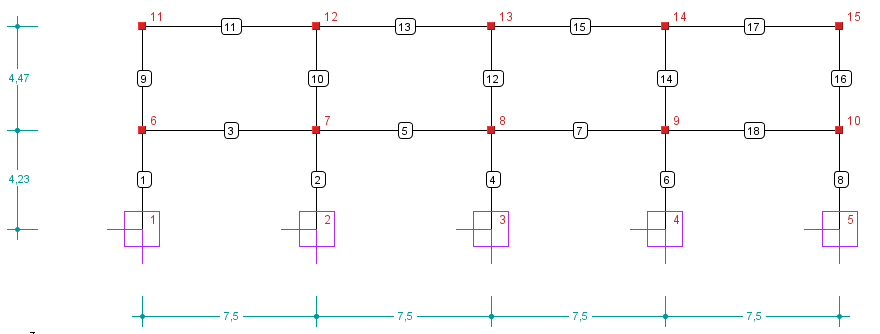
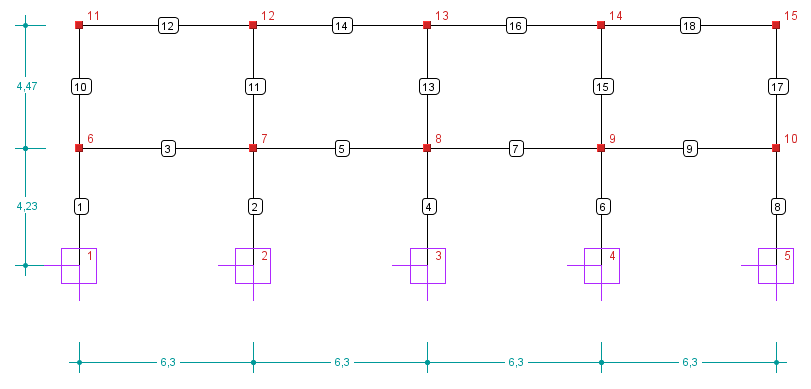
Schemat stropu
Obliczam słup w przecięciu ośi 2 oraz E.
Zebranie obciążeń
Obciążenia stałe g [kN/m]
Obciążenia zmienne p [kN/m]
Obciążenie zmienne śniegiem
Obciążenia stałe Δg [kN/m]
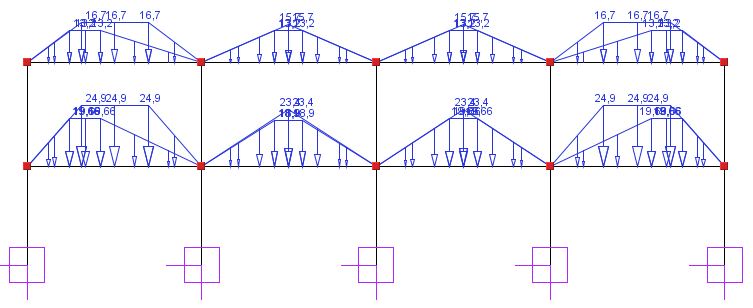
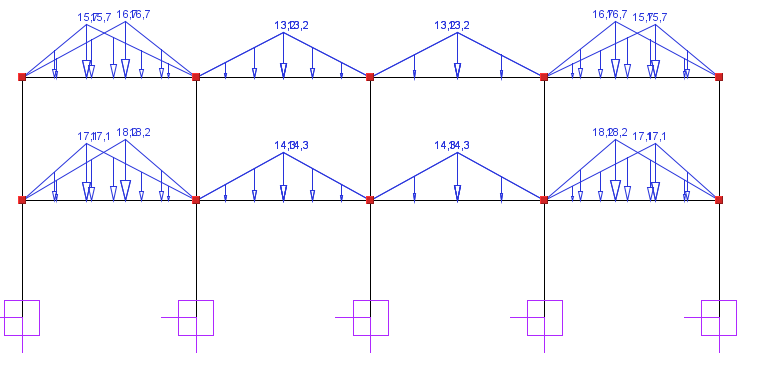
Schemat statyczny żebra, schemat obciążenia i wyniki dla osi liczbowej
Schemat statyczny
Schematy obciążeń
Schemat 1
Schemat 2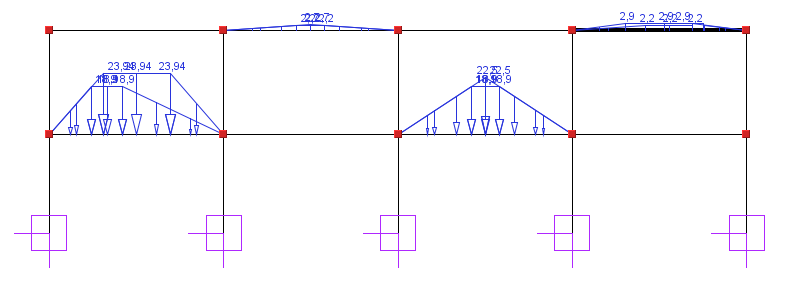
Schemat 3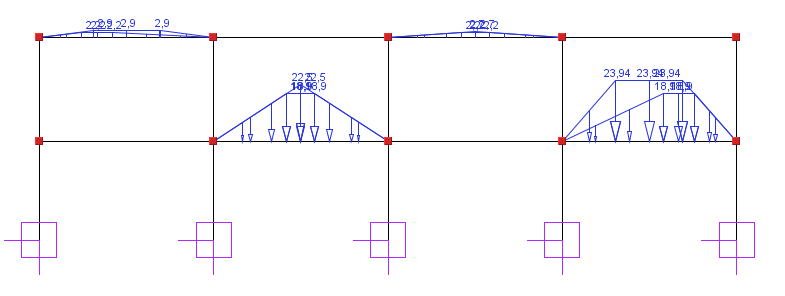
Schemat statyczny żebra, schemat obciążenia i wyniki dla osi literowychSchemat statyczny
Schematy obciążeń
Schemat 1
Obciążenie stałe g
Obciążenie stałe Δg
Schemat 2
Schemat 3
Wyniki
Wymiarowanie zbrojenia
Dane materiałowe:
Otulenie prętów zbrojenia
Wyznaczenie smukłości słupa
Wyznaczenie mimośrodu
Dla zbrojenia względem osi liczbowych
Dla kombinacji 1
Głowica słupa
Rodzaj obciążenia |
gk |
Żebro 0,5 m * 0,3 m * 25 kN/m3 |
3,75 |
Tynk cem - wap 0,015 m * (0,5 + 0,3 * 2 ) m * 21 kN/m3 |
0,35 |
SUMA |
4,1 |
Obliczam największe rzędne dla każdego trapezu obciążeń poszczególnych belek od obciążenia zmiennego.
Obciążenie użytkowe jest równe 6,0 kN/m2.
Miejscowość Koszalin znajduję się w strefie 2 obciążenia śniegiem według PN-EN 1991-1-3
wartość charakterystyczna obciążenia śniegiem gruntu: sk = 0,9 kN/m 2
współczynnik ekspozycji Ce = 1,0; współczynnik termiczny Ct = 1,0
Współczynnik kształtu dachu wynosi μ1 = 0,8.
Wartość charakterystyczna obciążenia śniegiem dachu: s = μ1 Ce Ct sk = 0,8 * 1,0 * 1,0 * 0,9 = 0,72 kN/m 2
Zebranie obciążeń dla płyty.
Rodzaj obciążenia |
gk |
Parkiet 0,015 m * 0,09 kN/m3 |
0,0014 |
Jastrych 0,03 m * 16 kN/m3 |
0,48 |
Styropian EPS 0,017 m * 0,45 kN/m3 |
0,008 |
Strop żelbetowy 0,15 m * 25 kN/m3 |
3,75 |
Styropian 0,06 m * 0,45 kN/m3 |
0,027 |
Tynk cem-wap 0,015 m * 19 kN/m3 |
0,285 |
SUMA [kN/m2] |
4,55 |
Zebranie obciążeń dla stropu
Rodzaj obciążenia |
gk |
Keramzyt 0,05 m * 2,9 kN/m3 |
0,145 |
Styropian EPS 0,017 m * 0,45 kN/m3 |
0,008 |
Strop żelbetowy 0,15 m * 25 kN/m3 |
3,75 |
Tynk cem-wap 0,015 m * 19 kN/m3 |
0,285 |
SUMA [kN/m2] |
4,188 |
Obliczam największe rzędne dla każdego trapezu obciążeń poszczególnych belek od obciążenia stałego, zmiennego.
Dla osi liczbowych.
Rodzaj obciążenia |
gk (4,1 kN/m2) [kN/m] |
Pk (6,0 kN/m2) [kN/m] |
sk( 0,72 kN/m2) [kN/m] |
Δgk (4,55 kN/m2) [kN/m] |
Δgk (4,188 kN/m2) [kN/m] |
A - B i D - E 3,99 m |
24,9 |
23,9 |
2,9 |
18,2 |
16,7 |
A - B i D - E 3,15 m |
19,66 |
18,9 |
2,2 |
14,3 |
13,2 |
B - C i C - D 3,75 m |
23,4 |
22,5 |
2,7 |
17,1 |
15,7 |
B - C i C - D 3,15 m |
19,66 |
18,9 |
2,2 |
14,3 |
13,2 |
Dla osi literowych.
Rodzaj obciążenia |
gk (4,1 kN/m2) [kN/m] |
Pk (6,0 kN/m2) [kN/m] |
sk( 0,72 kN/m2) [kN/m] |
Δgk (4,55 kN/m2) [kN/m] |
Δgk (4,188 kN/m2) [kN/m] |
1- 2 i 4 - 5 3,99 m |
24,9 |
23,9 |
2,9 |
18,2 |
16,7 |
1 - 2 i 4 - 5 3,75 m |
23,4 |
22,5 |
2,7 |
17,1 |
15,7 |
2 - 3 i 3 - 4 3,15 m |
19,66 |
18,9 |
2,2 |
14,3 |
13,2 |
Obciążenie stałe g
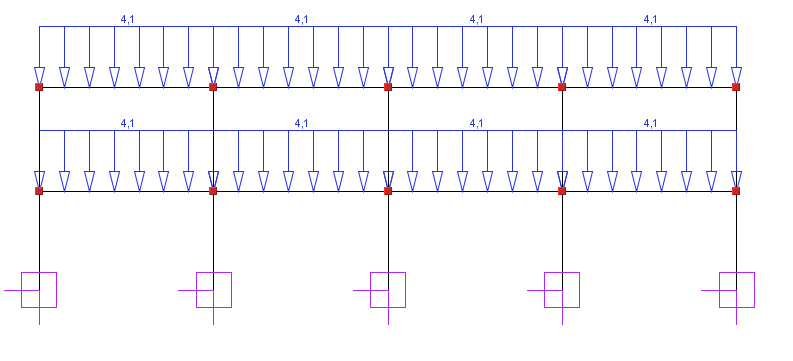
Obciążenie stałe Δg
Obciążenie zmienne p i śniegiem
Obciążenie zmienne p i śniegiem
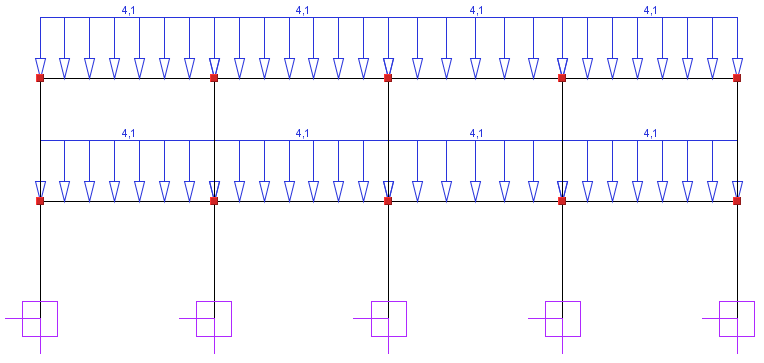
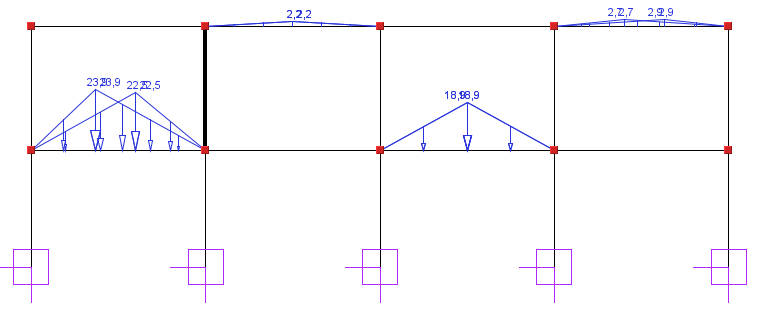
Obciążenie zmienne p i śniegiem
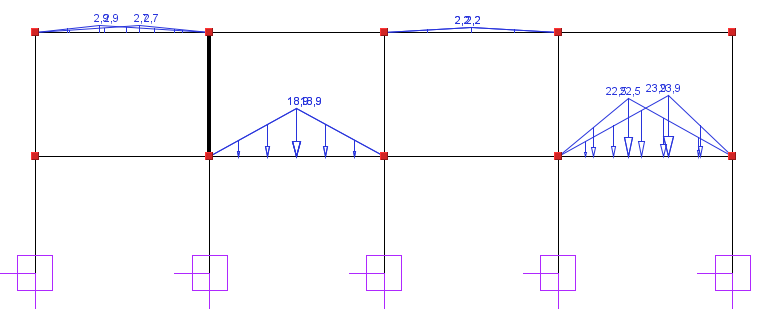
Obciążenie zmienne p i śniegiem
M1 - moment w przekroju głowicy słupa
M2 - moment u podstawy słupa
Wyniki dla osi liczbowej (Y-Y) |
|||
|
Komb 1 |
Komb 2 |
Komb 3 |
M1 [kNm] |
28,40 |
72,49 |
-30,53 |
M2 [kNm] |
-14,16 |
-39,36 |
18,46 |
T [kNm] |
-10,06 |
-26,44 |
11,58 |
N1 [kNm] |
-885,25 |
-745,26 |
-730,92 |
N2 [kNm] |
-921,22 |
-762,73 |
-748,40 |
Wyniki dla osi literowej (Z-Z) |
|||
|
Komb 1 |
Komb 2 |
Komb 3 |
M1 [kNm] |
42,24 |
43,72 |
20,32 |
M2 [kNm] |
-21,61 |
-22,00 |
-10,73 |
T [kN] |
-15,09 |
-15,53 |
-7,34 |
N1 [kN] |
-672,55 |
-537,53 |
-497,66 |
N2 [kNm] |
-690,02 |
-555,01 |
-515,14 |
|
|
|
|
Suma N1 [kN] |
-1557,80 |
-1282,79 |
-1228,58 |
Suma N2 [kN] |
-1611,24 |
-1317,74 |
-1263,54 |
Beton C30/37
fck = 30 MPa - wytrzymałość charakterystyczna na ściskanie
αcc = 0,8
fcd = fck/γc = 30/1,5*0,8 = 16,0 MPa - wytrzymałość obliczeniowa na ściskanie
fctm = 2,9 MPa - wytrzymałość średnia na rozciąganie
Ecm = 30 GPa - moduł sprężystości betonu
(norma PN-EN-1992-1-1, tablica 3.1)
Stal A-IIIN
fyk = 500 MPa - charakterystyczna granica plastyczności stali
fyd = fyk/γs = 410/1,15 = 434,78 MPa - obliczeniowa granica plastyczności stali
Es = 200 GPa - moduł sprężystości stali
ξeff,lim = 0,50 [-] - względna graniczna wysokość strefy ściskanej
cnom = cmin + ∆cdev
cmin = max (cmin,b; cmin,dur + ∆cdur,γ - ∆cdur,st - ∆cdur,add; 10 mm)
cmin = max (φ = 16 mm; 25 mm + 0 - 0 - 0; 10 mm) = 25 mm - dla klasy ekspozycji XC4, klasy konstrukcji S3 oraz stali zwykłej φ = 16 mm
∆cdev = 5 mm (należy zapewnić kontrolę otuliny podczas wykonywania)
cnom = 25+ 5 = 30 mm
Długość wyboczeniowa
lo = loy = loz = 4,23 * 0,7 = 2,96 m
Λlim = 20 *A * B * C / (n)^(0,5)
A = 0,7 (przyjęto)
B = 1,1 (przyjęto)
C = 0,7 (przyjęto)
n = Ned / ( b * h * fcd ) = 1489,03/ ( 30 * 30 * 16,0 / 10 ) = 0,340
Λlim = 20 *A * B * C / (n)^(0,5) = 20 *0,7 * 1,1 * 0,7 / (0,340)^(0,5) = 18,488
Λ = Λy = Λz = lo / b * (12) ^ ( 0,5) = 2,96 / 0,3 * (12) ^ ( 0,5) = 34,179
Λ = 34,179 > Λlim = 18,488 Należy uwzględnić efekty II rzędu
Mimośród niezamierzony dla każdej kombinacji i kierunku jest taki sam.
Ea = max( lo / 400; b / 30; 0,02 m) = max( 2,96 / 400; 0,3 / 30; 0,02 m) = max( 0,01; 0,01; 0,02 m) = 0,02 m
mimośród statyczny ee = Med / Ned = 28,39 / 885,25 = 0,03 m
mimośród początkowy e0 = ee + ea = 0,02 + 0,03 = 0,05 m
Resztę przypadków przedstawiono w tabeli
|
|
Głowica |
|
|
|
Podstawa |
|
|
|
|
|
Y-y |
|
Z-z |
` |
Y-y |
|
Z-z |
|
|
|
komb1 |
komb2 |
komb1 |
komb2 |
komb1 |
komb2 |
komb1 |
komb2 |
ea |
m |
0,02 |
0,02 |
0,02 |
0,02 |
0,02 |
0,02 |
0,02 |
0,02 |
Med |
kNm |
28,40 |
72,49 |
42,24 |
43,72 |
14,16 |
39,36 |
21,61 |
22,00 |
N |
kN |
1557,80 |
1282,79 |
1557,80 |
1282,79 |
1600,00 |
1200,00 |
1600,00 |
1200,00 |
ee |
m |
0,02 |
0,06 |
0,03 |
0,03 |
0,01 |
0,03 |
0,01 |
0,02 |
e0 |
m |
0,04 |
0,08 |
0,05 |
0,05 |
0,03 |
0,05 |
0,03 |
0,04 |
Wyznaczanie zbrojenia z uwagi na zginanie
Minimalny przekrój zbrojenia podłużnego
Asmin = maks ( 0,1 * Ned / fyd; 0,002 * Ac)
Zbrojenie minimalne obliczono dla największej wartości siły podłużnej
Asmin = mask ( 0,1 * 1489,03/ 35,6522; 0,002 * 30 * 30 ) = maks( 4,18; 1,80) = 4,8 cm2
Maksymalny przekrój zbrojenia podłużnego
Asmaks= 0,04 * Ac = 0,04 * 35 ^ 2 = 49 cm2
Zbrojenie podłużne
Dane:
h = b = 35 cm
a1 = a2 = 4,8 cm
d = h - a1 = 30,2 cm
Zbrojenie podłużne w przekroju głowicy w kierunku Y-Y dla kombinacji 1
Nsd = 1557,80 kN
przyjęto η = 1,1
e0 = 3,82 cm
etot = e0 * η = 3,82 * 1,030 = 4,21 cm
As1,min = As2,min = maks( 0,1 * Ned / fyd; 0,002 * Ac) = maks( 0,1 * 1557,8 / 434,78 / 10; 0,002 * 35 * 35) = 1,7914 cm2
es1= etot+ 0.5h − a1= 3,82 + 0,5 * 35 - 4,8 = 16,91 cm
es2= etot− 0.5h + a2 = 3,82 - 0,5 * 35 - 4,8 = -8,49 cm
ξeff=Nsd/(b*d*fcd) = 1557,8 / ( 35 * 302 * 11,33 / 10 ) = 1,3
Przyjmuję duży mimośród ξeff,lim = ξeff
As2 = (Nsd*es1-ξeff*(1-0,5*ξeff)*fcd*b*d^2)/(fyd*(d-a2))= (1557,80*16,64-0,53*(1-0,5*0,53)*20,0/10*35*30,2 ^2)/(434,78/10*(30,2 -4,8 ))= 6,91cm2
Jeżeli As2 >= As2,min
As1=(ξeff*b*d*fcd+As2*fyd-Ned)/fyd=(0,53*35*30,2*20+6,91*434,78-1557,8)/434,78 =-8,3cm2
Jeżeli w którymś z wcześniejszych przypadków As1<0 i As2>0 to mamy mały mimośród.
es2=0,5*h-etot-a2 = 0,5 * 35 - 4,21 - 4,8 = 7,73 cm
xeff=a2+(a2^2+2*Nsd*es2/(b*fcd))^(0,5) = 4,8+ (4,8 ^ 2 + 2 * 1557,80 * 7,73 / ( 35 * 20 / 10 ) ^ (0,5) = 26,09 cm
Jeżeli xeff,lim < xeff <= d
As2=(Nsd-xeff*b*fcd)/fyd = ( 1557,80 * 26,09 * 35 * 20 ) / 434,78 = 2,23 cm2
przyjęto As1 = As2 = 6,28 cm2 dla 2ϕ20
Resztę przypadków przedstawiono w tabeli
|
|
|
|
Głowica |
Podstawa |
||||||
|
|
|
|
Y-y |
Z-z ` |
Y-y |
Z-z |
||||
|
|
|
|
komb1 |
komb2 |
komb1 |
komb2 |
komb1 |
komb2 |
komb1 |
komb2 |
Dane |
kN |
Nsd |
= |
1557,80 |
1282,79 |
1557,80 |
1282,79 |
1611,24 |
1317,74 |
1611,24 |
1317,74 |
Moduł Younga |
Gpa |
Ecm |
= |
30,00 |
30,00 |
30,00 |
30,00 |
30,00 |
30,00 |
30,00 |
30,00 |
Moduł Younga |
Gpa |
Es |
= |
200,00 |
200,00 |
200,00 |
200,00 |
200,00 |
200,00 |
200,00 |
200,00 |
|
|
fck |
= |
20,00 |
20,00 |
20,00 |
20,00 |
20,00 |
20,00 |
20,00 |
20,00 |
Materiał |
MPa |
fcd |
= |
16,00 |
16,00 |
16,00 |
16,00 |
16,00 |
16,00 |
16,00 |
16,00 |
|
MPa |
fyd |
= |
434,780 |
434,780 |
434,780 |
434,780 |
434,780 |
434,780 |
434,780 |
434,780 |
|
- |
ξeff,lim |
= |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
Geometria |
cm |
b |
= |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
|
cm |
h |
= |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
|
cm |
a1 |
= |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
|
cm |
a2 |
= |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
|
cm |
d |
= |
30,20 |
30,20 |
30,20 |
30,20 |
30,20 |
30,20 |
30,20 |
30,20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
η |
= |
1,300 |
1,220 |
1,300 |
1,300 |
1,300 |
1,300 |
1,300 |
1,300 |
e0=ee+ea |
cm |
e0 |
= |
3,82 |
7,65 |
4,71 |
5,41 |
2,88 |
4,99 |
3,34 |
3,67 |
'ηe(s + ea) |
cm |
etot |
= |
4,97 |
9,33 |
6,12 |
7,03 |
3,74 |
6,48 |
4,34 |
4,77 |
|
|
|
|
|
|
|
|
|
|
|
|
Obliczenia |
|
|
|
|
|
|
|
|
|
|
|
|
cm2 |
As1,min=As2,min |
= |
1,7915 |
1,4752 |
1,7915 |
1,4752 |
1,8529 |
1,5154 |
1,8529 |
1,5154 |
es1= etot+ 0.5h − a1 |
cm |
es1 |
= |
17,67 |
22,03 |
18,82 |
19,73 |
16,44 |
19,18 |
17,04 |
17,47 |
es2= etot− 0.5h + a2 |
cm |
es2 |
= |
-7,73 |
-3,37 |
-6,58 |
-5,67 |
-8,96 |
-6,22 |
-8,36 |
-7,93 |
ξeff=Nsd/(b*d*fcd) |
- |
ξeff |
= |
0,92 |
0,76 |
0,92 |
0,76 |
0,95 |
0,78 |
0,95 |
0,78 |
|
- |
2*a2/d |
= |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
|
|
|
|
|
|
|
|
|
|
|
|
Przyjmuję duży mimośród ξeff,lim = ξeff |
|||||||||||
As2 = (Nsd*es1-ξeff*(1-0,5*ξeff)*fcd*b*d^2)/(fyd*(d-a2)) |
cm2 |
As2 |
= |
6,9094 |
7,58 |
8,54 |
4,90 |
5,97 |
4,87 |
6,85 |
2,83 |
Przyjmujemy As2 takie jakie mamy w słupie |
|
|
|
|
|
|
|
|
|
|
|
Jeżeli As2 >= As2,min |
|
|
|
|
|
|
|
|
|
|
|
As1=(ξeff*b*d*fcd+As2,prov*fyd-Ned)/fyd |
cm2 |
As1 |
= |
-8,30 |
-1,31 |
-6,68 |
-3,99 |
-10,47 |
-4,82 |
-9,59 |
-6,86 |
Jeżeli As2 < As2,min |
|
|
|
|
|
|
|
|
|
|
|
Przyjmuję As2,prov = As2,min |
cm2 |
As2,prov |
= |
- |
- |
- |
- |
- |
- |
- |
- |
Przyjmujemy As2 takie jakie mamy w słupie |
|
|
|
|
|
|
|
|
|
|
|
µeff=(Nsd*es1-As2,prov*fyd*(d-s2))/(b*d^2*fcd) |
- |
µeff |
= |
- |
- |
- |
- |
- |
- |
- |
- |
ξeff=1-(1-2*µeff)^(0,5) |
- |
ξeff |
= |
- |
- |
- |
- |
- |
- |
- |
- |
xeff=ξef*d |
cm |
xeff |
= |
- |
- |
- |
- |
- |
- |
- |
- |
Jeżeli xeff >= 2*a2 |
|
|
|
|
|
|
|
|
|
|
|
As1=(ξeff*b*d*fcd-Ned)/fyd + As2,prov |
cm2 |
As1 |
= |
- |
- |
- |
- |
- |
- |
- |
- |
Jeżeli xeff < 2*a2 |
|
|
|
|
|
|
|
|
|
|
|
As1=-Nsd*es2/(fyd*(d-a2)) |
cm2 |
As1 |
= |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jeżeli A s1 < 0 i A s2 ≤ 0 mamy przyjęte zbyt duże wymiary przekroju |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jeżeli w którymś z wcześniejszych przypadków As1<0 i As2>0 to mamy mały mimośród. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
es2=0,5*h-etot-a2 |
cm |
es2 |
= |
7,73 |
3,37 |
6,58 |
5,67 |
8,96 |
6,22 |
8,36 |
7,93 |
xeff=a2+(a2^2+2*Nsd*es2/(b*fcd))^(0,5) |
cm |
xeff |
= |
26,09 |
18,11 |
24,52 |
21,62 |
28,01 |
22,57 |
27,25 |
24,71 |
|
|
|
|
|
|
|
|
|
|
|
|
Jeżeli xeff,lim < xeff <= d |
|
|
|
|
|
|
|
|
|
|
|
As2=(Nsd-xeff*b*fcd)/fyd |
cm2 |
As2 |
= |
2,23 |
6,17 |
4,25 |
1,66 |
0,99 |
1,24 |
1,96 |
-1,51 |
As2=As2,min |
|
As2 |
= |
1,79 |
1,48 |
1,79 |
1,48 |
1,85 |
1,52 |
1,85 |
1,52 |
As1=As1,min |
|
As1 |
= |
1,79 |
1,48 |
1,79 |
1,48 |
1,85 |
1,52 |
1,85 |
1,52 |
|
|
|
|
|
|
|
|
|
|
|
|
Jeżeli xeff > d |
|
|
|
|
|
|
|
|
|
|
|
As2=(Nsd*es1-0,5*b*d^2*fcd)/(fyd*(d-a2)) |
cm2 |
As2 |
= |
- |
- |
- |
- |
- |
- |
- |
- |
As2=As2,min |
|
As2 |
= |
- |
- |
- |
- |
- |
- |
- |
- |
As1=(Nsd-b*d*fcd)/fyd-As2,prov |
cm2 |
As1 |
= |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
cm2 |
As2,prov |
= |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
|
cm2 |
As1,prov |
= |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
Porównanie η
lo = 2,96 m
As1 = As2 = 6,28 cm2
Λ = 29,10
k1=(fck/20)^(0,5)=(30/20)^(0,5) = 1,22
n=Ned/(Ac*fcd) = 1555,78 / ( 35 ^ 2 * 20 / 10 ) = 0,64
k2 = min ( n * Λ / 170; 0,2 ) = min ( 0,64 * 29,10 / 170; 0,2 ) = 0,109
φeff = 1,6
kc=k1*k2/(1+φeff) = 1,22 * 0,109 / ( 1+ 1,6) = 0,051
Ecm = 32 Gpa
Ecd = Ecm / γce = 32 / 1,2 = 27 Gpa
Jc = b*h^3 /12 = 35 * 25 ^ 3 / 12 = 125052 cm4
kc*Ecd*Jc = 0,051 * 27 * 125052 / 0,01^4 = 1635,90 m4
Js=As1*(0,5*h-a1)^2+As2*(0,5*h-d2)^2 = 6,28 *(0,5 * 35 - 4,8)^2+6,28 *(0,5*35-4,8) = 2025,80 cm4
Es = 200 GPa
Es*Js = 200 * 2025,80 0,01^4 = 4051,60 kNm2
E*J=kc*Ecd*Jc+Es*Js = 1709,71+ 4051,60 = 5687,51 kNm2
Nb=3,14^2*E*J/(lo^2) = 3,14^2*5687,51/(2,96^2) = 6406,76 kN
η = 1 / ( 1- Ned / Nb ) = 1 / ( 1 - 1555,78 / 6406,76 ) = 1,321
wielkość przyjęta do obliczania zbrojenia η = 1,3
bład (1,321 - 1,3 ) / 1,321 *100 = 1,64 % < 10 % warunek spełniony
Resztę przypadków przedstawiono w tabeli.
|
|
m |
lo |
= |
2,96 |
2,96 |
2,96 |
2,96 |
2,96 |
2,96 |
2,96 |
2,96 |
|
|
cm2 |
As1 |
= |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
|
|
cm2 |
As2 |
= |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
smukłość słupa |
|
- |
Λ |
= |
29,10 |
29,10 |
29,10 |
29,10 |
29,10 |
29,10 |
29,10 |
29,10 |
k1=(fck/20)^(0,5) |
|
- |
k1 |
= |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
n=Ned/(Ac*fcd) |
|
- |
n |
= |
0,79 |
0,65 |
0,79 |
0,65 |
0,82 |
0,67 |
0,82 |
0,67 |
k2=min(n*Λ/170;0,2) |
|
- |
k2 |
= |
0,136 |
0,112 |
0,136 |
0,112 |
0,141 |
0,115 |
0,141 |
0,115 |
|
|
- |
φeff |
= |
1,6 |
1,6 |
1,6 |
1,6 |
1,6 |
1,6 |
1,6 |
1,6 |
kc=k1*k2/(1+φeff) |
|
- |
kc |
= |
0,052 |
0,043 |
0,052 |
0,043 |
0,054 |
0,044 |
0,054 |
0,044 |
|
|
Gpa |
Ecm |
= |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
|
|
- |
γce |
= |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
|
|
Gpa |
Ecd |
= |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
Jc=b*h^3/12 |
|
cm4 |
Jc |
= |
125052 |
125052 |
125052 |
125052 |
125052 |
125052 |
125052 |
125052 |
kc*Ecd*Jc |
|
kNm2 |
kc*Ecd*Jc |
= |
1635,90 |
1347,10 |
1635,90 |
1347,10 |
1692,02 |
1383,81 |
1692,02 |
1383,81 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Js=As1*(0,5*h-a1)^2+As2*(0,5*h-d2)^2 |
|
cm4 |
Js |
= |
2025,80 |
2025,80 |
2025,80 |
2025,80 |
2025,80 |
2025,80 |
2025,80 |
2025,80 |
|
|
kNm2 |
Es*Js |
= |
4051,60 |
4051,60 |
4051,60 |
4051,60 |
4051,60 |
4051,60 |
4051,60 |
4051,60 |
E*J=kc*Ecd*Jc+Es*Js |
|
kNm2 |
E*J |
= |
5687,51 |
5398,71 |
5687,51 |
5398,71 |
5743,63 |
5435,41 |
5743,63 |
5435,41 |
Nb=3,14^2*E*J/(lo^2) |
|
kN |
Nb |
= |
6406,76 |
6081,44 |
6406,76 |
6081,44 |
6469,97 |
6122,78 |
6469,97 |
6122,78 |
|
|
|
η |
= |
1,321 |
1,267 |
1,321 |
1,267 |
1,332 |
1,274 |
1,332 |
1,274 |
|
|
% |
bład |
= |
1,64 |
3,88 |
1,64 |
-2,51 |
2,43 |
-1,98 |
2,43 |
-1,98 |
Wyznaczenie nośności Mrd przyjętego zbrojenia
Wyznaczenie nośności Mrd przyjętego zbrojenia w przekroju głowicy w kierunku Y-Y dla kombinacji 1
Etot = 4,97 cm
ξeff = (Ned + As1 * fyd - As2 * fyd ) / ( b * d * fcd ) = (1557,80 + 6,28 * 356,52 - 6,28* 356,52 ) / ( 35 * 30,20 * 356,52 ) = 0,9211
2*a2/d = 2 * 4,8 / 30,2 = 0,32
ξeff,lim = 0,5
ξeff .lim< ξeff ≤ 1.0
0,5 < 0,9211 ≤ 1.0 dlatego Mrd obliczam ze wzoru:
ξeff = (Ned + ( 2/ ( 1 - ξeff,lim) - 1) * As1 * fyd - As2 * fyd )/ (b*d*fcd + 2/ ( 1 - ξeff,lim)*As1*fyd)=( 1557,80 + ( 2/ ( 1 - 0,53) - 1) * 6,28 * 356,52 - 6,28 * 356,52 )/ (35*30,2*20/10 + 2/ ( 1 -0,5)*6,28*356,52)=0,762
Mrd = b*d^2*ξeff*(1-0,5*ξeff)*fcd+As2*fyd*(d-d2)-(0,5*h-d2)*Ned = 35*30,20^2*0,762*(1-0,5*0,762)*16/10+0,762*356,52/10*(30,20-4,8)-(0,5*35-4,8)* 1557,80 = 112,40 kNm
Resztę przypadków przedstawiono w tabeli.
|
|
|
|
Głowica |
Podstawa |
||||||
|
|
|
|
Y-y |
Z-z ` |
Y-y |
Z-z |
||||
Dane |
|
|
|
komb1 |
komb2 |
komb1 |
komb2 |
komb1 |
komb2 |
komb1 |
komb2 |
fcd |
MPa |
fcd |
= |
16,00 |
16,00 |
16,00 |
16,00 |
16,00 |
16,00 |
16,00 |
16,00 |
fyd |
MPa |
fyd |
= |
434,78 |
434,78 |
434,78 |
434,78 |
434,78 |
434,78 |
434,78 |
434,78 |
ξeff,lim |
- |
ξeff,lim |
= |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
Ned |
|
Ned |
= |
1557,80 |
1282,79 |
1557,80 |
1282,79 |
1611,24 |
1317,74 |
1611,24 |
1317,74 |
Geometria |
cm |
b |
= |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
|
cm |
h |
= |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
35,00 |
|
cm |
a1 |
= |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
|
cm |
a2 |
= |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
4,80 |
|
cm |
d |
= |
30,20 |
30,20 |
30,20 |
30,20 |
30,20 |
30,20 |
30,20 |
30,20 |
|
|
|
|
|
|
|
|
|
|
|
|
Zbrojenie |
cm2 |
As1 |
= |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
|
cm2 |
As2 |
= |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
6,28 |
Mimośród |
cm |
etot |
= |
4,97 |
9,33 |
6,12 |
7,03 |
3,74 |
6,48 |
4,34 |
4,77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξeff = (Ned + As1 * fyd * κs - As2 * fyd ) / ( b * d * fcd ) |
|
|
= |
0,9211 |
0,7585 |
0,9211 |
0,7585 |
0,9527 |
0,7792 |
0,9527 |
0,7792 |
|
- |
2*a2/d |
= |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
Jeżeli ξeff ≤2a2/d |
|
|
|
|
|
|
|
|
|
|
|
Mrd=As1*fyd*(d − a2)+(0,5*h-a2)*Ned |
kNm |
Mrd |
= |
- |
- |
- |
- |
- |
- |
- |
- |
Jeżęli 2a2/d< ξeff ≤ ξeff .lim |
|
|
|
|
|
|
|
|
|
|
|
MRd = b*d^2*ξeff*(1-0,5*ξeff)*fcd+As2*fyd*(d-a2)-(0,5*h-a2)*Ned |
kNm |
Mrd |
= |
- |
- |
- |
- |
- |
- |
- |
- |
Jeżeli ξeff > ξeff,lim |
|
|
|
|
|
|
|
|
|
|
|
ξeff = (Ned + ( 2/ ( 1 - ξeff,lim) - 1) * As1 * fyd - As2 * fyd )/ (b*d*fcd + 2/ ( 1 - ξeff,lim)*As1*fyd) |
- |
|
= |
0,762 |
0,665 |
0,762 |
0,665 |
0,781 |
0,678 |
0,781 |
0,678 |
Jeżeli ξeff .lim< ξeff ≤ 1.0 |
|
|
|
|
|
|
|
|
|
|
|
Mrd = b*d^2*ξeff*(1-0,5*ξeff)*fcd+As2*fyd*(d-d2)-(0,5*h-d2)*Ned |
kNm |
Mrd |
= |
112,40 |
133,23 |
112,40 |
133,23 |
107,80 |
130,84 |
107,80 |
130,84 |
Jeżęli ξeff > 1.0 |
|
κs |
= |
|
|
|
|
|
|
|
|
ξeff = (Ned - As1 * fyd * κs - As2 * fyd ) / ( b * d * fcd ) |
- |
ξeff |
= |
- |
- |
- |
- |
- |
- |
- |
- |
Mrd = b*d^2*ξeff*(1-0,5*ξeff)*fcd+As2*fyd*(d-d2)-(0,5*h-d2)*Ned |
kNm |
Mrd |
= |
- |
- |
- |
- |
- |
- |
- |
- |
Sprawdzenie warunku na dwukierunkowe ściskanie
Sprawdzenie warunku na dwukierunkowe ściskanie w przekroju głowicy w kierunku Y-Y dla kombinacji 1
etot,z = 6,12 cm
etot,y = 4,97 cm
Ned = 1557,80 kN
Med,z = Ned * etot,z = 1557,80 * 6,12 / 100 = 95,41 kNm
Mrd,z = 112,40 kNm
Med,y = Ned * etot,y = 1557,80 * 4,97 / 100 = 77,42 kNm
Mrd,y = 112,40 kNM
ez = Med,z /Ned = 95,41 / 1557,80 =0,05m
ey = Med,y /Ned = 77,42 / 1557,80 = 0,06 m
ey / h = 0,06 / 0,35 = 0,17
ez / b = 0,05/ 0,35 = 0,14
Sprawdzenie warunków na II kierunkowe ściskanie
(ey / h) / ( ez / b ) = 0,17 / 0,14 = 1,23 < warunek niespełniony
( ez / b ) / (ey / h) = 0,14/ 0,17 = 0,81 < warunek niespełniony
Należy uwzględnic II kierunkowe ściskanie
Nrd = Ac * fcd + As * fyd = 35 * 35 * 16 / 10 + (4 * 3,14 / 356,52 / 10) = 1960,00 kN
Ned / NRd = 1557,80 / 1960,00 = 0,795 → a = 1,33
(Med,z/Mrd,z)^a = ( 95,41 / 112,40 ) ^ 1,26 = 0,32
(Med,y/Mrd,y)^a = ( 77,42 / 112,40 ) ^ 1,26 = 0,15
(Med,z/Mrd,z)^a + (Med,y/Mrd,y)^a = 0,32 + 0,15 = 0,43 < 1 warunek spełniony
Resztę przypadków przedstawiono w tabeli.
|
|
|
Głowica |
Podstawa |
||
|
|
|
Y-y |
Z-z ` |
Y-y |
Z-z |
cm |
etot,z |
= |
5,18 |
5,95 |
3,68 |
4,04 |
cm |
etot,y |
= |
4,21 |
8,42 |
3,17 |
5,49 |
kN |
Ned |
= |
1557,80 |
1282,79 |
1611,24 |
1317,74 |
kNm |
Med,z |
= |
80,74 |
76,31 |
59,22 |
53,19 |
kNm |
Mrd,z |
= |
90,07 |
118,05 |
84,29 |
114,66 |
kNm |
Med,y |
= |
65,51 |
107,96 |
51,02 |
72,29 |
kNm |
Mrd,y |
= |
90,07 |
118,05 |
84,29 |
114,66 |
- |
a |
= |
1,33 |
1,26 |
0,51 |
0,42 |
- |
(Med,z/Mrd,z)^a |
= |
0,31 |
0,32 |
0,44 |
0,35 |
- |
(Med,y/Mrd,y)^a |
= |
0,12 |
0,15 |
0,16 |
0,201 |
|
suma |
= |
0,43 |
0,472 |
0,609 |
0,551 |
Obliczenia dla stopy
Zestawienie obciążeń
Wyniki dla osi liczbowej (Y-Y) |
|||
|
Komb 1 |
Komb 2 |
Komb 3 |
M2 [kNm] |
-14,16 |
-39,36 |
18,46 |
T [kNm] |
-10,06 |
-26,44 |
11,58 |
N1 [kNm] |
-885,25 |
-745,26 |
-730,92 |
N2 [kNm] |
-921,22 |
-762,73 |
-748,40 |
Wyniki dla osi literowej (Z-Z) |
|||
|
Komb 1 |
Komb 2 |
Komb 3 |
M2 [kNm] |
-21,61 |
-22,00 |
-10,73 |
T [kN] |
-15,09 |
-15,53 |
-7,34 |
N1 [kN] |
-672,55 |
-537,53 |
-497,66 |
N2 [kNm] |
-690,02 |
-555,01 |
-515,14 |
|
|
|
|
Suma N1 [kN] |
-1557,80 |
-1282,79 |
-1228,58 |
Suma N2 [kN] |
-1611,24 |
-1317,74 |
-1263,54 |
Wymiary stopy fundamentowej
H = L = 2,5 m
hf = 50 cm = 0,5 m
Obliczenia dla komb 1
Ved = 1611,24 kN
Med,y = 14,16 kNm
Med,z = 21,61 kNm
Momenty z uwzględnieniem wpływu siły tnącej
Med,y' = Med,y + hf * Ty = 14,16 + 0,5 *10,06 = 19,19 kNm
Med,z' = Med,z + hf * Tz = 21,61 + 0,5 * 15,09 = 29,16 kNm
Naprężenia pod stopą
Wy = Wz = L * B ^ 2 / 6 = 2,5 * 2,5 ^ 2 / 6 = 2,6 m3
Ϭa = Ved / ( B * L ) - Med,y' / Wy - Med,y' / Wz = 1611,24 / ( 25, * 2,5 ) - 19,19 / 2,6 - 29,16 / 2,6 = 239,23 kN/m2
Ϭb = Ved / ( B * L ) + Med,y' / Wy - Med,y' / Wz = 1611,24 / ( 25, * 2,5 ) + 19,19 / 2,6 - 29,16 / 2,6 = 261,62 kN/m2
Ϭc = Ved / ( B * L ) + Med,y' / Wy + Med,y' / Wz = 1611,24 / ( 25, * 2,5 )+ 19,19 / 2,6 + 29,16 / 2,6 = 276,36 kN/m2
Ϭd = Ved / ( B * L ) - Med,y' / Wy+ Med,y' / Wz = 1611,24 / ( 25, * 2,5 ) - 19,19 / 2,6 + 29,16 / 2,6 = 253,97 kN/m2
Ϭś = 257,8 kN/m2 <= qf = 280 kN/m2 warunek spełniony
qmax = 276,36 kN/m2 <= 1,2 * qf = 1,2 * 280 = 336 kN/m2 warunek spełniony
Wyznaczenia zbrojenia na zginanie
Mz=Ϭśr*B*0,5*((L-cl)/2)^2=257,8 * 2,5 * 0,5 * (( 2,5 - 0,35 )/ 2 )^2 = 372,4 kNm
My=Ϭśr*L*0,5*((B-cb)/2)^2= 257,8 * 2,5 * 0,5 * (( 2,5 - 0,35 )/ 2 )^2 = 372,4 kNm
Asz = Mz / ( 0,9 * dz * fyd ) = 372,4 / ( 0,9 * 0,45 * 434,8 ) = 21,15 cm2
Asy = My / ( 0,9 * dy * fyd ) = 372,4 / ( 0,9 * 0,43 * 434,8 ) = 22,13 cm2
Asz/B = 21,15 / 2,5 = 8,46 cm2 / m
przyjeto ϕ12 co 12 cm Asz,prov = 9,42 cm2 / m
Asy/B = 22,13 / 2,5 = 8,85 cm2 / m
przyjeto ϕ12 co 12 cm Asz,prov = 9,42 cm2 / m
ρlz = Asz / ( B * dz ) = 9,42 / ( 2,5 * 0,45 ) = 0,00084
ρly = Asy / ( B * dy ) = 9,42 / ( 2,5 * 0,43 ) = 0,00088
ρ = (ρlz ^ 2 + ρly ^ 2 ) ^(0,5) = 0,00064
d= 0,5*(dz+dy)=0,5*(0,45+0,43)=0,44 m
Sprawdzenie przebicia w odległości 0,5 d od lica słupa
A = 0,5 * d = 0,5 * 0,44 = 0,22 m
Ul = 2*c1+2*c2+3,14*d = 2*(0,35 + 0,35) + 3,14 * 0,44 = 2,78 m
As,l = c1 * c2 + (c2 +c1 ) * d + 3,14 * d^2 / 4 = 0,45 * 0,45 + (0,45 + 0,45 ) * 0,44 + 3,14 * 0,44 ^2 / 4 = 0,58 m2
Ved,req = Ved - Ϭś * As,l = 1611,24 - 257,8 * 0,58 = 1461,06 kN
ey = Med,y / Ved,req = 14,16 / 1461,06 = 0,0097 m
ez = Med,z / Ved,req = 21,61 / 1461,06 = 0,0148 m
bz = c1 + d = 0,35 + 0,44 = 0,79 m
by = c2 + d = 0,35 + 0,44 = 0,79 m
β=1+1,8*((ey/bz)^2+(ez/by)^2)^(0,5) = 1+1,8*((0,0097/0,79)^2+(0,0148/0,79)^2)^(0,5) = 1,040
Ved=β*Ved,req/(Ul * d) = 1,040 * 1461,06 /( 2,78 * 0,44 ) = 1,24 MPa
CR,d = 0,12
k = 1+ ( 200 / d ) ^ (0,5 ) = 1+ ( 200 / 440 ) ^ (0,5 ) = 1,67
Vrd,c = CR,d * k * ( 100 * ρ *fck ) ^ (1/3) * 2 * d / a = 0,12 * 1,67 * ( 100 * 0,00064 * 30 ) ^ (1/3) * 2 * 0,44 / 0,22 = 1,101 MPa
vmin = 0,035 * k ^ ( 3/2) * fck ^ ( ½) = 0,035 * 1,67 ^ ( 3/2) * 30 ^ ( ½) = 0,4153 MPa
Vrd,min = vmin * 2 * d / a = 0,4153 * 2 * 0,44 / 0,2 = 1,6611 MPa
Vrd,c = 1,101 MPa > Vrd,min = 1,6611 MPa
Vrd,c = 1,6611 MPa
Ved = 1,24 MPa < Vrd,c = 1,6611 MPa warunek spełniony
Sprawdzenie przebicia w odległości 2 d od lica słupa
a = 2 * d = 2 * 0,44 = 0,88 m
ul = 2 * ( c1 + c2 ) + 2 * 3,14 * 2 * d / 2 = 2 * ( 0,35 + 0,35 ) + 2 * 3,14 * 2 * 0,44 / 2 = 4,16 m
As,l = c1 * c2 + 2 * d * ( c1 + c2 ) + 3,14 * ( 2 * d ) ^ 2 = 0,35 * 0,35 + 2 * 0,44 * ( 0,35 + 0,35 ) + 3,14 * ( 2 * 0,44 ) ^ 2 = 3,79 m2
Ved,req = Ved - Ϭś * As,l = 1611,24 - 257,8 * 3,79 = 634,87 kN
ey = Med,y / Ved,req = 14,16 / 634,87 = 0,0223 m
ez = Med,z / Ved,req = 21,61 / 634,87 = 0,0340 m
bz = c1 + 2*d = 0,35 + 2 * 0,44 = 1,14 m
by = c2 + 2* d = 0,35 + 2 * 0,44 = 1,14 m
β=1+1,8*((ey/bz)^2+(ez/by)^2)^(0,5) = 1+1,8*((0,0223/1,14 )^2+(0,0340/1,14 )^2)^(0,5) = 1,064
Ved=β*Ved,req/(Ul * d) = 1,064 * 634,87/( 4,16* 0,44 ) = 0,37 MPa
CR,d = 0,12
k = 1+ ( 200 / d ) ^ (0,5 ) = 1+ ( 200 / 440 ) ^ (0,5 ) = 1,67
Vrd,c = CR,d * k * ( 100 * ρ *fck ) ^ (1/3) * 2 * d / a = 0,12 * 1,67 * ( 100 * 0,00064 * 30 ) ^ (1/3) * 2 * 0,44 / 0,88 = 0,275 MPa
vmin = 0,035 * k ^ ( 3/2) * fck ^ ( ½) = 0,035 * 1,67 ^ ( 3/2) * 30 ^ ( ½) = 0,4153 MPa
Vrd,min = vmin * 2 * d / a = 0,4153 * 2 * 0,44 / 0,88 = 0,4153 MPa
Vrd,c = 0,275 MPa > Vrd,min = 0,4153 MPa
Vrd,c = 0,4153 MPa
Ved = 0,37 MPa < Vrd,c = 0,4153 MPa warunek spełniony
Resztę przypadków przedstawiono w tabeli.
|
|
|
Przebicie w odl. 0,5 d |
Przebicie w odl. 2 d |
||
|
|
|
komb1 |
komb2 |
komb1 |
komb2 |
kPa |
qf |
= |
280 |
280 |
280 |
280 |
m |
B |
= |
2,5 |
2,5 |
2,5 |
2,5 |
m |
L |
= |
2,5 |
2,5 |
2,5 |
2,5 |
Mpa |
fyd |
= |
434,8 |
434,8 |
434,8 |
434,8 |
Mpa |
fcd |
= |
20 |
20 |
20 |
20 |
- |
ksilim |
|
0,5 |
0,5 |
0,5 |
0,5 |
m |
dz |
= |
0,45 |
0,45 |
0,45 |
0,45 |
Mpa |
dy |
= |
0,43 |
0,43 |
0,43 |
0,43 |
m |
c1 |
= |
0,35 |
0,35 |
0,35 |
0,35 |
m |
c2 |
= |
0,35 |
0,35 |
0,35 |
0,35 |
m3 |
Wz |
= |
2,6 |
2,6 |
2,6 |
2,6 |
m3 |
Wy |
= |
2,6 |
2,6 |
2,6 |
2,6 |
kNm |
Med,y |
= |
14,16 |
39,36 |
14,16 |
39,36 |
kNm |
Med,z |
|
21,61 |
22 |
21,61 |
22 |
kN |
Ned |
= |
1611,24 |
1317,74 |
1611,24 |
1317,74 |
Mpa |
fck |
= |
30 |
30 |
30 |
30 |
m |
hf |
= |
0,5 |
0,5 |
0,5 |
0,5 |
kN |
Ty |
= |
10,06 |
26,44 |
10,06 |
26,44 |
|
Tz |
= |
15,09 |
15,53 |
15,09 |
15,53 |
kNm |
Med,y' |
= |
19,19 |
52,58 |
19,19 |
52,58 |
kNm |
Med,z' |
= |
29,16 |
29,77 |
29,16 |
29,77 |
|
|
|
|
|
|
|
kN/m2 |
Ϭa |
= |
239,23 |
179,22 |
239,23 |
179,22 |
kN/m2 |
Ϭb |
= |
261,62 |
202,08 |
261,62 |
202,08 |
kN/m2 |
Ϭc |
= |
276,36 |
242,46 |
276,36 |
242,46 |
kN/m2 |
Ϭd |
= |
253,97 |
219,6 |
253,97 |
219,6 |
kN/m2 |
Ϭśr |
= |
257,8 |
210,84 |
257,8 |
210,84 |
|
|
|
|
|
|
|
|
qmax |
= |
276,36 |
242,46 |
276,36 |
242,46 |
|
1,2*qf |
= |
336 |
336 |
336 |
336 |
|
|
|
|
|
|
|
kNm |
Mz |
= |
372,4 |
304,56 |
372,4 |
304,56 |
kNm |
My |
= |
372,4 |
304,56 |
372,4 |
304,56 |
cm2 |
As,z |
= |
21,15 |
17,3 |
21,15 |
17,3 |
cm2 |
As,y |
= |
22,13 |
18,1 |
22,13 |
18,1 |
cm2/m |
As,z/B |
= |
8,46 |
6,92 |
8,46 |
6,92 |
cm2/m |
As,y/L |
= |
8,85 |
7,24 |
8,85 |
7,24 |
cm2 |
As,z,prov |
= |
9,42 |
9,42 |
9,42 |
9,42 |
cm2 |
As,y,prov |
= |
9,42 |
9,42 |
9,42 |
9,42 |
- |
ρlz |
= |
0,00084 |
0,00084 |
0,00084 |
0,00084 |
- |
ρly |
= |
0,00088 |
0,00088 |
0,00088 |
0,00088 |
|
ρl |
= |
0,00086 |
0,00086 |
0,00086 |
0,00086 |
|
|
|
|
|
|
|
m |
d |
= |
0,44 |
0,44 |
0,44 |
0,44 |
|
|
|
|
|
|
|
m |
a |
= |
0,22 |
0,22 |
0,88 |
0,88 |
m |
ul |
= |
2,78 |
2,78 |
4,16 |
4,16 |
m2 |
As,l |
= |
0,58 |
0,58 |
3,79 |
3,79 |
kN |
Ved,req |
= |
1461,06 |
1194,92 |
634,87 |
519,22 |
m |
ey |
= |
0,0097 |
0,0329 |
0,0223 |
0,0758 |
m |
ez |
= |
0,0148 |
0,0184 |
0,0340 |
0,0424 |
|
bz |
= |
0,79 |
0,79 |
1,14 |
1,14 |
|
by |
= |
0,79 |
0,79 |
1,14 |
1,14 |
|
β |
= |
1,040 |
1,086 |
1,064 |
1,137 |
Mpa |
Ved |
= |
1,24 |
1,06 |
0,37 |
0,32 |
|
|
|
|
|
|
|
|
Crd |
= |
0,12 |
0,12 |
0,12 |
0,12 |
|
k |
= |
1,67 |
1,67 |
1,67 |
1,67 |
|
|
|
|
|
|
|
Mpa |
Vrd,c |
= |
1,101 |
1,101 |
0,275 |
0,275 |
Mpa |
vmin |
= |
0,4153 |
0,4153 |
0,4153 |
0,4153 |
Mpa |
Vrd,min |
= |
1,6611 |
1,6611 |
0,4153 |
0,4153 |
PG WILIŚ |
Bartłomiej Wiater indeks 132955 Słup + Stopa |
5 |
Wyszukiwarka
Podobne podstrony:
Modelowanie w Robocie (płyta słup)(1)
4 Słup jednokier przykład NS ukl o wezl nieprzes
04 HBT Slup EC3
06 slup teoria
słup soli, lektury
7 Słup
Projekt 2 Plyta Slup Guide cz II
Mathcad SŁUP PROJEKT 23 05
K 08 SLUP id 229567 Nieznany
Tajemniczy słup światła nad piramidą Chichen Itza, W ஜ DZIEJE ZIEMI I ŚWIATA, ●txt RZECZY DZIWNE
slup uzwojony
słup
Metale słup
WĘZŁY słup 2, Skrypty, PK - materiały ze studiów, II stopień, pomoc, III semestr, Konstrukcje stalow
wyniki słup srodkowy
Słup żelbetowy poprawiony
projekt cz2 slup
SŁUP DWUTEOWY KLEJONY, SŁUP DWUTEOWY KLEJONY
Instrukcja K1, 53-68, Słup kilometrowy
więcej podobnych podstron