1. Co to jest transmitancja operatorowa?

Transmitancja operatorowa - stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego przy zerowych warunkach początkowych.

2. Jak przenosi się węzeł sumacyjny z wejścia elementu na wyjście.

3.Jak się przenosi węzeł sumacyjny w wyjścia elementu na wejście?

4. Podać transmitancje wypadkową układu zamkniętego z dodatnim sprzężeniem zwrotnym w postaci ogólnej.

5. Podać transmitancje wypadkową układu zamkniętego z ujemnym sprzężeniem zwrotnym w postaci ogólnej.

6. Co oznacza w kryterium Hurwitza ∆_n=0?

∆_n=0 - wyznacznik główny kryterium Hurwitza jest równy 0, co oznacza, że układ znajduje się na granicy stabilności. (Kryterium Hurwitza stanowi warunek wystarczający stabilności układu).7. Omówić sposób postępowania w przypadku wiersza zerowego w tablicy Routha.

Wiersz leżący bezpośrednio nad nim podaje współczynnik czynnika parzystego s⁴+4s²+4 aby obliczyć niższe współczynniki tablicy Routha zastępujemy wiersze ze współczynnikami pochodnej czynnika parzystego

9. Podać kryterium Michajłowa i narysować przebieg M(jω) dla układu na granicy stabilności.

Układ automatycznej regulacji (UAR) jest stabiny jeżeli przyrost argumentu wyrażenia M(jω) (wielomianu Michajłowa) przy zmianach pulsacji od -∞ do +∞ jest rowny n∙π, czyli ∆argM(jω)= n∙π i ω€(-∞,+∞)

Przebieg M(jω) dla układu na granicy stabilności - M(jω)= U(ω)+jV(ω)

10.Podać kryterium Michajłowa i jego interpretację na podstawie przebiegu charakterystyk Re{M(jω)}i Im{M(jω)}

UAR jest stabilny, jeżeli przy zmianach pulsacji od 0 do ∞ charakterystyka M(jω) będzie przechodziła przez n ćwiartek płaszczyzny w dodatnim kierunku trygonometrycznym.

11.Podać postać kryterium Nyquista dla układów astatycznych

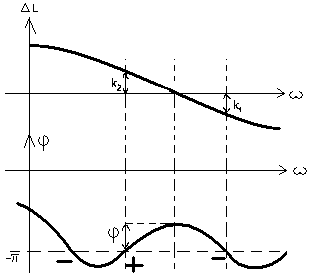
12. Wyjaśnić pojęcie zapasu stabilności amplitudy za pomocą charakterystyk logarytmicznych.

-Dla przejścia „ujemnego”: 1/k₁ jest zapasem stabilności amplitudy

-Dla przejścia „dodatniego”: 1/k2 jest zapasem stabilności amplitudy.

-φ jest kątem nazywanym zapasem stabilności fazy

Przebiegi przykładowe

13. Podać kryterium Nyquista dla niestabilnego układu otwartego (wariant z przyrostem argumentu).

Równanie charakterystyczne układu zamkniętego ma wszystkie pierwiastki w LPP zmiennej zespolonej s przy założeniu, że równanie układu otwartego ma m pierwiastków w PPP wtedy i tylko wtedy, gdy przyrost argumentu wyrażenia 1+G₀(jω) przy zmianach ω od -∞ do +∞ wynosi 2πm, czyli:

(niestab. Układ otwarty)

14. Podać kryterium Nyquista dla stabilnego układu otwartego (wariant z przyrostem argumentu).

Równanie charakterystyczne układu zamkniętego ma wszystkie pierwiastki w LPP zmiennej zespolonej s przy założeniu, że równanie układu otwartego ma wszystkie pierwiastki w LPP wtedy i tylko wtedy, gdy przyrost argumentu wyrażenia 1+G₀(jω) przy zmianach ω od -∞ do +∞ wynosi 0, czyli:

(stab. Układ otwarty)

15. Podać kryterium Nyquista dla stabilnego układu otwartego (wariant z charakterystyką amplitudowo-fazową).

Zamknięty UAR jest stabilny przy założeniu, że układ otwarty jest stabilny wtedy i tylko wtedy, gdy charakterystyka amplitudowo-fazowa układu otwartego G₀(jω) przy zmianach ω od -∞ do +∞ nie obejmuje punktu (-1, j0). (stabilny układ otwarty)

16. Podać kryterium Nyquista dla stabilnego układu otwartego (wariant z charakterystykami loagarytmicznymi).

Zamknięty UAR jest stabilny przy założeniu, że układ otwarty jest stabilny wtedy i tylko wtedy, gdy dla wszystkich pulsacji ω od 0 do +∞ dla których L(ω)≥0, liczba dodatnich przejść krzywej φ(ω) przez prostą -π jest równa liczbie przejść ujemnych.

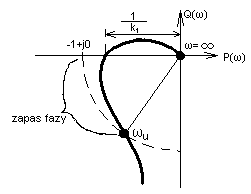
17. Wyjaśnić pojęcie zapasu stabilności amplitudy i fazy za pomocą charakterystyk amplitudowo-fazowych.

Sposób postępowania: rysujemy okrąg o promieniu 1 (czyli przechodzący przez punkt -1+j0) o środku w punkcie (0,0). Okrąg ten przecina daną charakterystykę w punkcie ωu. Rysujemy odcinek łączący początek układu współrzędnych z punktem ωu. Kąt wyznaczony między ujemną częścią od P(ω) i narysowanym odcinkiem nazywamy zapasem fazy. Odległość punktu przecięcia charakterystyki z osia P(ω) od początku układu współrzędnych nazywamy zapasem stabilności amplitudy.
18. Wyjaśnić pojęcie zapasu stabilności amplitudy i fazy za pomocą charakterystyk logarytmicznych.

PARTZ PYTANIE 12

19. Wymienić rodzaje kryteriów jakości UAR.

Rodzaje kryteriów jakości UAR:

-dokładność w stanie ustalonym,

-dokładność w stanie przejściowym (szybkość działania UAR),

-kryteria zapasu stabilności (fazy i amplitudy),

-kryteria całkowe.

20. Uzasadnić twierdzenie, że wzrost współczynnika wzmocnienia układu otwartego poprawia jakość w stanie ustalonym.

Wzrost współczynnika wzmocnienia układu otwartego poprawia jakość w stanie ustalonym, ponieważ zmniejsza się wtedy uchyb ε_ust(s):

Gdzie G_u - transmitancja uchybowa, y₀ - zadany sygnał

(dla sygnału jednostkowego)

G₀ - współczynnik zerowy uchybu, k₀ - wzmocnienie

21. Dlaczego podnoszenie stopnia astatyzmu zwiększa dokładność w stanie ustalonym?

Podnoszenie stopnia astatyzmu zwiększa dokładność w stanie ustalonym: εust dla

w układzie astatycznym rzędu r dla q≤r-1 uchyb:

gdzie M_otw1 - mianownik dla ukł otwartego

24.Wymienić sposoby poprawiania jakości UAR w stanie ustalonym

-zwiększenie współczynnika wzmocnienia ukł.otwartego

-zwiększenie rzędu astatyzmu układu

-zmiana stałej różniczkowania Tp(sterowanie z użyciem różniczek uchybu)

(sterowanie z użyciem pochodnych uchybu)

25.omówić sposoby poprawiania jakości układu przez podnoszenie stopnia astatyzmu(patrz pyt.21)

26.wymienić sposoby poprawiania jakości UAR za pomocą sterowania z użyciem pochodnych uchybu:

Współczynnik uchybu G_Z w wyniku różniczkowania uchybu ma mniejszą wartość od współczynnika w ukł. Bez różniczkowania.Stosowanie różniczkowania zwiększa zwykle zapas stabilności układu.

29.wyjaśnic pojecie współczynnika oscylacji:

31.co to jest oscylacja?
,gdzie s_i=sprzężone pierwiastki zespolone
;
-przeregulowanie

32.co to jest układ astatyczny?def.1-ukł.w którego torze głównym występuje człon całkujący(lub wiele członów połączonych w szereg)

Def.2-ukł,w którym transmitancja dla ukł.otwartego ma biegun w początku ukł. Współrzędnych

34.do czego służą okręgi stałej amplitudy?-służą do wyznaczania transmitancji ukł. Zamkniętego,a także współczynnika oscylacji i pulsacji

-srodek okregu:
- promień okręgu R=

35.podac transmitancje i narysować charakterystyki logarytmiczne korektora przyspieszającego fazę

Transmitancje:

36.podac transmitancje i odpowiedz korektora opóźniającego fazę.narysować ten przebieg.

Odpowiedz-

38.Narysować charakterystyki logarytmiczne regulatora PD.

39. Narysować charakterystyki logarytmiczne regulatora PID.

40. Narysować charakterystyki logarytmiczne regulatora PI.

41.Narysować h(t) regulatora PI.

Odpowiedź jednostkowa regulatora PI:

42.Wyjaśnić znaczenie stałej T_d regulatora PD za pomocą odpowiedniego rysunku.

odpowiedź:

Czas, o który część różniczkująca k_pT_D wyprzedza część proporcjonalną k_p nazywamy czasem T_D.

43. Wyjaśnić znaczenie stałej T_i regulatora PI za pomocą odpowiedniego rysunku.

Czas zdwojenia T_i - to czas, po którym przebieg osiagnie wartość 2k_p

44.Wymienic podstawowe rodzaje regulatorów.

(1)ze względu na sposób zasilania reg. w energię potrzebną do pracy - reg. działania bezpośredniego

(2)w zależności od rodzaju nośnika energii pomocniczej - elektryczne,hydrauliczne,pneumatyczne,mechaniczne,kombinowane- reg. działania pośredniego

(3)ze względu na postać transmitancji operatorowej - proporcjonalne P,całkowe I,proporcjonalno-całkowe PI,proporcjonalno-różniczkowe-PD,prop.-całk.-różn.-PID

45.Wymienić rodzaje korektorów z punktu widzenia ich właściwości dynamicznych.

(1)opóźniający fazę

(2)przyspieszający fazę

(3)opóźniająco-przyspieszający

47.Podać wzór na transformatę splotu funkcji.

,gdzie

49)Podać wzór na przeksz. odwrotne trans. Laplace'a dla pierw. wielokrotnych rów. charakt.

f(t)= L
{F(s)}=

.

50)Podać wzór na trans. Funkcji
.

.

51)Transmitancja wypad. połączenia równ. Elementów.

.

52)Podać wzór na transf. Laplace'a fun. t*1(t).

.

53) Podać wzór na transf. Laplace'a fun.
.

.

54)Omówić sposób przenosz. węzła sum. sprzed bloku za blok.

y(s)=G(s)(u(s) x(s))

y(s)= G(s)u(s) G(s)x(s) =G(s)(u(s) x(s))

55)Jak wyznaczyć odp. układu na dowolny syg. mając odp. g(t)?

Należy obliczyć transmitancję Laplace'a- L{g(t)}.Otrzymujemy g(s), czyli odp. impulsową, która jest równa transmitancji G(s): g(s)=G(s). Następnie liczymy odp.: jednostkową
i L
{h(s)}=h(t), na impuls narastający liniowo h(s)=
i L
{h(s)}=h(t).

56)Podać przykład elementu całkującego rzeczywistego i jego transmitancje.

El. całkujący pierwszego rzędu - czwórnik RC

57) Podać przykład elementu oscylacyjnego i jego transmitancje.

El. oscylacyjny-czwórnik RLC

58.Element różniczkujący rzeczywisty:

przykład: czwórnik RC:

, T=RC

59.El całkujący rzeczywisty: równanie i transmitancja

60.El. oscylacyjny: rów. i transmitancja

ω₀-pulsacja drgań nietłumionych

ζ-wzg. Współczynnik tłumienia

k-współczynnik wzmocnienia(proporcjonalności)

61.El. różniczkujący rzeczywisty:

62.Przykładowa char. Amplitudowo-fazowa na płaszczyźnie Black'a

element różniczkujący z inercją-

63.Wzór na odpowiedź impulsową elementu całkującego rzeczywistego w funkcji czasu:

64.Wz. na odp. imp. el. oscylacyjnego w f. Czasu:

65.Wz. na odp. imp. El. Inercyjnego II rzędu w f. Czasu

66.Wz. na odp. jednostkową el. Oscylacyjnego:

66. Wzór na odpowiedź jednostkową elementu oscylacyjnego

67. Wzór na odpowiedź jednostkową elementu różniczkującego rzeczywistego.

68. Wzór na odpowiedź jednostkową elementu całkującegorzeczywistego w funkcji czasu. Narysować przebieg.

69. Podać równanie i transmitancję elementu inercyjnego II rzędu.

^ delta≥0

70. Postać wykładnicza transmitancji widmowej elem. całkującego rzeczywistego. Przebieg charakterystyki amplitudowo-fazowej.

71. Postać wykładnicza transmitancji widmowej elem. różniczkującego rzeczywistego. Przebieg charakterystyki amplitudowo-fazowej.

72. Postać wykładnicza transmitancji widmowej elem. inercyjnego II rzędu. Przebieg charakterystyki amplitudowo-fazowej.

74. Postać wykładnicza transmitancji widmowej elem. oscylacyjnego. Przebieg charakterystyki amplitudowo-fazowej.

76. Wzór na odpowiedź jednostkową elementu inercyjnego II rzędu.

77. Charakterystyki logarytmiczne elementu całkującego rzeczywistego.

78. Charakterystyki logarytmiczne elementu inercyjnego.

79. Charakterystyki logarytmiczne elementu inercyjnego 2 rzędu.

80.Charakterystyki logarytmiczne elementu różniczkującego rzeczywistego

81. Charakterystyki logarytmiczne elementu oscylacyjnego.

82. Charakterystyki logarytmiczne elementu opóźniającego.

83. Wyznaczyć wartość końcową h(t) elementu inercyjnego 2 rzędu za pomocą twierdzeń o wartościach granicznych.

G(s) = k / (sT₁+1)(sT₂+1)

h(s) = k / s(sT₁+1)(sT₂+1)

h(∞) = lim sh(s) = k (s->0)

h(0) = lim sh(s) = 0 (s->∞)

88. Sposób wyznaczania liczby pierwiastków równania charakt. W prawej półpłaszczyźnie zmiennej zespolonej s (w PPP) za pomocą kryterium Hurwitza.

L_ppp=V[a_n, Δ₁, Δ₁/Δ₂, Δ₂/ Δ₃, … , Δ_n/ Δ_n-1] = V[a_n, Δ₁, Δ₃, …] + V[1, Δ₂, Δ₄, …]

Ilość zmian znaku argumentów funkcji V decyduje o ilości pierwiastków w PPP, np. jeśli występują dwie zmiany znaku, to ONZ ze istnieją 2 pierwiastki w PPP.

89. Sposób wyznaczania liczby pierwiastków równania charakterystycznego w PPP za pomocą kryterium Michajłowa.

Δarg M(jω) = (n-2m) gdzie n- stopień równ.charakt. m≠0 →ukł.niestabilny

Δarg M(jω) = -π → -π = (3 - 2k)π → -π = 3π -2kπ → k = 2 - dwa pierwiastki w PPP.

94.Podać transmitancję wypadkową układu zamkniętego z dodatnim sprzężeniem zwrotnym w postaci ogólnej.

G(s) = y(s) / u(s) = G₁(s) / (1- G₁(s) G₂(s))

46. Wymienić rodzaje korektorów z punktu widzenia ich położenia w układzie.

Człony korekcyjne włącza się często szeregowo w tor główny regulacji. Korekcja może także polegać na włączeniu dodatkowych członów w tor sprzężenia zwrotnego obejmującego wybrany człon lub zespół członów albo rzadziej na włączeniu członów równolegle z wybranym elementem.

48. Podać wzór na przekształcenie odwrotne transformaty Laplace'a dla pierwiastków pojedynczych równania charakterystycznego.

84. Wyznaczyć wartość końcową g(t) elementu całkującego rzeczywistego za pomocą twierdzeń o wartościach granicznych.

85. Wyznaczyć wartość końcową h(t) elementu różniczkującego rzeczywistego za pomocą twierdzeń o wartościach granicznych.

86. Wyznaczyć wartość początkową h(t) elementu oscylacyjnego za pomocą twierdzeń i wartościach granicznych.

92. Sposób wyznaczania liczby pierwiastków równania charakterystyczngo w PPP z kryterium Routha.

Liczba pierwiastków znajdujących się w PPP jest równa liczbie zmian znaku wyrażeń w pierwszej kolumnie tablicy Routha.

8. Omówić sposób postępowania w przypadku elementu zerowego w tablicy Routha.

W przypadku wystąpienia elementu zerowego w tablicy Routha podstawiamy w miejsce zera
.

7. Omówić sposób postępowania w przypadku wiersza zerowego w tablicy Routha.

Wiersz leżący bezpośrednio nad nim podaje współczynnik czynnika parzystego s⁴+4s²+4 aby obliczyć niższe współczynniki tablicy Routha zastępujemy wiersze ze współczynnikami pochodnej czynnika parzystego.

27. Uzasadnić wniosek, że podnoszenie rzędu astatyzmu może spowodować niestabilność. Jaka to niestabilność?

Jest to niestabilność strukturalna przy układzie otwartym o transmitacji:

dokładność wzrasta ale układ jest niestabilny, ponieważ przy s nie ma współczynnika. Brak współczynnika wymaga zmiany struktury układu aby osiągnąć stabilność.

30. Podać przykład transmitancji układu astatycznego II rzędu.

37. Omówić pojęcie stopnia stabilności.

Stopień stabilności µ definiowany jest jako:

Stopień stabilności mówi nam o szybkości zanikania składowej przemiennej.

92. Sposób wyznaczania liczby pierwiastków równania charakterystycznego PPP za pomocą kryt. Routha.

Liczba pierwiastków znajdujących się w PPP jest równa liczbie zmian znaku wyrażeń w pierwszej kolumnie tablicy Routha.

---