Ćwiczenia 4

Zadanie 1.

Na podstawie danych z lat 1990 - 2006 oszacowano model ekonometryczny postaci

y_t = 200 +18x_1t +10x_2t , t = 1, 2, …, 17.

Oszacowana wariancja składnika losowego wynosi S² = 331, a macierz kowariancji

estymatorów jest równa

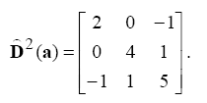
Ponadto znane są trendy zmiennych objaśniających dla t = 1, 2, …, 17:

x_1t = 6 + 0,2t , x_2t = 20 + 0,5t .

Przy założeniu, że składniki losowe modelu opisującego zmienną y mają rozkład normalny

N(0, σ2) oraz przyjmując poziom wiarygodności 0,9 wyznacz prognozę punktową i

przedziałową zmiennej y na rok 2009.

Zadanie 2.

Oszacowano model postaci y_t = 4+ 2x_1t +3x_2t- 5x_3t , t = 1, 2, …, 30.

Wariancja składnika losowego S² = 20, a macierz kowariancji estymatorów jest równa

D²(a) =

Trendy zmiennych objaśniających dla t= 1, 2, ..., 30

x_1t = 3t , x_2t = 0,25t² , x_3t = 2t + 3.

1. Przyjmując poziom wiarygodności 0,95 wyznacz prognozę punktową i przedziałową dla okresu t=32

2. Wyznacz średni błąd predykcji ex ante

3. Wyznacz średni błąd szacunku parametru przy zmiennej x₁

4. Wyznacz średni błąd szacunku wyrazu wolnego

Zadanie 3.

Oszacowano model postaci y_t = 10 - 2x_1t t = 1, 2, …, 30.

Błąd standardowy reszt wynosi 3.

Macierz

(X^TX)^-1 =

Przyjmują poziom wiarygodności 90% podaj prognozę punktową i przedziałową dla okresu t=40, jeśli x₁ w okresie t=40 wyniesie 3

Zadanie 4

W wyniku estymacji parametrów modelu

ekonometrycznego dokonanej na podstawie próby rocznej za lata 1980 - 2002 otrzymano:

Y_t =1+ 2X_1t − 2X_2t

Wiadomo także, iż oszacowanie wariancji składnika losowego wyniosło 1, wszystkie

parametry oszacowano z dokładnością do ± , a kowariancje między estymatorami

parametrów były następujące:

cov( α0 , α1 ) ) = -0,4, cov( α0 , α2 ) ) = -0,4, cov( α1 , α2 ) ) = 0,1.

Jakiej wartości zmiennej objaśnianej należy oczekiwać w roku 2003, jeśli wiadomo, że

zmienna X2t przyjmie wartość 1, natomiast zmienność X1t jest bardzo dobrze objaśniana przez

model postaci

X_1t = 8 − 0,5t , gdzie t = -11, …, 11.

Parametry powyższego modelu również oszacowano na podstawie próby rocznej za lata 1980

- 2002. Nie ma przesłanek do przypuszczenia, by tendencja ta miała ulec zmianie.

Wyznacz błąd prognozy ex ante i dokonaj prognozy przedziałowej zmiennej Y na rok 2003.

Zadanie 5

Przeciętne emerytury i renty w Polsce w latach

Źródło: Rocznik Statystyczny GUS 1993.

a) Aproksymując trend przeciętnych miesięcznych emerytur i rent, przyjmij funkcję

wykładniczą.

b) Jakiej wysokości przeciętnych rent i emerytur można się spodziewać w latach 1993 i 1994?

Podaj średnie błędy predykcji ex ante.

Zadanie 6

Na podstawie danych z lat 1992 - 2006 oszacowano dwa liniowe modele ekonometryczne

opisujące kształtowanie się ilości ścieków oczyszczanych w oczyszczalni NIDA S.A. w

Zmyślu (ILO, mln m3; dane w pliku [oczyszczalnia_sciekow.xls]):

(I) model trendu liniowego:

ILOt = 27,93 - 0,89⋅t, t = 1, 2, … 15.,

(II) model, w którym zmienną objaśniającą jest ilość zużytej energii elektrycznej ELE (mln

kWh):

ILOt = 90,64 - 7,50⋅ELEt.

a) Wyznacz prognozy wewnątrz próby na lata 2003 - 2006 dla obu modeli.

b) Oblicz i zinterpretuj następujące miary predykcji ex post dla okresu 2003 - 2006:

▪ średni błąd predykcji (ME),

▪ średni błąd absolutny (MAE),

▪ średni absolutny błąd procentowy (MAPE),

▪ pierwiastek błędu średniokwadratowego (RMSE),

▪ współczynnik Theila.

Zadanie 7

Na podstawie danych przykładowych Gretla (Ramanathan: data2_3 Unemployment, Inflation, Wages) zbudować model na próbie zawężonej do roku 1993

Inlf _t= a₀ + a₁wggr_t + a₂unemp_t

Dokonać prognozy punktowej i przedziałowej na lata 1994 - 1995

Zmierzyć

▪ średni błąd predykcji (ME),

▪ średni błąd absolutny (MAE),

▪ średni absolutny błąd procentowy (MAPE),

▪ pierwiastek błędu średniokwadratowego (RMSE),

▪ współczynnik Theila.

Zweryfikuj hipotezę o stabilności parametrów modelu za pomocą testu Chowa

Zadanie 8

Oszacowano model postaci

Y_t =a + bX_1t − cX_2t t=1, ..., 40

Aby sprawdzić stabilność parametrów modelu, oszacowano dodatkowy model o tej samej postaci, ale na próbie zawężonej do grupy obserwacji w okresie t=1,... 20

Następnie oszacowano model tej samej postaci na próbie obserwacji z okresu t=21, ..., 40

Suma kwadratów reszt modelu oszacowanego na pełnej próbie wyniosła 230. Suma kwadratów reszt modelu szacowanego dla okresu t=1,...,20 wyniosła 125, a dla drugiego modelu 76. Czy wyjściowy model ma stabilne parametry?

Zadanie 9

Na podstawie danych o liczbie pasażerów linii lotniczych [pasazerowie linii lotniczych.xls]

Dokonaj prognozy liczby pasażerów w styczniu 1961 metodą średniej ruchomej (MA).

---