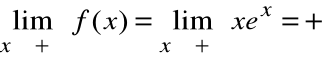2. Wklęsłość i wypukłość wykresu funkcji

Definicje 1

Funkcja f(x) jest wypukła (odp. wklęsła) na przedziale (a,b), jeśli odcinek łączący dwa dowolne punkty wykresu tej funkcji leży nad tym wykresem (odp. pod wykresem) z wyjątkiem końców odcinka.

Definicje 2

Funkcja f(x) jest wypukła (odp. wklęsła) w punkcie x₀, jeśli istnieje takie sąsiedztwo S=S(x₀, δ), że dla ∀(x ∈S)

punkty P(x, f(x)) wykresu leżą powyżej (odp. poniżej) stycznej poprowadzonej do wykresu w punkcie o odciętej x₀.

1. funkcja jest wklęsła

2. funkcja jest wypukła

Definicje 3

Funkcja f(x) jest wypukła (odp. wklęsła) na przedziale

(a,b), jeśli jest wypukła (odp. wklęsła) w każdym punkcie x ∈ (a,b).

1. funkcja jest wklęsła

2. funkcja jest wypukła

Warunek wystarczający wypukłości i wklęskości:

Jeśli

• f ′′ (x) > 0 dla ∀x ∈(a,b), to f(x) jest wypukła na tym przedziale;

• f ′′ (x) < 0 dla ∀x ∈(a,b), to f(x) jest wklęsła na tym przedziale.

Przykład 7.

Wyznaczyć przedziały wypukłości i wklęsłości funkcji:

f(x) = x⁴ - 6x²

1. D_f =R

2. f ′(x) = 4x³ - 12x

3. f ′′(x) = 12x² -12 = 12(x² - 1) = 12 (x-1)(x+1)

f ′′(x) > 0 dla x ∈ (- ∝, -1) ∪ (1, ∝)

4. f ′′(x) < 0 dla x ∈ (-1, 1)

X	(- ∝, -1)	(-1, 1)	(1, ∝)
f ′′(x)	+	-	+
f(x)	∪	∩	∪

Odp. Funkcja jest wypukła dla x ∈ (- ∝, -1) ∪ (1, ∝)

i jest wklęsła dla x ∈ (-1, 1).

Przykład 8.

Wyznaczyć przedziały wypukłości i wklęsłości funkcji:

f(x) = x lnx

1. D_f =R⁺ = {x ∈R : x>0}

2. f ′(x) = lnx +x ⋅1/x= 1 + lnx

3. D_{f ′} =R⁺ = {x ∈R : x>0}

4. f ′′(x) = 1/x

5. f ′′(x) > 0 dla ∀x (x ∈ D_f )

Odp. Funkcja jest wypukła dla ∀x (x ∈ D_f ).

3. Punkty przegięcia wykresu funkcji

Definicje

Punkt P(x₀, f(x₀)) nazywamy punktem przegięcia krzywej o równaniu y=f(x), jeżeli funkcja f(x) jest ciągła w punkcie x₀ oraz jest wklęsła w pewnym lewostronnym sąsiedztwie punktu x₀ i wypukła w pewnym prawostronnym jego sąsiedztwie albo na odwrót.

Warunek konieczny istnienia punktu przegięcia krzywej o równaniu y=f(x), jest

f ′′(x₀) =0

Warunek wystarczający istnienia punktu przegięcia

krzywej o równaniu y=f(x):

Punkt P(x₀, f(x₀)) jest punktem przegięcia krzywej o równaniu y=f(x), gdy

f ′′(x₀) =0

oraz druga pochodna funkcji f(x) zmienia znak przy przejściu przez x₀

Przykład 9.

Wyznaczyć punkty przegięcia funkcji

f(x) = x⁴e^-x

f ′(x) = 4x³e^-x -x⁴e^-x = (4x³ -x⁴ )e^-x

f ′′ (x) = (12x²-4x³)e^-x - (4x³ -x⁴ )e^-x = (x⁴- 8x³+ 12x²)e^-x = x²(x² - 8x + 12)e^-x

f ′′ (x) = 0 dla x=0, x=2, x=6.

f ′′ (x) < 0 dla (x² - 8x + 12) < 0 ⇒ x ∈ (2,6)

f ′′ (x) > 0 dla (x² - 8x + 12) > 0 ⇒

x ∈ (- ∝, 2) ∪ (6, ∝), x ≠0

x	(- ∝, 0)	0	(0, 2)	2	(2,6)	6	(6, ∝)
f ′′ (x)	+	0	+	0	-	0	+
f (x)	∪	0	∪	p.p.	∩	p.p.	∪

f(2)= 16e^-2, f(6) = 6⁴e^-6.

Odp. Punkty P₁(2, 16e^-2) oraz P₂(6, 6⁴e^-6 ) są punktami przegięcia funkcji f(x).

2. Warunek wystarczający istnienia punktu przegięcia

krzywej o równaniu y=f(x):

f(x) ma w pewnym sąsiedztwie punktu x₀ pochodne do rzędu n (n ≥ 3) włącznie;

• f⁽ⁿ⁾(x) jest ciągła w punkcie x₀;

• f ′′ (x₀) = f ′′′ (x₀) = … = f ^(n-1)(x₀)= 0;

• f⁽ⁿ⁾(x₀) ≠ 0;

• n jest liczbą nieparzystą,

to punkt P(x₀, f(x₀)) jest punktem przegięcia krzywej o równaniu y=f(x).

Przykład 10.

Wyznaczyć punkty przegięcia funkcji

f(x) = x⁵ - x + 3

f ′(x) = 5x⁴ - 1

f ′′ (x) = 20x³

f ′′′ (x) = 60x²

f⁽⁴⁾(x) = 120x

f⁽⁵⁾(x) = 120

Dla x=0

f ′(x) = f ′′ (x) = f ′′′ (x) = f⁽⁴⁾(x) =0

oraz

f⁽⁵⁾(x) = 120 ≠ 0

n=5 - liczba nieparzysta ⇒ punkt P(0,3) jest punktem przygięcia wykresu funkcji f(x).

4. Asymptoty wykresu funkcji

Asymptotą ukośną jest prosta o równaniu

y = ax+b

1)
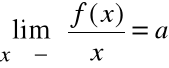
oraz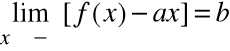

dla asymptoty ukośnej (lub poziomej, gdy a=0) lewostronną

2)
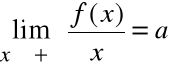
oraz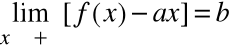

dla asymptoty ukośnej (lub poziomej, gdy a=0) prawostronną

Przykład 11.

Wyznaczyć asymptoty funkcji

f(x) =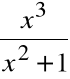

1)

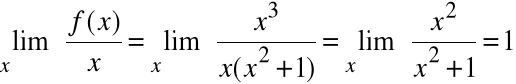
a=1

2)

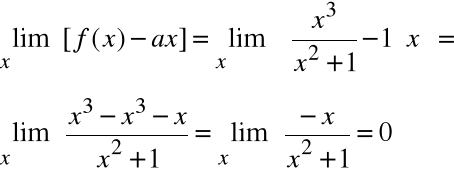
b=0

Zatem a=1, b=0. Prosta y=x jest asymptotą ukośną obustronną.

Definicje

Prostą o równaniu x=a nazywamy asymptotą pionową lewostronną wykresu funkcji f(x), gdy:

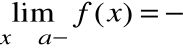
lub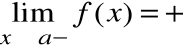

Definicje

Prostą o równaniu x=a nazywamy asymptotą pionową prawostronną wykresu funkcji f(x), gdy:

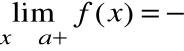
lub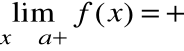

Przykład

f(x) = 2^1/x

y = 1 - asymptota pozioma obustronna

x = 0 - asymptota pionowa prawostronna

Przykład

x=π/2+πk ( k∈Z) - asymptoty pionowe obustronne

Przykład

x = x₀ - asymptota pionowa obustronna

Przykład 12.

Wyznaczyć asymptoty funkcji

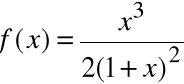
D_f = R \ {-1}

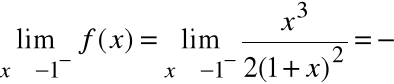
oraz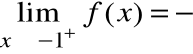

Zatem prosta x=-1 jest asymptotą pionową obustronną funkcji f(x).

5. Ogólny schemat badania przebiegu funkcji

I. Analiza funkcji.

• Dziedzina funkcji.

• Szczególne własności funkcji: parzystość, nieparzystość, okresowość itp.

• Punkty przycięcia wykresu funkcji z osiami układu współrzędnych.

• Ustalenie znaku funkcji.

• Granice funkcji na końcach przedziałów określoności.

• Punkty nieciągłości funkcji.

• Asymptoty funkcji.

II. Analiza pierwszej pochodnej.

• Obliczamy pierwszą pochodną.

• Dziedzina pierwszej pochodnej i jej punkty nieciągłości.

• Przedziały monotoniczności.

• Ekstrema lokalne funkcji.

III. Analiza drugiej pochodnej.

• Obliczamy drugą pochodną.

• Dziedzina drugiej pochodnej i jej punkty nieciągłości.

• Przedziały wklęsłości i wypukłości funkcji.

• Punkty przegięcia wykresu funkcji.

IV. Ostateczny szkic wykresu funkcji.

Przykład 13.

f(x) = xe^x

1. Df=R - funkcja jest ciąłga

2. f(-x) = -xe^-x ≠ f(x) - funkcja nie jest parzystą

3. f(-x) = -xe^-x ≠ - f(x) = -xe^x - funkcja nie jest nieparzystą

4. 
   

5. 
   

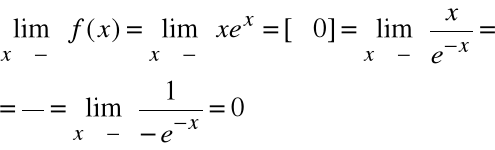
6. f(x)=0 ⇒ xe^x = 0 ⇒ x=0 ⇒ (0,0) - punkt przecięcia funkcji z osiami układu współrzędnych.

7. Ponieważ f(x) jest ciągła, nie posiada asymptot pionowych.

8. Ponieważ

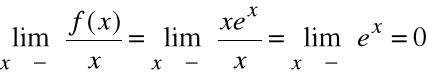
a=0

,

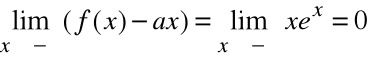
b=0

y=0 jest asymptotą poziomą lewostronną.

9. Ponieważ

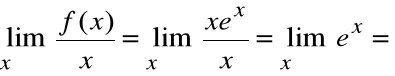
funkcja nie posiada asymptoty ukośną.

10. Obliczamy pierwszą pochodną:

f ′(x) = e^x + xe^x = (1+x)e^x.

Ponieważ e^x > 0 dla ∀x,

a) f ′(x) = 0 ⇔ 1 +x=0 ⇔ x = -1;

b) f ′(x) > 0 ⇔ 1+x >0 ⇔ x ∈(-1, ∝)

c) f ′(x) < 0 ⇔ 1+x <0 ⇔ x ∈(- ∝, -1)

funkcja rośnie dla x ∈(-1, ∝)

funkcja maleje dla x ∈(- ∝, -1)

x=-1 - punkt minimum lokalnego

f_min = f(-1) = -e^-1.

11. Obliczamy drugą pochodną:

f ′′ (x) = e^x + (1+x)e^x = (2+x)e^x.

a) f ′′ (x) = 0 ⇔ 2 +x=0 ⇔ x = -2;

b) f ′′ (x) > 0 ⇔ 2+x >0 ⇔ x ∈(-2, ∝)

c) f ′′ (x) < 0 ⇔ 2+x <0 ⇔ x ∈(- ∝, -2)

funkcja f(x) jest wypukła dla x ∈(-2, ∝)

funkcja f(x) jest wklęsła dla x ∈(- ∝, -2)

x=-2 - jest punktem przegięcia

---