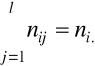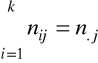DWUWYMIAROWY ROZKŁAD EMPIRYCZNY
Def. Empiryczny dwuwymiarowy rozkład cechy (X,Y) lub inaczej - empiryczny łączny rozkład cech X, Y określają liczebności nij (i=1,...,k; j=1,...,l) odpowiadające parom wartości (xi, yj).
![]()
Liczebności te muszą spełniać warunek:
![]()
gdzie n jest ogólną liczebnością zbiorowości.
Def. Rozkłady każdej z cech, traktowanych oddzielnie, określa się mianem rozkładów brzegowych (bezwarunkowych).
Def. Rozkład brzegowy (bezwarunkowy) cechy X wyznaczają liczebności ni. określone jako:
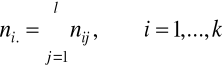
Liczebności ni. wskazują na to, ile jednostek zbiorowości przyjmuje wyróżnione wartości cechy X.
Def. Rozkład brzegowy (bezwarunkowy) cechy Y wyznaczają liczebności n.j, określone jako:
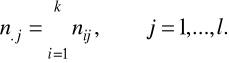
Dla liczebności nij, ni. oraz n.j(i=1,...,k; j=1,...,l) zachodzi:
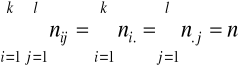
TABLICA KORELACYJNA CECH X I Y
xi |
y1 y2 . . . yl |
|
x1 x2 . . . xk |
n11 n12 . . . n1l n21 n22 . . . n2l . . . . . . . . . nk1 nk2 . . . nkl |
n1. n2. . . . nk. |
|
n.1 n.2 . . . n.l
|
n |
PARAMETRY DWUWYMIAROWEGO ROZKŁADU EMPIRYCZNEGO
Rozkłady brzegowe:
cechy X:
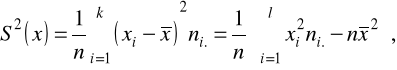
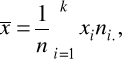
![]()
![]()
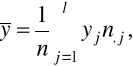
cechy Y:
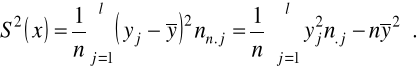
Rozkłady warunkowe:
cechy X:
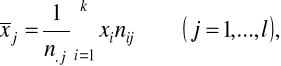
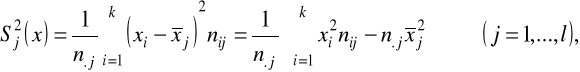
cechy Y:
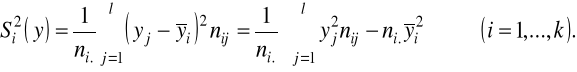
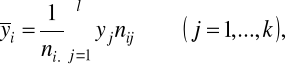
KOWARIANCJA DWUWYMIAROWEGO ROZKŁADU EMPIRYCZNEGO
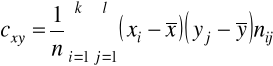
lub
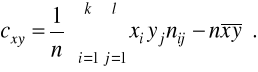
W przypadku korzystania z danych indywidualnych (xi, yi) (i=1,2,...,n) powyższe wzory można zapisać w następującej postaci:
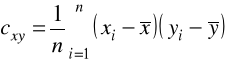
oraz
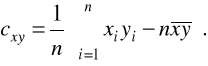
WSPÓŁCZYNNIK ZBIEŻNOŚCI V CRAMERA
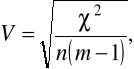
gdzie: m = min (k, l)
Własności:
jest symetryczny, tzn.:
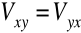
,
przyjmuje wartości z przedziału <0;1>,
w przypadku stochastycznej niezależności dwóch cech
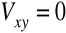
, natomiast, w przypadku związku funkcyjnego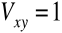
,
nie wskazuje kierunku korelacji dwóch cech,
może być stosowany zarówno w przypadku cech mierzalnych, jak i niemierzalnych.
WARUNKI ZALEŻNOŚCI STOCHASTYCZNEJ I KORELACYJNEJ
Def. Zmienne są stochastycznie zależne gdy wartość jednej zmiennej wpływa na rozkład prawdopodobieństwa drugiej zmiennej.
Warunki niezależności stochastycznej:
rozkłady warunkowe zmiennej losowej Y są identyczne (rozkłady warunkowe zmiennej Y mają jednakowe średnie i wariancje)
→ równość warunkowych średnich
![]()
→ równość warunkowych wariancji
![]()
Def. Zmienne są korelacyjne zależne gdy określonym wartościom jednej zmiennej przyporządkowane są średnie wartości drugiej zmiennej
Warunki niezależności korelacyjnej:
średnie warunkowe zmiennej losowej Y są identyczne (rozkłady warunkowe różnią się między sobą)
→ równość średnich warunkowych
![]()
WSKAŹNIKI (STOSUNKI KORELACYJNE)
Równość wariancyjna
![]()
![]()
miara ogólnego zróżnicowania cechy y
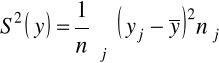
![]()
miara przeciętnego zróżnicowania cechy y wewnątrz rozkładów warunkowych
![]()
miara przeciętnego zróżnicowania cechy y między rozkładami warunkowymi
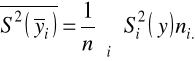
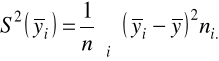
WSKAŹNIKI (STOSUNKI) KORELACYJNE
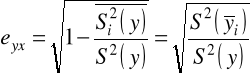
Własności:
wskaźnik korelacyjny nie jest symetryczny, tzn.
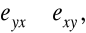
poza sytuacją niezależności cech lub związku funkcyjnego,
przyjmuje wartości <0;1>,
nie wykazuje kierunku korelacji dwóch cech,
w przypadku stochastycznej niezależności dwóch cech
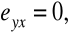
natomiast w przypadku związku funkcyjnego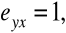
przynajmniej cecha zależna musi być mierzalna,
może być stosowany zarówno w przypadku związków korelacyjnych liniowych jak i nieliniowych.
WSPÓŁCZYNNIK KORELACJI LINIOWEJ
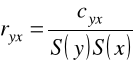
gdzie:
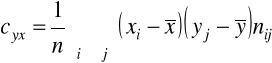
Własności:
jest symetryczny, tzn.
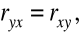
przyjmuje wartości z przedziału <-1; 1>,
charakteryzuje zarówno kierunek jak i siłę zależności dwóch cech,
ma zastosowanie wyłącznie gdy związek dwóch cech ma charakter liniowy,
może być wyznaczany wyłącznie w przypadku cech mierzalnych.
WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI KORELACYJNEJ W POPULACJI GENERALNEJ ZMIENNEJ
LOSOWEJ X OD ZMIENNEJ LOSOWEJ Y
1. Stawiamy hipotezę o liniowej niezależności korelacyjnej zmiennej losowej X od zmiennej losowej Y:
![]()
![]()
wobec hipotezy alternatywnej:
![]()
2. Jeżeli ![]()
jest prawdziwa, to statystyka o postaci:
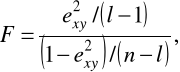
gdzie:
n - liczebność próby,
s - liczba wariantów zmiennej niezależnej Y w próbie,
exy - stosunek korelacyjny z próby,
ma rozkład F-Snedecora o liczbie stopni swobody ![]()
oraz ![]()
, a przy tym ta statystyka nie powinna przyjmować zbyt dużych wartości.
3. Przy danym poziomie istotności ustalamy wartość krytyczną ![]()
, której nie powinna przekraczać statystyka F, określając ją w taki sposób w rozkładzie F-Snedecora, aby zachodziła relacja:
![]()
4. Wartości zmiennej F spełniające nierówność ![]()
są obszarem krytycznym testu, tzn.:
![]()
5. Jeżeli z próby uzyskamy taką wartość statystyki F, że:
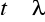
to hipotezę zerową odrzucamy na rzecz hipotezy alternatywnej,
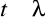
to stwierdzamy, że nie ma podstaw do odrzucenia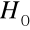
.
TEST DOTYCZĄCY WARTOŚCI WSPÓŁCZYNNIKA
KORELACJI
1. Stawiamy hipotezę, że współczynnik korelacji ![]()
w populacji generalnej jest równy zeru:
![]()
wobec hipotezy alternatywnej:
![]()
2. Jeżeli ![]()
jest prawdziwa, to statystyka o postaci:
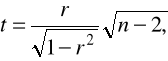
gdzie r jest współczynnikiem korelacji z próby, ma rozkład t-Studenta o s=n-2 stopniach swobody.
3. Przy danym poziomie istotności ustalamy wartość krytyczną ![]()
, której nie powinna przekraczać bezwzględna wartość statystyki t, określając ją w taki sposób w rozkładzie t-Studenta, aby zachodziła relacja:
![]()
4. Wartości zmiennej t spełniającej nierówność ![]()
są obszarem krytycznym testu, tzn.:
![]()
5. Jeżeli próby uzyskamy taką wartość statystyki t, że:
![]()
to hipotezę zerową odrzucamy na rzecz hipotezy alternatywnej,
![]()
to stwierdzamy, że nie ma podstaw do odrzucenia ![]()
.
MIARA KRZYWOLINIOWOŚCI ZWIĄZKU CECH
![]()
![]()
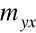
oraz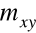
przyjmują wartości z przedziału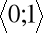
WSPÓŁCZYNNIK KORELACJI RANG
uszeregowanie badanych jednostek według kryterium porządkującego, niezależnie ze względu na badane cechy
nadanie rang wszystkim badanym jednostkom, tzn. numerów miejsc zajmowanych przez badane jednostki w ciągu uporządkowanych ze względu na badane cechy
obliczenie różnic pomiędzy rangami przyporządkowanymi poszczególnym badanym jednostkom w obu ciągach
obliczenie współczynnika korelacji rang:
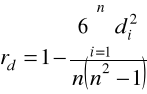
,
gdzie:
ai, bi - rangi nadane i-tej badanej jednostce w poszczególnych, uporządkowanych ciągach:
di = ai - bi
Własności:
umożliwia ocenę zarówno siły jak i kierunku zależności pomiędzy cechami niemierzalnymi
przyjmuje wartości z przedziału <-1,1>
jest miarą symetryczną
![]()
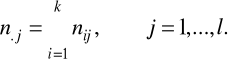
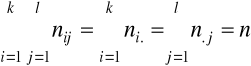
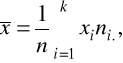
![]()
![]()
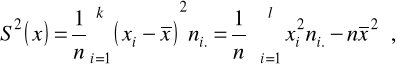
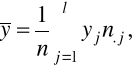
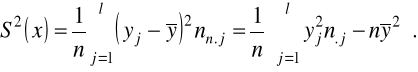
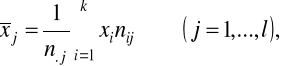
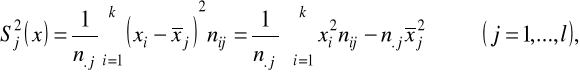
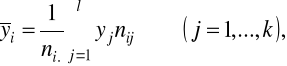
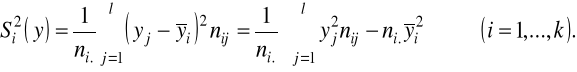
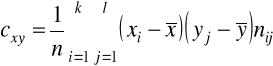
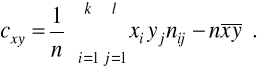
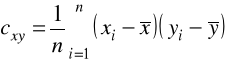
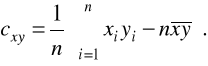
Wyszukiwarka
Podobne podstrony:
Definicja i podzia skazy krwotocznej
Ewolucja marketingu era produkcyjna, sprzedazowa, marketingowa Rynek definicja
BAD WYKŁAD SIECI 2
INTER 1 DEFINICJA
DEFINICJA STRESU
Definicje położnicze
wyklad3 tech bad
1 1 bezpiecz definicjeid 8843 ppt
2 Podstawowe definicje (2)id 19609 ppt
2 definicje i sprawozdawczośćid 19489 ppt
BM 4 Bad motywacyjne FGI IDI
Definicja zakażenia szpitalnego
wyklad 29 i 30 tech bad
2 bezp narod pojęcia definicje
Lekarski farmakologia kliniczna,definicja1
więcej podobnych podstron