ZAD3. Na jednej lince wiszą dwa odważniki, 10 kG i 5 kG umocowane na niej w różnych punktach przy czym większy z nich wisi na niżej od mniejszego. Jaka jest siła w lince powyżej lżejszego odważnika a jaka poniżej niego.

Rozwiązanie:

Prowadzimy myślowy przekrój I, wyodrębniający ciężar P =10 kG. Oznaczamy siłę działającą w lince między punktami A i B jako S1. Równanie równowagi: P1-S1=0 stad S1=10kG. Po wyznaczeniu S1 prowadzimy przekrój myślowy II, obejmujący ciężar P2 i przecinający linkę w 2 miejscach: miedzy A i B oraz nad B. Siłę w lince nad p. B oznaczamy S2. Siłami zewnętrznymi działającymi na układ SA S1, S2, P2. Rów. Równowagi: P2+S1-S2=0 => S2=15kG

ZAD5. Holownik parowy ciągnie 3 barki o różnych wymiarach, połączone jedna za drugą . Ciąg śruby holownika wynosi w danej chwili 1800 kG. Opór stawiany parowcowi przez wodę wynosi 600 kG. Opór wody działający na pierwszą barkę 600 kG, na drugą 400 kG, a na trzecią 200 kG. Użyta przy tym lina może być bezpiecznie obciążona siłą 200 kG.

Iloma linami należy połączyć parowiec z pierwszą barką, pierszą barkę z drugą oraz drugą z trzecią. Jeśli ruch jest prostoliniowy i jednostajny.

Rozwiązanie:

Siła w linach łączących ostatnią barkę z druga wynosi 200kG - wystarcza jedna lina, między druga a pierwsza 200+400=600kG 600/200-> 3 liny, między holownikiem a pierwszą 200+400+600=1200kG -> 6lin

ZAD7.Na dnie szybu znajduję się człowiek o ciężarze 64 kG i za pośrednictwem liny przerzuconej przez nieruchomy krążek, utrzymuje ciężar 48 kG

(a)jaką siłę wywiera człowiek na dno szybu

(b)jaki największy ciężar może on utrzymać za pomocą liny.

Rozwiązanie:

(a) Ciężar człowieka Q=64kG; siła w linie S=48kG. Nacisk stóp człowieka na podłogę N' jest równy co do wartości sile N, jaką podłoga wywiera na stopy człowieka: Q-N-S=0

N=Q-S=16kG. (b) dla N=0 (człowiek wisi na linie): Q=S.

ZAD18. Na rysunkach a,b, i c podobnie jak w zadania poprzednim pokazano schematycznie układy prętów o połączonych przegubowo ze sobą z sufitem i ze ścianą. Na sworzniach przegubów B , F , K zawieszono ciężary Q=1000 kG. Obliczyć siły w prętach.

(a)

(b)

(c)

Rozwiązanie:

Wykreślając trójkąty sił należy zaczynać od siły Q, a następnie kreślić siły w prętach (czyli na wykresie równoległe do prętów) kolejno, jak je napotkamy obiegając rozważany węzeł w obranym kierunku, np. zgodnie ze wskazówkami zegara. Rozpoczynając od siły danej. (a) S1=S2=+Qsin45=+707kG (b) S1=+Qtg30=+577kG, S2=-Q/cos30=-1155kG (c) S1=-Qtg30=-577kG, S2=+Q/cos30=+1155kG

ZAD19.Latarnia uliczna zawieszona jest w punkcie B w środku linki ABC przyczepionej do haków A i C znajdujących się na jednym poziomie. Znaleźć siły T₁ i T₂, rozciągające część linki AB i BC, jeżeli ciężar latarni wynosi 15 kG, długość całej linki 20m, odległość zaś BD punktu zawieszenia B od poziomej AC wynosi 0,1m. Ciężar linki pominąć.

Rozwiązanie:

Wykreślamy trójkąt sił. Ciężar latarni Q=15kG; ze względu na symetrię jest T1=T2. Połowa trójkąta sił oznaczona literami abd jest podobna do trójkąta ABD na rysunku do zadania.

ZAD20.Latarnia uliczna o ciężarze 30 kG zawieszona jest na pionowym słupie za pomocą poziomej poprzeczki AC=1,2m oraz ukośnego pręta BC=1,5m . Obliczyć siły S₁ i S₂ w prętach AC i BC, jeżeli połączenia w punktach A B C są przegubowe.

Rozwiązanie:

Trójkąt sił jest podobny do trójkąta ABC na rysunku do zadania. Stąd

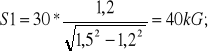
ZAD21.Lampa elektryczna o ciężarze 2 kG zawieszona jest sufitu na sznurze AB i przyciągnięta do ściany linką BC. Wyznaczyć siły: T_A w sznurze AB i T_c w lince BC. Jeżeli wiadomo, że kąt
Ciężar sznura i linki pominąć.

Rozwiązanie:

Ta/sin45=Q/sin105,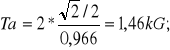
Tc/sin30=Q/sin105, Tc=1,035kG

ZAD22.Dźwig słupowy składa się z ramienia AB przyczepionego do słupa przegubem A i łańcuchem CB. Na końcu B ramienia zawieszony jest ciężar P=200kG. Kąt BAC=
Kąt ACB=
Wyznaczyć siłę T w łańcuchu CB i siłę Q w ramieniu AB.

Rozwiązanie:

Z trójkąta sił:

T/sin15=P/sin30, T=200*(0,2588/0,5)=103,5kG; Q=-P*sin135/sin30=-282,8kG

ZAD25.Ciało o ciężarze 25kG utrzymywane jest w równowadze przez dwie linki przerzucone przez krążki i obciążone odważnikami. Jeden z tych odważników waży 20kG, Sinus kąta utworzonego przez odpowiednią linkę z pionem wynosi 0,6. Pomijając tarcie na krążkach wyznaczyć ciężar p drugiego odważnika oraz kąt

utworzony przez drugą linkę z pionem, nie uwzględniać ciężaru linki .

Rozwiązanie:

Dane: G=25kG, q=20kG, sinB=0,6. Równania sum rzutów sił działających na węzeł C na kierunki poziomy i pionowy:

qsinB-psinA=0 => p=qsinB/sina; qcosB+pcosA-G=0 => qcosB+qsinBctgA-G=0;

=> A=53^o10';

ZAD26.Do linki AB której jeden koniec umocowany jest w punkcie A przywiązano w punkcie B ciężar P i linkę BCD przerzucono przez krążek. Do końca D linki przywiązano ciężar Q=10Kg.Obliczyć siłę T w lince AB i ciężar P jeżeli w położeniu równowagi kąty utworzone przez linki z pionem BE wynoszą
Tarcie na krążku pominąć.`

Rozwiązanie:

Z trójkąta sił:

,
;
,

ZAD29. Przy pionowej gładkiej ścianie AB zawieszono jednorodną kulę O na lince AC.

Linka tworzy ze ścianą kąt
Ciężar kuli wynosi P. Obliczyć siłę T w lince i oddziaływanie Q kuli na ścianę.

Rozwiązanie:

Na kule działają 3 siły: ciężar P, siła w sznurze T oraz oddziaływanie ściany na kulę Q'. Z warunków równowagi układu 3 sił wynika, że musza one przecinać się w jednym punkcie. Siły P i Q' przechodzą przez środek kuli O, a więc i siła T musi przez ten punkt przechodzić. Kula zawieszona i oparta o ścianę przyjmie taką położenie żeby jej środek ciężkości leżał na linii przedłużenia sznurka. (jeśli nie występuje tarcie). Z trójkąta sił: Q'=PtgA, T=P/cosA. Nacisk Q kuli na ścianę będzie miał te sama wartość i przeciwny zwrot.

ZAD32.Jednorodna kula o ciężarze 10 Kg, utrzymywana jest w położeniu równowagi przez dwie linki AB i CD rozpięte w jednej płaszczyźnie pionowej i tworzące kąt
Linka AB tworzy z poziomem kąt
. Obliczyć siłę w linkach.

Rozwiązanie:

Z trójkąta sił.
,
;
,

ZAD39.Belka AB utrzymywana jest w położeniu poziomym przez pręt CD; Połączenia w punktach A, C, D są przegubowe . Wyznaczyć reakcję podpór A i D jeżeli na koniec belki działa pionowa siła F=5 T. Wymiary pokazane są na rysunku. Ciężar własny belki pominąć.

Rozwiązanie:

Na przecięciu linii działania siły F i osi pręta CD znajdujemy punkt E, przez który musi przechodzić linia działania trzeciej siły działającej na belkę, tj. Ra. Mając kierunki sil wykreślamy trójkąt sił (rys). Wartości sił obliczamy z wykresu, w skali obranej dla siły F, albo z twierdzenia sinusów. Obliczywszy uprzednio kąty trójkąta sil, po czym z wykresu znajdujemy tga=1/3

ZAD40. Koniec A belki umocowany jest przegubowo, koniec B zaś wsparty na wałkach. W środku belki zaczepiona jest siła P=2 t, działająca pod kątem
do jej osi. Biorąc wymiary z rysunku, wyznaczyć w przypadkach (a) i (b) reakcję podpór A i B, Ciężar własny belki pominąć.

Rozwiązanie:

Rozwiązania wykreślne identyczne jak w zad. 39. W przypadku (a) jest tga=1/2 w przypadku (b) zaś tga=1/3.

ZAD50.Do trójprzegubowego łyku ACB pokazanego na rysunku wyznaczyć reakcję podpór A i B powstające pod działaniem poziomej siły P.

Rozwiązanie:

Ponieważ na łuk BC działają tylko 2 siły (oddziaływanie w przegubach B i C) więc siły te musza leżeć na prostej BC. Na łuk AC 3 siły: siła dana P; oddziaływanie łuku BC oraz reakcje Ra. Linie działania pierwszych dwóch sił przecinają się w punkcie C, więc i linia działania 3 siły tez musi przechodzić przez C. Mając kierunki reakcji Ra i Rb wykreślamy trójkąt sił z którego znajdujemy Ra=Rb=

ZAD64. Wieża ciśnień składa się z walcowego zbiornika o wysokości 6m i średnicy 4 m, ustawionego na czterech symetrycznie rozstawionych pochyłych słupach. Dno zbiornika znajduję się na wysokości 17m nad fundamentem. Ciężar wieży 8T; przy obliczaniu siły wiatru bierzemy pod uwagę powierzchnię rzutu zbiornika na płaszczyznę prostopadłą do kierunku wiatru i przyjmujemy że parcie wiatru wynosi 125kG/m². Obliczyć niezbędną odległość AB między podstawami słupów.

Rozwiązanie:

W najniekorzystniejszym przypadku, gdy parcie wiatru jest największe (takie, jakie uwzględniamy w konstrukcji wiezy): P=4*6*125=3000kG=3T, a ciężar wieży najmniejszy (tj. zbiornik jest pusty i ciężar wiezy to tylko ciężar konstrukcji): Q=8T, wypadkowa tych dwóch sil, przechodząca przez srodek zbiornika, ma największy kąt odchylenia od pionu: tga=P/Q=3/8. Punkt B, w którym linia działania wypadkowej W przebija płaszczyznę podstawy wieży, jest najbliższym osi OC dopuszczalnym położeniem podpory wiezym, a więc CB=OCtga=7,5m. W tym przypadku podpora A, symetryczna do B będzie całkowicie odciążona, Ra=0, Rb=W. Gdyby CB<OCtga, to w rozpatrywanym przypadku podpora A byłaby odrywana od podstawy, czego się w zadaniu nie zakłada. Ten sam wynik otrzymamy, jeżeli wykorzystamy warunek, aby moment przewracający wieżę dookoła punktu B nie bbył większy niż moment siły ciężkości:
; stąd

ZAD77.Jednorodny pręt AB, o długości 1m i ciężarze 2 kG, zawieszony jest poziomo na dwóch równoległych linkach AC i BD. Na pręcie w punkcie E odległym o AE=1/4m od punktu A, Zawieszono ciężar P=12kG. Obliczyć siły w linkach , T_C I T_D

Rozwiązanie:

Ciężar pręta Q=2kG przyłozony jest w punkcie F na połowie długości pręta. Równanie momentów względem punktu A:

P*AE+Q*AF-Td*AB=0; stąd

Równanie momentów względem B:

Tc*AB-P*EB-Q*FB=0; stąd

ZAD78.Na poziomej belce leżącej na dwóch podporach odległych o 4 m położono dwa ciężary: jeden C=200kG, drugi D=100Kg, tak że reakcja podpory A jest dwa razy większa od reakcji podpory B. Ciężar własny belki pomijamy, odległość CD między ciężarami wynosi 1m. Jaka jest odległość x ciężaru C od podpory A?

Rozwiązanie:

Z danych wynika, że reakcja Ra=2Rb. Równanie sumy rzutów sił na kierunek pionowy: Ra-C-D+Rb=0; stąd 2Rb-200-100+Rb=0, Rb=100kG

Równania momentów względem punktu A:

Cx+D(x+1)-Rb*AB=0 stąd 200x+100(x+1)-100*4=0 -> x=1m

ZAD81.Jednorodna belka AB o długości 10m i ciężarze 200kG leży na dwóch podporach C i D. Podpora C odległa jest od końca A o 2m, podpora D od końca B o 3m. Koniec belki A podciągany jest pionowo ku górze przez ciężar Q=300kG, przywiązany do liny przerzuconej przez krążek. W odległości 3m od końca A zawieszony jest na belce ciężar P=800kG.Wyznaczyć reakcję podpór pomijając tarcie na krążku.

Rozwiązanie:

Ustawiamy równanie sumy momentów sił względem punktu C (aby z tego równania wyeliminować nieznaną reakcje
):

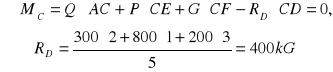
Równanie momentów względem punktu D:

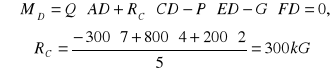
ZAD82.Poziomy pręt AB o ciężarze 100G może obracać się dookoła nieruchomego punktu A. Koniec B pręta jest podciągany ku górze przerzuconą przez krążek linką z uwiązanym na końcu ciężarem P=150G.W punkcie znajdującym się w odległości 20cm od końca B zawieszony jest ciężar Q =500G. Jaka jest długość x pręta AB, jeśli znajduje się on w równowadze?

Rozwiązanie:

Oznaczamy szukaną długość pręta AB = x cm.

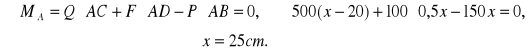
ZAD89.Na poziomą belkę wspornikową działa para sił o momencie M=6 Tm, a w punkcie C pionowa siła P=2 T. Rozpiętość belki AB=3,5m, długość wspornika BC=0,5m. Wyznaczyć reakcje podpór.

Rozwiązanie:

Ponieważ siła P oraz reakcja
podpory B mają kierunek pionowy, więc i reakcja podpory przegubowej nieruchomej A musi mieć kierunek pionowy.

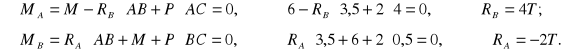
ZAD115.Jednorodna kula o ciężarze Q i promieniu a oraz ciężarek P wiszą na linkach zaczepionych w punkcie O, jak pokazano na rysunku. Odległość OM= b. Wyznaczyć kąt
, jaki tworzy w położeniu równowagi prosta OM z pionem .

Rozwiązanie:

Dane: promień kuli MB = a; odległość MO = b. Należy przyjąć, że między kulą i sznurkiem na odcinku BC nie występuje tarcie, gdyż tylko w tym przypadku nacisk N, jaki wywiera na kulę odcinek sznurka BC, przechodzi przez środek kuli i tylko wtedy kierunek OA przechodzi przez środek kuli M. Warunek równowagi układu: kula M, ciężar P i sznury, dla którego siłami zewnętrznymi są siły ciężkości kuli i ciężaru oraz reakcja w punkcie O:

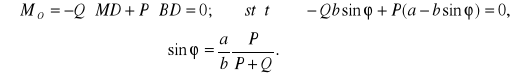
ZAD119.Jednorodna belka o ciężarze 60kG i długości 4m, opierająca się jednym końcem na gładkiej podłodze, a w pośrednim punkcie B- na słupie o wysokości 3m, tworzy z pionem kat
.Belka utrzymywana jest w takim położeniu przez Linke AC, przeciągnięta wzdłuż podłogi .Wyznaczyć siłę w lince T reakcję R_B I R_C. Tarcie pominąć.]

Rozwiązanie:

Oznaczenia widoczne z rysunku; 2l = 4m, h = 3m, Q = 60kG.

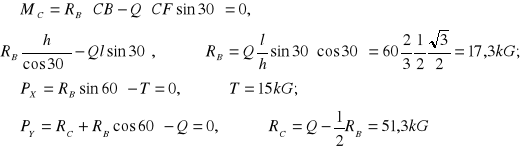
ZAD122.Jednorodny pręt AB o ciężarze 100kG opiera się jednym końcem na gładkiej poziomej podłodze, drugim zaś na gładkiej płaszczyźnie nachylonej pod kątem
do poziomu. Koniec B pręta podtrzymywany jest przez linkę przerzuconą przez krążek C i obciążoną ciężarem P. Część linki BC jest równoległa do pochyłej płaszczyzny. Pomijając tarcie na krążku wyznaczyć ciężar P i oddziaływania N_A i N_B na podłogę i pochyłą płaszczyznę.

Rozwiązanie:

Reakcje
podłoża na końce pręta AB są prostopadłe do podłoża. Ciężar pręta Q = 100kG. Przyjmijmy, że
, wypadkowa sił P i
, jest odchylona od pionu o kąt
. Obliczając sumę rzutów sił na kierunek poziomy znajdziemy:
a więc wypadkowa
ma kierunek pionowy, co również wynika z twierdzenia o układzie trzech sił. Ponieważ siły Q i
są pionowe, więc trzecia siła
musi być pionowa.

ZAD125 Do gładkiej ściany jest przystawiona jednorodna drabina AB, nachylona pod kątem
do poziomu. Ciężar drabiny wynosi 20kG. W punkcie D odległym od dolnego końca o 1/3długości drabiny stoi człowiek o ciężarze 60 kG. Znaleźć oddziaływanie drabiny na podporę A i na ścianę.

Rozwiązanie:

Ciężar człowieka
ciężar drabiny
.

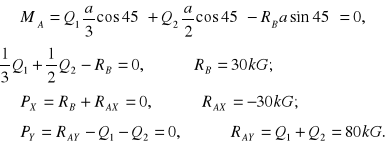
mom

ZAD137. Normalne oddziaływanie każdego z tylnych kół samochodu na nawierzchnię na drodze poziomej wynosi 500kG. Jakie będzie normalne oddziaływanie tych kół na drogę nachyloną do poziomu pod kątem
jeżeli wzniesienie środka ciężkości wynosi h=0,8, a rozstaw kół b=1,4m?

Rozwiązanie:

Obciążenie obu kół równa się

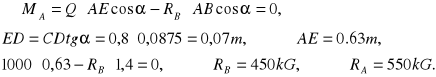
Składowe normalne nacisku kół na drogę:

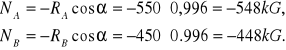
ZAD143 Most składa się z dwóch części złączonych przegubem A i przymocowanych do przyczółków przegubami B i C . Ciężar każdej części mostu wynosi 4T ich środki ciężkości leżą w punktach D i E. Na moście znajduje się ciężar P=2T. Wymiary pokazane są na rysunku. Obliczyć reakcje działająca na przegub A reakcje w punktarce B i C.

Rozwiązanie:

Dane: ciężar każdej części mostu Q = 4T; ciężar P = 2T. W przegubie A części mostu oddziałują na siebie wzajemnie siłami
równymi co do wartości i przeciwnie zwróconymi. Reakcję działającą na część II (prawą) mostu oznaczamy
z składowymi
, a reakcję działającą na część I mostu oznaczamy
a składowymi
W przegubach B i C działają na części mostu reakcje
ze składowymi
oraz
ze składowymi
Mamy zatem sześć niewiadomych:
Ponieważ most składa się z dwóch członów, możemy ustawić 2*3=6 równań równowagi, a więc zadanie jest statycznie wyznaczalne. Aby uzyskać najprostszy układ równań, napiszemy równania dla części II (na którą działa tylko jedna siła czynna Q) i dla całości (gdyż wtedy w drugim układzie trzech równań nie będą występowały składowe
jako siły wewnętrzne dla układu). Równania równowagi dla części II :

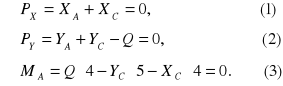
Równania równowagi dla całości:

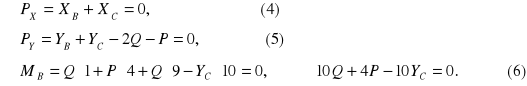
Rozwiązanie układu sześciu równań:

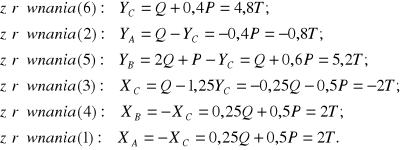
W przegubie A na część II działa reakcja o składowych
a na część I (lewą) reakcja o składowych

ZAD153. Dwa pręty AC i BD mające równe długości są połączone przegubowo w punkcie D oraz przymocowane do pionowej ściany w punktach A i B .Pręt AC położony jest poziomo, pręt BD tworzy z pionowa ścianą kąt
.Pręt AC jest obciążony w punkcie E pionowa siła
P₁=40Kg, a w punkcie C siła Q=100kG nachylona do poziomu pod katem
Pręt BD w punkcie F obciąża pionowa siła P₂=40kG.Wiedząc że AE= EC, BF= FD , wyznaczyć reakcje przegubów A i B.

Rozwiązanie:

Dane: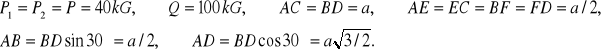

Równania równowagi dla całego układu:

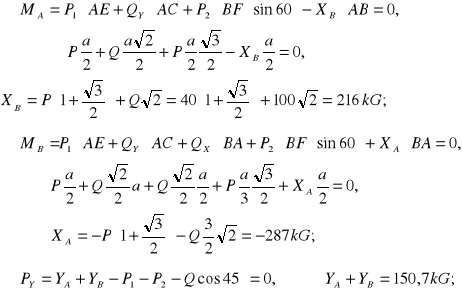
Dla belki BD:

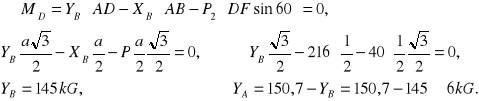
ZAD170 Trzy jednakowe rury o ciężarze P=120kG każda leża, jak pokazano na rysunku. Oblicz oddziaływanie dolnych rur na podłoże i na boczne gładkie ściany. Tarcie pominąć.

Rozwiązanie:

Równanie równowagi dla górnej rury:

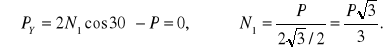
Nacisk na ścianę boczną:

Nacisk rur dolnych na podłoże:

Zwroty N i
podane na rysunku odnoszą się do reakcji ścian na rury.

ZAD171 Do wału przyłożono parę sił o momencie M=100kGm. Na wale zaklinowany jest bęben hamulcowy, którego promień r=25cm. Obliczyć jaką siłą Q należy dociskać do bębna klocki hamulcowe, aby unieruchomić wal , jeżeli współczynnik tarcia statycznego klocków po bębnie

Rozwiązanie:

Siły tarcia wynoszą
Zatrzymanie nastąpi gdy

ZAD176 Poziomy wysięgnik AB ma na końcu A tuleję o długości b=2cm, za pomocą której osadzony jest na pionowym wałku CD. W punkcie E w odległości a od osi wałka wisi na pręcie ciężar P. Pomijając ciężar pręta AB wyznaczyć odległość a tak aby pod działaniem ciężaru P pręt pozostawał w równowadze. Współczynnik tarcia między prętem a wałkiem wynosi

Rozwiązanie:

Przesunięcie a siły Względem osi wałka daje moment Pa, który musi być zrównoważony przez moment sił powstających w narożach F i G.

Równania równowagi wysięgnika:

A więc i siły tarcia
są jednakowe:
i dają wypadkową leżącą na osi wałka;

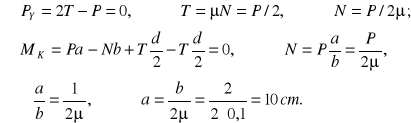
ZAD177. Do pionowej ściany przystawiona jest drabina AB oparta dolnym końcem o poziomą podłogę. Współczynnik tarcia drabiny o ścianę wynosi
_1, a o podłogę
_{2 .} Ciężar drabiny wraz ze znajdującym się na nim człowiekiem wynosi P i przyłożone jest w punkcie C, który dzieli długośc drabiny w stosunku m:n . Wyznaczyć największy kąt
zawarty między ścianą a drabiną w położeniu równowagi oraz normalne składowe reakcji ściany N_A i podłogi N_B dla tej wartości kąta

Rozwiązanie:

Przy obsuwaniu się drabiny w dół (zwiększanie kąta
) siły tarcia
mają zwrot jak pokazano na rysunku. Przy całkowicie rozwiniętej w obu punktach sile tarcia mamy zależności:
Równania równowagi drabiny:

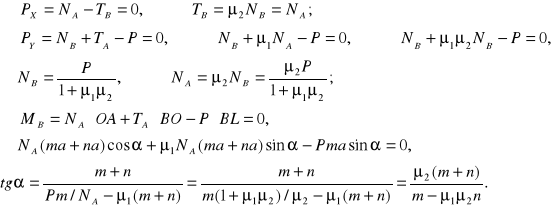
ZAD181. Jednorodna belka AB opiera się w punkcie A na chropowatej poziomej podłodze, koniec B zaś jest podtrzymywany przez linkę. Współczynnik tarcia belki o podłogę wynosi
,a kąt a utworzony przez belkę i podłogę wynosi
. Przy jakim kącie nachylenia linki do poziomu belka zacznie się poruszać?

Rozwiązanie:

Równania równowagi pręta:

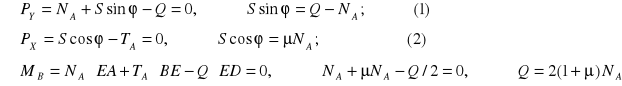
Dzieląc stronami (1) przez (2) otrzymujemy:

ZAD191 Wyznaczyć siłę P potrzebną do jednostajnego toczenia walca o średnicy 60cm i o ciężarze 300kG po poziomej płaszczyźnie, jeżeli współczynnik tarcia przy toczeniu wynosi
a kąt jaki siła tworzy z poziomem

Rozwiązanie:

Moment oporu przy toczeniu:
; moment obracający:
Warunek równowagi: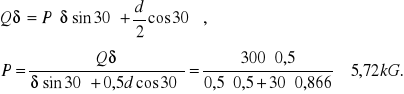

ZAD198. Wyznaczyć wykreślnie i sprawdzić analitycznie reakcje podpór i siły w prętach wiązania dachowego przedstawionego na rysunku z przyłożonymi doń siłami 3T, 2T i 1T.

Rozwiązanie:

Sprawdzamy warunek statycznej wyznaczalności i sztywności geometrycznej kratownicy: liczba prętów p = 9, liczba węzłów w = 6;

2w-3=2*6-3=9=p

Budujemy wielobok sznurowy; stąd wyznaczamy wartości reakcji i budujemy wykres Cremony, z którego odczytujemy wartości sił w prętach

ZAD203 Wyznaczyć wykreślnie i sprawdzić analitycznie reakcje podpór i siły w prętach kratownicy przedstawionej na rysunku.(Wskazówka: w tym i w następnych zadaniach oś Oz skierowana jest wzdłuż prostej poziomej w prawo, a oś Oy- pionowo do góry )

Rozwiązanie:

Reakcje wyznaczone z trójkąta sił, bez budowania wieloboku sznurowego, gdyż w tym zadaniu łatwo jest wykreślić wypadkową sił czynnych P₁ i P₂, która przecina w punkcie F, leżącym w granicach rysunku, znaną linię działania reakcji R_B. Prowadząc prostą FA, wyznaczamy kierunek reakcji R_A i z trójkąta sił odczytujemy wartości reakcji.

Sprawdzenie: p = 9, w = 6; 2w - 3 = 2*6 - 3 = 9 = p.

Dla wykresu Cremony budujemy wielobok sił, kreśląc siły w porządku, w jakim następują po sobie przy obieganiu kratownicy w kierunku zgodnym z wskazówek zegara. Z wykresu odczytujemy wartości sił w prętach.

ZAD204 Wyznaczyć reakcję podpór i siły w prętach kratownicy przedstawionej, razem z obciążeniami, na rysunku.

Rozwiązanie:

Sprawdzamy: p=9, ω=6; 2ω-3=2*6-3=9=p. Aby wyznaczyć reakcje metodą wykreślną, budujemy wielobok sznurowy zaczynając od punktu A. Do wykresu Cremony budujemy wielobok sił. Po wykonaniu wykresu Cremony odczytujemy wartości sił w prętach.

ZAD256 Robotnik podnosi ciężar Q=80kG za pomocą kołowrotu przedstawionego schematycznie na rysunku. Promień bębna R=5cm, długość ramienia korby AK=40cm, AC= CB =50cm. Wyznaczyć siłę P działającą na korbę i oddziaływanie osi kołowrotu na podpory A i B przy poziomym położeniu ramienia korby. Siłę P przyjąć jako pionową.

Rozwiązanie:

- reakcje działające na wał AB

, 80*5-P*40=0, P=10KG. Z_A=P=10kG, Z_B=0

, 80*50+X_B*100=0, X_B=-40kG

, X_A-40+80=0, X_A=-40kG,

N_Ax=40kG, N_Bx=40kG, N_Az= -10kG, N_Bz=0

ZAD257 Za pomocą kołowrotu, przedstawionego schematycznie na rysunku , podnoszony jest ciężar Q=100Kg. Promień bębna wynosi R=5cm, długość ramienia korby KD=40cm, DA=30cm, AC=40cm, CB=60cm.Lina schodzi z bębna po stycznej nachylonej do poziomu pod kątem
. Wyznaczyć siłę P działającą na korbę i reakcje podpór A i B, jeśli ramie korby jest w położeniu poziomym.

Rozwiązanie:

P=QR/KD=100*5/40=12,5kG

Z_B*100+100sin60°*40+12,5*30=0, Z_B=38,4kG

, Z_A+38,4+100sin60°-12,5=0, Z_A= - 35,7kG

, X_B*100+100cos60° *40=0, X_B= -20kG

, X_A -20+100cos60°=0, X_A= -30kG

ZAD265 Jednorodna rama prostokątna o ciężarze 20kG przymocowana do ściany za pomocą kulistego przegubu A i zawiasu B jest utrzymywana w położeniu poziomym linką CE zaczepioną do ramy w punkcie C i do gwoździa w punkcie E. Gwóźdź jest wbity do ściany na prostej pionowej przechodzącej przez A, przy czym
=
. Wyznaczyć siłę w lince i reakcje podpór.

Rozwiązanie:

, X_B=0,
, Z_B=0

Na półkę działają tylko trzy siły: Q,T,R_A. Siły te muszą przecinać się w punkcie F; stąd T=R_A

, 2Tsin30°=Q, T=R_A=Q=20kG;

Z_A=R_Asin30°=10kG; R_A(xy)=R_Acos30°;

X_A= R_A(xy)sin30°= R_Acos30°sin30°=8,66kG;

Y_A= R_A(xy)cos30°= R_Acos30°cos30°=15kG

ZAD270 Drzwi prostokątne o pionowej osi obrotu AB są uchylone o kąt CAD=
i utrzymywane w tym położeniu dwiema linkami, z których jedna CD, przerzucona jest przez blok i o9bciazona ciężarem P=32kG, druga EF, jest przywiązana do punktu F podłogi. Ciężar drzwi wynosi 64kG, szerokość AD=AC=180cm a wysokość AB=240cm. Pomijając tarcie bloku wyznaczyć sile T w lince EF oraz reakcje zawiasu walcowego w punkcie A i stopowego w punkcie B.

Rozwiązanie:

Z rysunku: AK
CD, AK=ACsin60°=AC
/4, BL=AC/2, BM=BLcos60°=AC/4,

LM=BLsin60°=AC
/4

, T=P=32kG

;

Y_A=-Psin30°-Q*AC/4AB=-28kG

;
; X_B=20,8kG

; -28+Y_B-32+32*1/2=0; Y_B=44kG

; Z_B=Q=64kG

ZAD286 Wyznaczyć położenia środka ciężkości C ramki AFBD składającej się z łuku ADB będącego ćwiartką okręgu koła o promieniu FD= R i półokręgu AFB zbudowanego na cięciwie AB jako na średnicy. Ciężar jednostki długości obu prętów tworzących ramkę jest jednakowy.

Rozwiązanie:

Odcięta środka ciężkości łuku AFT

FC₁=FE-EC₁=FE-FE*2/π=FE*(1-2/π); FE=R*
, więc FC₁= R*
* (1-2/π)

Długość łuku AFE oznaczmy l₁=FE*π =R π
. Dla łuku Abd o długosci l₂=R π/2 jest

. Odcięta środka ciężkości całej ramki

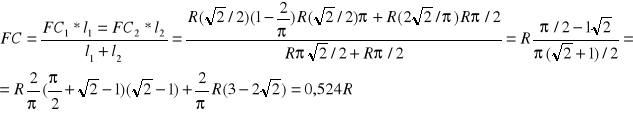
ZAD287 Wyznaczyć położenie środka ciężkości C powierzchni ograniczonej półokręgiem AOB o promieniu R i dwoma odcinkami równej długości AD i DB, jeśli OD= 3 R.

Rozwiązanie:

Półkole ABO: pole S₁=πR²/2; odcięta środka ciężkości OC₁=OE-EC₁=R-4/3*R/π=R(1-4/3π)

Trójkąt ABD: pole S₂=2R²; odcięta środka ciężkości OC₂=OE+EC₂=R+2R/3=5/3R

Dla całości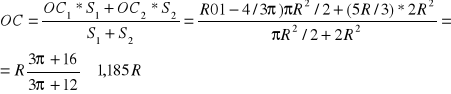

ZAD291 Znaleźć odległość środka ciężkości przekroju teownika ABCD od jego boku AC jeżeli wysokość środnika DB= h, szerokość półki AC=
, grubość półki wynosi d,a grubość środnika b.

Rozwiązanie:

Teownik dzielimy na dwa prostokąty pokazane na rysunku;

S₁=(h-d)b, y₁=(h+d)/2, S₂=ad, y₂=d/2;

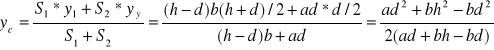
ZAD295 Przeprowadzić przez wierzchołek D jednorodnego prostokąta ABCD prostą DE tak, aby po odcięciu części wzdłuż tej prostej i zawieszeniu pozostałego trapezu za wierzchołek E , bok AD o długości a znalazł się w położeniu poziomym.

Rozwiązanie:

Aby bok AD pozostawał w położeniu poziomym przy zawieszeniu płytki w punkcie E, srodek ciężkości F obciętej płytki musi leżeć na prostopadłej opuszczonej z punktu E na bok AD, a więc X_F=EB=x

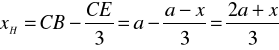
Pole trapezu ADEB

Pole trójkąta DCE

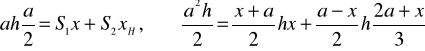
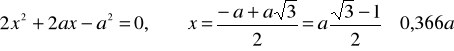
ZAD296 Dany jest kwadrat ABCD którego boki mają długość a. Znaleźć takie położenie punktu E, aby był on środkiem ciężkości powierzchni powstałej po wycięciu z kwadratu równoramiennego trójkąta AEB

Rozwiązanie:

Pole trójkąta ABE jest S₁=az/; rzędna środka ciężkości F tego trójkąta: z₁=HF=z/3; x=x₁=a/2. Pole figury AEBDC jest S₂=a²-az/2; dla całego kwadratu: S=a², z_śc= a/2. Zatem

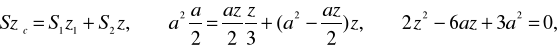
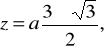
a ponieważ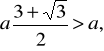
więc tylko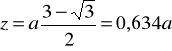

ZAD310 Ciało zawieszone na sprężystej linie drga zgodnie z równaniem:
, gdzie a wyrażone jest (¹) w cm, k w s^-1. Obliczyć amplitudę drgań i częstość kołową czyli pulsacje drgań ciała, jeżeli okres drgań wynosi 0,4s, a w chwili początkowej x_{0 =} -4cm. Narysować wykres współrzędnej x w zależności od czasu t.

Rozwiązanie:

Ponieważ wartość asin(kt+3π/2) zawarta jest w granicach ±a. więc amplituda x jest a. dla t=0 było xo=asin3π/2=-a=-4cm; a=4cm. Częstośc kołowa drgań, czyli pulsacja k=2π/T=2π/0,4=5π^-1

ZAD311 Z podanych równań ruchu punktu wyprowadzić równania toru.

(1)x=20t²+5, y=15t²+3

(2)x=4t-2t², y=3t-1,5t²

(3)x=5+3cos t, y=4sin t

(4)x = at², y = bt

(5)x=5 sin
, y=4 cos

(6)x= 5 cos t, y = 3-5sin t

(7)x= 3+4 cos t , y = 2 +5 sin t

(8)x= 3 cos

, y= 4 sin

Rozwiązanie:

Przypadek (1)

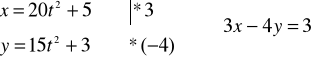
- prosta ;

niezależnie od wartości t jest x≥5, y≥3

Przypadek (2)

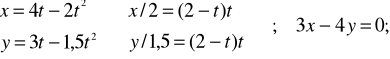
Ograniczenia: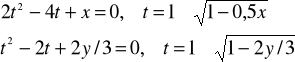

Aby t miało wartość rzeczywistą, musi być

Dla t=0 jest x=y=0; dla t=1 jest x=2, y=1,5

Przypadek (3)

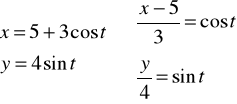
podnosimy stronami do kwadratu i dodajemy:

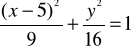
Przypadek (4)

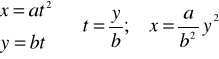
Przypadek (5)

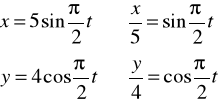
podnosimy stronami do kwadratu i dodajemy

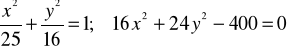
Przypadek (6)

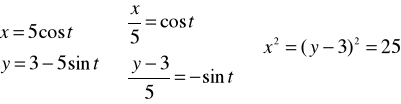
Przypadek (7)

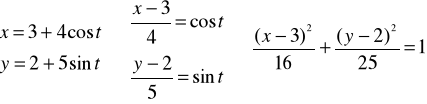
Przypadek (8)

z= 3cos(π/8+πt), y+4sin(π/4+πt)

Z drugiego równania:

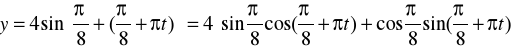
Z pierwszego równania:

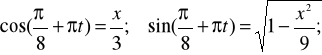
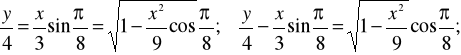
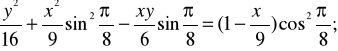
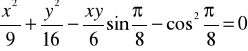
ZAD317 Korba OA obraca się ze stałą prędkością kątową
^-1. Długość OA = AB = 80cm. Znaleźć równanie ruchu i toru środka M korbowodu AB oraz równanie ruchu wodzika B , jeśli w chwili początkowej wodzik znajduje się w skrajnym prawym położeniu . Osie współrzędnych pokazano na rysunku.

Rozwiązanie:

Oznaczmy: OA=AB=2l=80cm. Dla punktu m z rysunku;

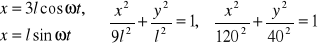
-elipsa

Dla wodzika (punkt B): x=4lcosωt, y=0; x=160cos10t

ZAD325 Punkt wykonuje drgania harmoniczne w myśl równania x= a sin kt. Obliczyć amplitudę a oraz częstość kołową k drgań, jeżeli dla x=x₁ mamy v=v₁ dla x=x₂ zaś v=v₂

Rozwiązanie:

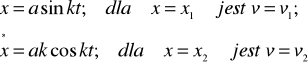
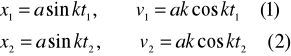
Równania każdej pary (1) i (2) podnosimy do kwadratu i dodajemy stronami skąd

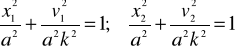
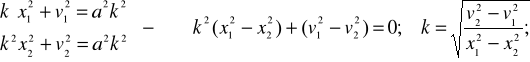
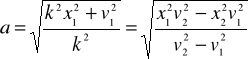
ZAD338 Krople wody wyciekają z otworu pionowej rurki w odstępach czasu 0,1s i spadają z przyśpieszeniem 981cm/s²_. Obliczyć odległość między pierwszą a następna kroplą po 1s od chwili oderwania się pierwszej kropli.

Rozwiązanie:

Odległość
; zatem t₂=t₁-0,1s=1-0,1=0,9s

d=981*1²/2-981*0,9²/2=93,2cm

ZAD339 Droga przemywana przez tramwaj podczas rozbiegu jest proporcjonalną do trzeciej potęgi czasu. W ciągu pierwszej minuty tramwaj przebywa drogę 90m. Znaleźć prędkość i przyśpieszenie w chwili t= 0 i t= 5 oraz wykreślić krzywą drogi, krzywą prędkości i krzywą przyśpieszenia .

Rozwiązanie:

s=kt³, 90=k*1³ , k=90m/min³; v=ds/dt=3kt²; p=d²s/dt²=6kt

dla t=0 jest v₀=0; p₀=0 dla t=5s=1/12min jest v₅=3*90*1/144=15/8m/min,

p₅=6*90*1/12=45m/min²

ZAD352 Ruch punktu określają równania x= a(e^kt+e^-kt), y= a(e^kt-e^-kt), gdzie a i k są stałe. Znaleźć równanie toru oraz prędkości i przyśpieszenie punktu jako funkcje promienia wodzącego r=

Rozwiązanie:

Dane:
podnosimy do kwadratu i odejmujemy stronami:

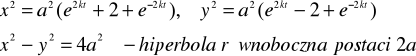
Ponieważ dla t-0 jest x= 2a, y=0 (punkt A na rysunku), a następnie x>0, y>0, więc torem ruchu jest gałąź hiperboli znajdująca się w I ćwiartce układu współrzędnych. Znajdujemy prędkość:

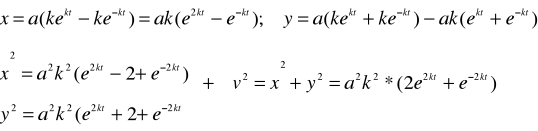
Promień wodzący punktu w układzie biegunowym ρ=r dany jest wzorem

Podobnie:

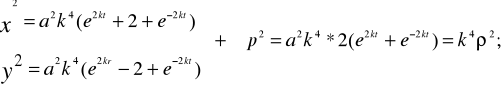
ZAD359. Znaleźć tor punktu M znajdującego się na korbowodzie mechanizmu korbowego, jeżeli r = l = 60 cm, MB =

(gdzie t w sekundach). Obliczyć również prędkość, przyśpieszenie i promień krzywizny punktu w chwili gdy
.

Rozwiązanie:

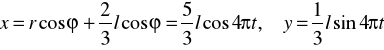
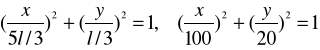
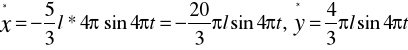
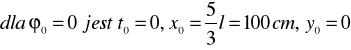
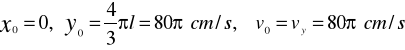
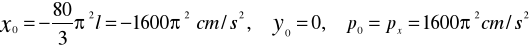
Całkowite przyśpieszenie p₀ dla t₀ jest prostopadłe do v₀, a więc przyśpieszenie p₀ jest przyspieszeniem normalnym p_n0; zatem

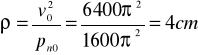
ZAD369 Wyznaczyć ruch pocisku (równania ruchu, tor, wysokość i zasięgstrzału) jeżeli wiadomo, że przyśpieszenie jego p=g = 9,81m/s² jest stałe skierowane pionowo w dół, prędkość początkowa zaś v₀₌1000m/s tworzy z poziomem kąt
.

Rozwiązania:

ZAD374 Ruch punktu określono we współrzędnych biegunowych równaniami: r = ae^kt i
, gdzie a i k są stałymi. Znaleźć równanie toru oraz wyznaczyć prędkość, przyśpieszenie i promień krzywizny toru jako funkcje promienia wodzącego r.

Rozwiązanie:

Równanie toru

Prędkość całkowita
tworzy z promieniem kąt
gdyż

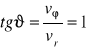
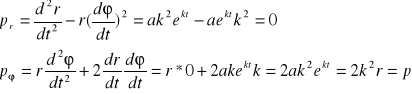
Przyspieszenie ma tylko składową prostopadłą do promienia, a więc tworzy z kierunkiem prędkości punktu kąt

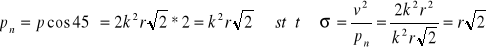
ZAD379 Wał zaczyna się obracać ze stałym przyśpieszeniem i w ciągu pierwszych 5 s wykonuje 12,5 obrotu. Jaką prędkość kątową ma on po upływie tych 5s?

Rozwiązanie:

ponieważ

ZAD388 Punkt A na obwodzie koła porusza się z prędkością 50cm/s, a pewien punkt B leżący na tym samym promieniu co punkt A w odległości AB = 20cmporusza się z prędkością 10cm/s .Obliczyć prędkość kątową
i średnicę koła d.

Rozwiązanie:

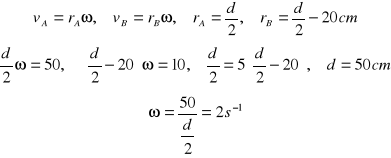
ZAD390 Znaleźć poziomą prędkość v, jaką trzeba nadać ciału znajdującemu się na równiku, aby poruszając się wokół Ziemi po równiku miało przyśpieszenie swobodnego spadku. Obliczyć także czas t, po którego upływie ciało powróci do położenia początkowego. Promień Ziemi R=637*10⁶cm,a przyśpieszenie ziemskie na równiku g=978cm/s²

Rozwiązanie:

Czas obiegu ziemi:

t=40000/7,9=5060s=1,4h

ZAD392 Wał A o promieniu R=10cm obracany jest za pomocą ciężarka P przywiązanego do niego na lince. Ruch ciężarka wyraża się równaniem x=100t², gdzie x jest odległością ciężarka od prostej poziomej 00₁ wyrażoną w centymetrach, t zaś wyrażone jest w sekundach . Obliczyć prędkość kątową
i przyśpieszenie kątowe
wał, a także całkowite przyśpieszenie p punktu leżącego na powierzchni wału - w chwili t. (Rysunek powyżej)

Rozwiązanie:

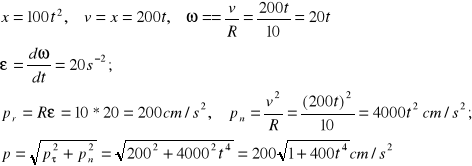
ZAD431 Brzegi rzeki są równoległe. Łódź odpłynąwszy od punktu A utrzymuje kurs prostopadły do brzegów i dopływa po 10 min do drugiego brzegu w punkcie C, leżącym o 120m poniżej punktu A, z biegiem rzeki. Aby dopłynąć z punktu A do punktu B leżącego na prostej AB prostopadłej do brzegów, łódź musi utrzymywać kurs przeciw prądowi pod pewnym kątem do prostej AB. W tym przypadku łódź osiągnie brzeg przeciwny po 12,5 min. Obliczyć szerokość rzeki l, względną prędkość w łódki w odniesieniu do wody i prędkość wody w rzece u.

Rozwiązanie:

Oznaczamy prędkość łodzi przez w (prędkość względna),prędkość wody w rzece przez u(prędkość unoszenia),a prędkość wypadkową przez v=u+w. W pierwszym przypadku:BC=ut₁, 120=u*10, u=12m/min. Szerokość rzeki AB

m.W drugim przypadku
-prędkość bezwzględna v₂ jest prostopadła do brzegów rzeki.Zatem

AB=

ZAD433 W mechanizmie korbowym z jarzmem BC poruszającym się ruchem postępowym korba OA o długości l = 200mm obraca się ze stałą prędkością kątową odpowiadającą n=90obr/min. Koniec A złączony jest przegubowo z kamieniem ślizgającym się w wycięciu jarzma i nadaje jarzmu ruch posuwisto-zwrotny. Obliczyć prędkość v jarzma w chwili, gdy korba tworzy z osią kąt x OA=

Rozwiązanie:

Prędkość końca korby A jest
.Prędkość ruchu postępowego jarzma jest równa prędkośći
:

ZAD438 W mechanizmie przedstawionym na rysunku przy ruchu korby OC dookoła osi O, prostopadłej do płaszczyzny rysunku, suwak A poruszający się wzdłuż korby OC wprawia w ruch pręt AB poruszający się w pionowej prowadnicy K. Odległość OK=l. Określić prędkość ruchu suwaka A względem korby OC jako funkcję prędkości kątowej
i kąta obrotu
korby.

Rozwiązanie:

ZAD451 Koło zębate o promieniu R=0,5m jest zaciśnięte między dwiema równoległymi listewkami ślizgającymi się w jednym, kierunku z przyśpieszeniami p₁=1,5m/s² i p₂=2,5m/s^2. Wyznaczyć przyśpieszenie p₀ środka koła O i kątowe przyśpieszenie koła. Ruch postępowy układu osi O
wraz ze środkiem koła przyjąć jako ruch unoszenia.

Rozwiązanie:

ZAD486 Po torze biegnącym wzdłuż równoleżnika porusza się parowóz z prędkością w=20m/s z zachodu na wschód. Obliczyć przyspieszenie Coriolisa dla parowozu.

Rozwiązanie:

Prędkość względna
.Przyspieszenia Coriolisa
Przyspieszenie to leży na promieniu równoleżnika, jeśli parowóz porusza się w kierunku z zachodu na wschód, to p_c zawrócone jest ku osi Ziemi.

ZAD501 Pręt AB o długości 1m porusza się opierając cały czas końcami o dwie wzajemnie prostopadłe proste Ox i Oy. Obliczyć współrzędne x i y chwilowego środka obrotu w chwili, gdy

Rozwiązanie:

Ponieważ prędkość punktu A leży na osi y a prędkość punktu B na osi x więc chwilowy środek obrotu C leży na przesunięciu prostopadłych wystawionych w punkcie A i B do odpowiednich osi.Zatem

ZAD506 Prosta AB porusza się w płaszczyźnie rysunku. W pewnej chwili prędkość v_A punktu A tworzy z prostą AB kąt
i wynosi 180cm/s; kierunek prędkości punktu B w tej chwili pokrywa się z kierunkiem prostej AB. Obliczyć prędkość v_B punktu B.

Rozwiązanie:

Z twierdzenia:rzuty prędkości wszystkich punktów prostej sztywnej na tę prostą mają jednakową wartość wynika że

ZAD508 Krążek o promieniu R toczy się bez poślizgu po poziomej płaszczyźnie HH. Na środkowej, walcowej części krążka o promieniu r nawinięta jest linka, której koniec B ma prędkość u w kierunku poziomym. Wyznaczyć prędkość v przemieszczania się osi krążka.

Rozwiązanie:

Chwilowym środkiem obrotu koła jest punkt C, w którym koło styka się z płaszczyzną HH. Stąd:

ZAD519 Jednorodny pręt spada w płaszczyźnie pionowej pod wpływem siły ciężkości , obracając się ze stałą prędkością kątową
^-1 dokoła osi prostopadłej do płaszczyzny spadania. W chwili początkowej prędkość środka ciężkości równa się zeru, a pręt ma położenie pionowe. Wyznaczyć prędkość punktów A i B w chwili gdy pręt obrócił się o kąt
rad, jeśli AB=66cm.

Rozwiązanie:

Czas spadania na odcinku C₀C:

Prędkość punktu C
Chwilowy środek obrotu S pręta AB leży na prostopadłej CS do prędkośći v_c w odległośći
.Z trójkątów SAC i SBC:

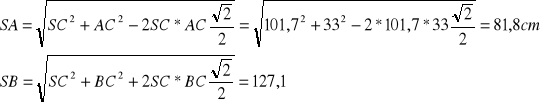
Prędkości całkowite punktów A i B są prostopadłe, odpowiednio, do SA i SB i mają wartości

ZAD637 Dźwig o ciężarze 280kG opuszcza się w szybie ruchem jednostajnie przyśpieszonym i przebywa w początkowych 10s drogę 35m. Wyznaczyć napięcie liny na której wisi dźwig.

Rozwiązanie:

Na podstawie drugiego prawa Newtona
gdzie T kG-siła w linie;Q/g -masa ciężaru wiszącego na linie(w technicznych jednostkach masy); p m/s²-przyspieszenie, które znajdziemy z zależności:

Zatem:

ZAD641Ciało o ciężarze 3kG uwiązane jest na lince o długości 1m i zatacza okrąg koła w płaszczyźnie pionowej . Obliczyć najmniejszą prędkość kątową
ciała, przy której linka ulegnie zerwaniu, jeśli siła rozrywająca linkę wynosi 9kG.

Rozwiązanie:

w górnym punkcie okręgu jest
,
w dolnym
a więc napięcie w linie jest większe w dolnym położeniu:

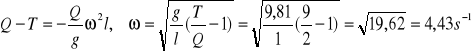
ZAD643 W wagonie pociągu poruszającego się po krzywiźnie z prędkością 72km/h ważymy dane ciało na wadze sprężynowej; ciężar ciała wynosi 5kG, waga zaś wykazała 5,1kG. Obliczyć promień zakrętu pomijając masę wagi.

Rozwiązanie:

Rzuty równania dynamicznego ruchu na osie x,z:

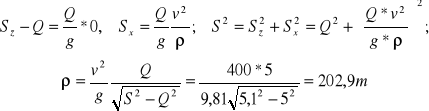
ZAD648 Nadwozie tramwaju wraz z ładunkiem ma ciężar Q₁=10T, podwozie z kołami Q=1O T. Wyznaczyć największą i najmniejszą siłę wywieraną przez tramwaj na szyny poziomego prostoliniowego toru, jeśli tramwaj wykonuje pionowe drgania harmoniczne według równania x=2sin10
(x wyrażamy w centymetrach)

Rozwiązanie:

Nadwozie wykonuje rucy pionowe według równania x=2sin10τ cm, z któregowynika, że maksymalneodchylenia od położenia średniego wynoszą ±2 cm; prędkość ruchu

Przyspieszenie jest proporcjonalne do wychyleniai ma zwrot przeciwny, a więc w skrajnym dolnym położeniu nadwozia

cm/s² zwrócone jest w górę, w skrajnym górnym
cm/s² - w dół. Odpowiednie siły F oddziaływania między podwoziem i nadwoziem znajdziemy z

zależności

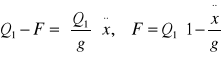
Dla położenia dolnego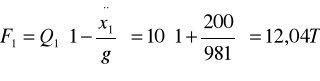

ZAD655 Wagonik kolejki liniowej o ciężarze Q=700kG zjeżdża po torze nachylonym pod kątem a=
i ma prędkość v =1,6m/s. Wyznaczyć siłę w linie przy jednostajnym opuszczaniu i przy zatrzymywaniu wagonika, jeśli czas hamowania t= 4s, a współczynnik oporów ruchu f=0,015 w stosunku do siły prostopadłej do linii.

Rozwiązanie:

Równanie dla ruchu wzdłuż liny:

opory ruchu R=fQcosα; podczas hamowania przyspieszenie p=(0-v)/t=-1,6/4=-0,4 m/s²

Podczas ruchu jednostajnego p=0

Podczas ruchu z przyspieszeniem p=-0,4 m/s² jest

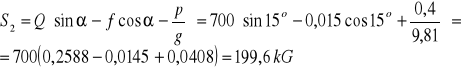
ZAD663 Samolot w locie nurkowym pionowo w dół osiągnął prędkość 1000km/h, po czym lotnik zaczął wyrównywać lot w płaszczyźnie pionowej po ruchu okręgu o promieniu R=600 . Ciężar lotnika wynosi 80kG. Z jaką największą siłą lotnik dociskany jest do siedzenia?

Rozwiązanie:

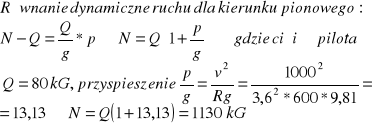
ZAD664 Jaki ciężar będzie miało na księżycu ciało o ciężarze 1kG, jeśli przyśpieszenie wynosi tam j=1,7m/s²? Jaki ciężar będzie miało na słońcu ciało o ciężarze 1kG, jeśli przyśpieszenie wynosi tam j=270m/s²?

Rozwiązanie:

Ciężar ciała jest równy iloczynowi masy tego ciała przez doznawane przyspieszenie:
;

jeśli masa m jest wyrażona w technicznych jednostkach masy (m=Q_z/g, gdzie Q_z- ciężar w Kg na powierzchni ziemi, g- przyspieszenie ziemskie), to ciężar Q wyraża się w Kg.

Ciężar na księżycu:

Ciężar na słońcu:

ZAD756 Obliczyć najmniejszą pracę, którą należy wykonać, aby podnieść o 5m ciężar 2T ciągnąc go po równi pochyłej tworzącej z poziomem kąt
.

Rozwiązanie:

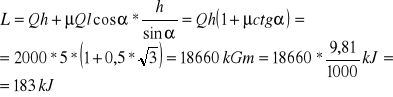
ZAD762 Obliczyć pracę jaką trzeba wykonać przy podnoszeniu ciężaru 20kG po równi pochyłej na odległość 6m , jeżeli kąt zawarty między równią a poziomem wynosi
a współczynnik tarcia 0,01.

Rozwiązanie:

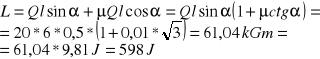
ZAD776 Pociąg jedzie z prę

dkością 38km/h w dół po stoku nachylonym do poziomu pod kątem a = 0,008. W pewnej chwili maszynista spostrzegłszy niebezpieczeństwo zaczyna hamować pociąg. Opór hamowania i tarcia w łożyskach wynosi 0,1 ciężaru pociągu. Obliczyć w jakiej odległości i po jakim czasie pociąg zatrzyma się. Przyjąć sin a = a

Rozwiązanie:

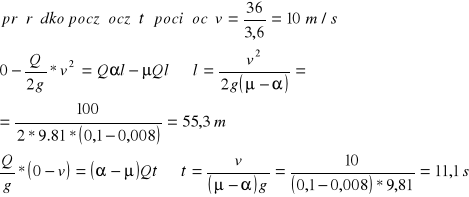
ZAD780 Gwóźdź wbijany w ścianę stawia opór R=70kG. Przy każdym uderzeniu młotka gwóźdź zagłębia się w ścianę l= 0,15cm. Obliczyć ciężar młotka P, jeżeli w chwili uderzenia o główkę gwoździa ma on prędkość v1,25m/s.

Rozwiązanie:

ZAD798 Ciało o ciężarze 1kG wisi na lince o długości 50cm umocowanej w nieruchomym punkcie O. W położeniu początkowym ciało jest odchylone od pionu o kąt
i ma prędkość v₀₌210cm/s skierowaną w dół w płaszczyźnie pionowej prostopadle do linki.

Rozwiązanie:

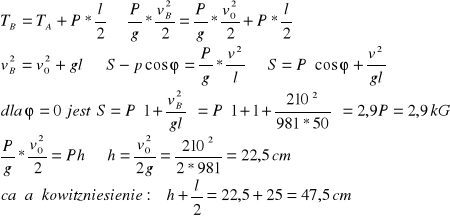
ZAD806 Wahadło sferyczne składa się z nici OM o długości l zamocowanej jednym końcem w nieruchomym punkcie O i z punktu materialnego M o ciężarze P przymocowanego do drugiego końca nici. Punkt M wychylony jest z położenia równowagi tak, że jego współrzędne dla t=0 są x=x₀, y=0, z=z₀, a składowe jego prędkości początkowej wynoszą: x₀=0, y₀=v_0, ż₀=0. Dla jakich warunków początkowych punkt M będzie opisywał w płaszczyźnie poziomej okrąg i jaki będzie okres obiegu punktu po tym okręgu?

Rozwiązanie:

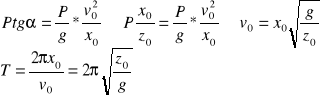
ZAD821 Wzdłuż jakiej krzywej płaskiej należy zgiąć rurkę , aby kulka umieszczona w dowolnym punkcie rurki pozostała w równowadze, jeżeli rurka obraca się z prędkością
dokoła Oy? Pominąć tarcie.

Rozwiązanie:

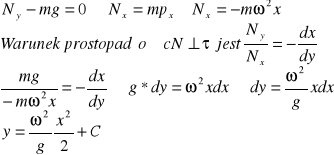
ZAD830 Wyznaczyć okres drgań własnych fundamentu maszyny ustawionego na podłożu sprężystym , jeżeli ciężar fundamentu wraz z maszyną wynosi 90T, pole powierzchni podstawy S=15m², sztywność podłoża c=
, gdzie
=3kG /cm³ jest sztywnością właściwą podłoża.

Rozwiązanie:

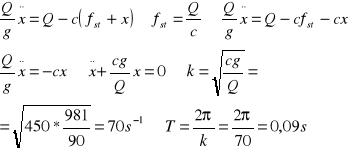
ZAD925 Trzy ciała, każde o ciężarze P połączone są nieważką nierozciągliwą linka, przerzuconą przez nieruchomy krążek A. Dwa ciała leżą na gładkiej płaszczyźnie poziomej, a trzecie wisi swobodnie. Obliczyć przyśpieszenie układu i siłę w przekroju ab linki.

Rozwiązanie:

Dane: u=o

Rozw: a=(Pg-uP₁g-uP₂g)/(P₁+P₂+P)=1/3*g

F=m*a m=P/g N=p/g*1/3*g=P/3

ZAD926 Przez krążek przerzucona jest wiotka nierozciągliwa linka, do której końców przymocowano ciała: M₁ o ciężarze P₁ i M₂(przy czym P₂>P₁). Znaleźć przyśpieszenie p ciał oraz siłę T w lince z pominięciem masy krążka i linki.

Rozwiązanie:

Rozw: P₁>P₂ a=p=g*(P₂-P₁)/(p₁+p₂)

T=2P₁P₂/(P₁+P₂)

ZAD934 Ciało A o ciężarze P zsuwa się po gładkiej równi pochyłej tworzącej z poziomem kąt a. Ciało to za pośrednictwem nieważkiej i nierozciągliwej linki wprawia w ruch bęben B o ciężarze Q i promieniu r. Obliczyć przyśpieszenie kątowe bębna, który jest jednorodnym walcem kołowym. Masę krążka C pominąć.,

Rozwiązanie:

Dane: P,α,Q,r Szukane: ε=?

I: Psinα-B-S=0

S=Psinα-B=Psinα-P/g*a

S=P(sinα-a/g)a=εr

II: I0*ε=S*r I0=mr²/2=Qr²/2g

III: Qr²/2g*ε+P/g*ε*r²=Psinαr

ε(Qr/2g+Pr/g)=Psinα

ε=Psinα/(Qr/2g+Pr/g)=

=Psinα/(Qr*2P*r/2g)=2gPsinα/(Qr+2Pr)

ε=2gPsinα/(r*(Q+2P))

ZAD941 Walec A o ciężarze Q stacza się bez poślizgu po równi pochyłej podnosząc za pośrednictwem nieważkiej i nierozciągliwej linki przerzuconej przez krążek B ciało C o ciężarze P. Krążek obraca się dokoła nieruchomej osi O, prostopadłej do płaszczyzny , w której leży linka. Walec A i blok B są jednorodnymi krążkami o jednakowym promieniu i ciężarze. Równia pochyła tworzy z poziomem kąt a. Obliczyć przyśpieszenie osi walca.

Rozwiązanie:

I: S₁-B-P=0 B+P-S₁=0

II: I0*ε+S₁*r-S₁*r=0 I0=mr²/2=Q/g*r²/2

III: I0*ε+S₂*r-Qrsinα=0 Ic=I0+mr²

S₂*r=Qrsinα-G/r*3/2*mr²=mr²/2+ mr²=3/2*mr² =>S₂=Qsinα-3/2*am

S₁=P+P/g*a

ZIII: Qr/2g*Q/r+rp+rP/g*a-Qsinαr+3/2*ram=0

Q/r*Qr/2g+raP/g-3/2*ram=Qsinαr-rp

a=(Q/2g+p/g-3/2*Q/g)=Qsinα-p//*g

a=(2Q+P)=g(asinα-p)

ZAD1091 Ciężar A o wartości P opada zawieszony na nieważkiej nierozciągliwej lince przeciągniętej przez blok D i nawiniętej na bęben B. Na bębnie tym osadzone jest sztywno koło C toczące się bez poślizgu po poziomej szynie. Bęben B ma promień r, koło C - promień R. Ich wspólny ciężar wynosi Q, a ramię bezwładności względem osi poziomej O równa się
. Wyznaczyć przyśpieszenie ciężaru A.

Rozwiązanie:

Dane: P,v,R,Q,g
Szukane: a=?

I: P-B-S=0 => S=P-B =>

S=P-P/g*a =>S=P(1-a/g)

II: IE*ε=S(R+r) =>

IE=g²m+m(g²+R²)=Q/g(ρ²+R²)

ZII: Q/g(ρ²+R²)*a/(R+r)= P(1-a/g)*(R+r)//:(R+r)

Q*(ρ²+R²)/(g*(R+r)²)*a+(P*a)/g=P

a*((Q*(ρ²+R²))/(g*(R+r)²)+P/g)=P//:()

a=p/((Q*(ρ²+R²))/(g*(R+r) ²)+P/g)

---