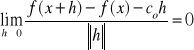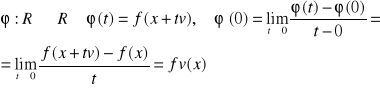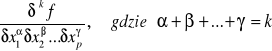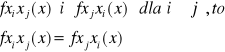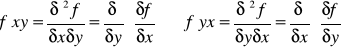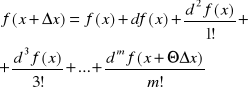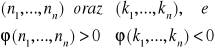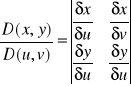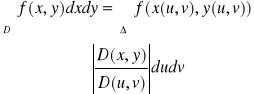II Funkcje wielu zmiennych. 1. Odległość i norma euklidesowa. Odległość punktów: Własności odległości: - d (x,y) = 0 ⇔ x = y - d (x,y) = d (y,x) - d (x,z) ≤ d (x,y) + d (y,z) - d (x,y) = || x - y || Norma euklidesowa (dług. wektora) Własności normy: - ||x|| = 0 ⇔ x = Θ = (0,0,....,0) - ||α|| = |α| ||x|| α ∈ R - ||x+y|| ≤ ||x|| + ||y|| nierówność trójkąta 2. Punkty wewnętrzne i brzegowe, zbiór otwarty i zamknięty. Mówimy, że a ⊂ R^n jest punktem wewnętrznym zbioru A ⊂ R^n jeżeli istnieje takie r > 0, że K (a,r) ⊂ A. Wnętrzem zbioru nazywamy zbiór wszystkich jego punktów wewnętrznych. K (a,r) - otoczenie punktu a o promieniu r K ( a,r) \ {a} - sąsiedztwo pkt. a o promieniu r.	Punkt a ⊂ R^n jest punktem brzegowym zbioru A ⊂ R^n jeżeli każde otoczenie punktu „a” zawiera zarówno punkty zbioru A jak i punkty nie należące do zbioru A. Zbiór A ⊂ R^n nazywa się otwartym jeżeli każdy punkt tego zbiory jest jego punktem wewnętrznym. Wnętrze każdego zbioru jest zbiorem otwartym. Zbiór A ⊂ R^n nazywamy domkniętym jeżeli R^n \ a jest zbiorem otwartym. 3. Punkt skupienia zbioru. Punkt a ⊂ R^n nazywamy punktem skupienia zbioru A ⊂ R^n jeżeli każde sąsiedztwo punktu a zawiera punkty zbioru A. Punkt skupienia zbioru nie musi do niego należeć. 4. Granica ciągu R^n. Zakładam: Mówimy że : jeżeli Tw.	5.Granica funkcji n zmiennych. Zakładam A ⊂ R^n , a - pkt. skupienia zbioru A f: A \ {a} → R f(x), f(x1, x2, ... , xn). Mówimy, że jeżeli dla każdego ciągu {x^(m)} argumentów funkcji f różnych od „a” i takiego, że: 6. Ciągłość funkcji n zmiennych. Zakładam A ⊂ R^n , a ∈ A, a - pkt skupienia A, Funkcja f: A→R jest ciągła w punkcie a, jeżeli 7. Zbiór spójny, zwarty, obszar. Zbiór A ⊂ R^n nazywa się spójnym jeżeli każde jego dwa punkty można połączyć łamaną zawartą w zbiorze A. Zbiór A ⊂ R^n jest zwarty jeśli jest domknięty i ograniczony. Obszarem nazywa się zbiór otwarty i spójny. 8. Różniczkowalność f n-zmiennych Niech U ⊂ R^n będzie zbiorem otwartym oraz x ∈ U. Mówimy, że funkcja f: U→R jest różniczkowalna w pkt. x jeżeli istnieje taki wektor c = (c1,c2,...,cn) ∈ R^n ,że:	9. Pochodna kierunkowa. U ⊂ R^n zbiór otwary, x ∈U, wektor v ∈ R^n, v ≠ Θ. Mówimy, że funkcja f: U→R ma w pkt. x pochodną w kierunku wektora v jeżeli istnieje granica skończona: 10.Poczodne cząstkowe I rzędu i k rzędu. Niech z = f (x,y). Pochodną cząstkową rzędu I funkcji z w punkcie (x0,y0) względem zmiennej x nazywamy granicę ( o ile istnieje): Pochodną cząstkową rzędy k funkcji f (x1,x2,...,xn) nazywamy pochodną cząstkową (jeżeli istnieje) pochodnej cząstkowej rzędu k-1 i oznacza się:	11. Zależność różniczki funkcji i poch. cząstkowej. U ⊂ R^n jest zbiorem otwartym x = (x1,x2,...,xn) ∈U, f: U→R. Jeżeli funkcja f jest różniczkowalna w punkcie x, to ma w tum punkcie pochodną cząstkową względem każdej zmiennej. 12. Różniczkowanie funkcji złożonej. g(x,y),h(x,y) określone w zbiorze A, (g(x,y),h(x,y)) ⊂ B, funkcja f(v,u) określona w B. Jeżeli funkcje g(x,y) i h(x,y) mają pochodne cząstkowe w punkcie (x0,y0) a funkcja f(u,v) ma pochodne cząstkowe f ` u i f ` v ciągłe w otoczeniu pkt. (u0,v0) gdzie uo = g(x0,y0), v0 = h(x0,y0) to funkcja złożona F(x,y) = f(g(x,y),h(x,y)) ma pochodne cząstkowe w pkt. (x0,y0) przy czym: 13. Różniczka zupełna. Wyrażenie: nazywamy różniczką zupełną funkcji f w punkcie x. Zastosowanie:	15. Pochodne mieszane tw. Schwarza. Tw. f: U→R, U ⊂ R^n jest zbiorem otwartym. Jeżeli funkcja f ma w pkt. x∈U ciągłe pochodne cząstkowe: Pochodne cząstkowe mieszane: niech f(x,y) określona w obszarze D. Zakładam istnienie pochodnych cząstkowych tej funkcji f`(x,y) i f`(x,y) 16. Różniczka zupełna II rzędu. f: U→R; U ⊂ R^n ; x = (x1,x2,...,xn) ∈U; Zakładam że istnieją pochodne mieszane II rzędu i są ciągłe w pkt. x: Przy stałych dx1,...,dxn df(x) jest funkcją n zmiennych:
17. Wzór Taylora dla funkcji wielu zmiennych. Zakładam że U ⊂ R^n jest zbiorem otwartym, a funkcja f: U→R ma w pkt. x = (x1,x2,...,xn) ∈U ciągłe pochodne cząstkowe do m -0 tego rzedu włącznie. Oznacza to, że funkcja f jest w pkt. x klasy C^m. Wówczas dla przyrostu Δx = (Δx1, Δx2,...,Δxn) takiego że x + Δx ∈ U istnieje liczba Θ ∈ (0,1) taka, że: 18. Forma kwadratowa. Formą kwadratową n zmiennych h1,h2,...,hn nazywamy każdą funkcję postaci : gdzie przynajmniej jedna aij ≠ 0 oraz aij = aji dla wszystkich i,j.	19. Dodatnia, ujemna określoność form kwadratowych. Formę kwadratową n zmiennych ϕ (n1,...,nn) nazywamy: - dodatnie określoną jeżeli: - ujemnie określoną, jeżeli: - nieokreśloną, jeśli istnieją takie: 19a. Kryterium Sylvestra. Niech ϕ (n1,...,nn) będzie formą kwadratową o macierzy A. Forma ϕ jest: - dodatnio określona ⇔ Δ1 > 0, Δ2 > 0, ... , Δn > 0 - ujemnie określona ⇔ Δ1 < 0, Δ2 > 0, Δ3 < 0, ... ,(-1)^n Δn > 0 - nieokreślona forma kwadratowa ϕ (n1,n2) = an^21 + 2bn1n2 + cn2^2 o macierzy A=[^ab^bc] jest wówczas jeżeli det A = ac-b^2 <0 20. Extremum lokalne funkcji n zmiennych. Funkcja f: A→R, gdzie A ⊂ R^n ma w pkt. a ∈A min (max) lokalne o ile istnieje taka kula K(a,r) że dla każdego x∈A i K(a,r) zachodzi nierówność:	20. WK istnienia extremum lokalnego. Zakładam f: U→R, U ⊂ R^n jest zbiorem otwartym. Funkcja f ma w zbiorze U pochodne cząstkowe. Jeżeli funkcja f ma w pkt. a ∈ U extremum lokalne, to ***: 21. WW istnienia extremum. Zakładam, że U ⊂ R^n jest zbiorem otwartym, f: U→R jest klasy C^2. Istnieje dla a ∈ U wzór*** wtedy: - jeżeli d^2 f (a) jest formą dodatnie określoną, to f ma w pkt. a min - jeżeli d^2 f (a) jest formą ujemnie określoną, to f ma w pkt. a max - jeżeli d^2 f (a) jest formą nieokreśloną , to f nie ma extremum.	III. Całki podwójne. 1. Definicja całki podwójnej. Określenia: niech D będzie obszarem regularnym, f(x,y) - funkcją ograniczoną w D. P będzie prostokątem zawierającym D. Oznaczam przez πn podział prostokąta P na mn prost. cześciowych z których: zawierają pkt. obszaru D. σi^(n) oznacza pole prostokąta Pi^(n); Ai^(n)(xi^(n), yi^(n)) oznacza dowolny pkt. obszaru D należący do prostokąta. δn najdłuższy z boków prostokątów P1^(n), P2^(n), Pmn^(n),a Sn suma : TW. Jeżeli dla każdego ciągu podziałów πn takiego że granica δn przy n →∞ równa jest 0, ciąg * jest zbieżny do tej samej liczby bez względu na wybór punktów Ai^(n) , to mówimy, że funkcja f(x,y) jest całkowalna w obszarze D a wspólną granicę ciągów * nazywamy całką podwójną funkcji f(x,y) w obszarze D i oznacz: interpretacja: objętość bryły ograniczonej obszarem D.	9.Zmiana zmiennych w całce podwójnej. Niech przekształcenie 1) x = x (u,v), y = y (u,v) odwzorowuje obszar regularny domknięty Δ w płaszczy. u i v na obszar regularny domknięty D w płaszczy. x i y. Jeżeli funkcje x,y są klasy C^1 to wyrażenie : nazywamy jakobianem przekształcenia 1). Jeżeli w przekształceniu 1): - funkcje x(u,v), y(u,v) są klasy C^1 w pewnym zbiorze otwartym U zawierającym obszar regularny Δ, - D - obszar regularny - Wnętrze obszaru Δ przechodzi w przekształcenie x = x (u,v), y = y (u,v) na wnętrze obszaru D, - Jakobian różny od zera dla każdych (u,v) ∈ U - f(x,y) jest ciągła w D to zachodzi wzór:	10. Zamiana zmiennych na biegunowe. Założenia punktu9. x = ρcosϕ, y = ρsinϕ, mamy: 11. Własności całek podwójnych. Założenia: D1,D2,D - obszary normalne. - - jeżeli D1 D2 nie mają wspólnych pkt. wewnętrznych, to:
IV. Całki krzywoliniowe. 1. Całka krzywoliniowa nieskierowana. Założenia: x = x(t), y = y(t), x,y klasy C^1 Ai (x(ti),y(ti)) , i=0,1,...,n -punkty na łuku L. Długość łuku: Punkty pośrednie łuku L Ci (x(ci),y(ci) i=1,...,n. Suma całk.: gdzie f jest funkcją II zmiennych określoną na łuku L. TW. Jeżeli dla każdego ciągu normalnego (Δn) podziału przedziału [α,β] istnieje granica skończona limn→∞ Sn niezależna od wyboru pkt. pośrednich c1, ...,cn to nazywamy ją całką krzywoliniową nieskierowaną funkcji po łuku L i oznaczamy:

---