Dystrybuanta rozkładu warunkowego zmiennej losowej Y przy warunku, że zmienna X=x wyraża się wzorem 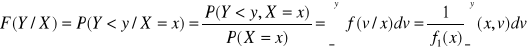
WYKŁAD 7
(by elle)
Dystrybuanta rozkładu warunkowego zmiennej losowej Y przy warunku, że zmienna X=x wyraża się wzorem 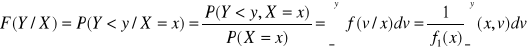
Wartość oczekiwana rozkładu warunkowego zmiennej losowej (warunkowa).
Niech (X,Y) jest dwuwymiarową zmienną losową typu skokowego
1. ![]()
przy założeniu, że ![]()
![]()
przy założeniu, że ![]()
Niech (X,Y) jest dwuwymiarową zmienną losową typu ciągłego
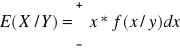
przy założeniu, 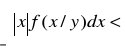
(że jest skończona co do wartości bezwzględnej )
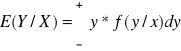
przy założeniu,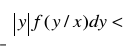
(że jest skończona co do wartości bezwzględnej)
Wariancja rozkładu warunkowego
Niech (X,Y) jest dwuwymiarową zmienną losową typu skokowego
![]()
przy założeniu, że ![]()
![]()
przy założeniu, że ![]()
Niech (X,Y) jest dwuwymiarową zmienną typu ciągłego
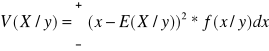
przy założeniu ![]()
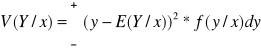
przy założeniu ![]()
Charakterystyki liczbowe (momenty) wielowymiarowej zmiennej liczbowej
momenty zwykłe
Momentem zwykłym rzędu r1+r2 +…+rn (ri![]()
No; i=1,2…n) zmiennej losowej wielowymiarowej (x1,x2,…xn) nazywamy wyrażenie ![]()
o ile one istnieje .
Szczególny przypadek m=2 - dwuwymiarowa zmienna losowa
Momentem zwykłym rzędu r +s (r, s![]()
No) dwuwymiarowej zmiennej losowej (X,Y) nazywamy wyrażenie jeżeli ono istnieje ![]()
Jeżeli (X,Y) jest dwuwymiarową zmienną typu losową typu skokowego to ![]()
przy założeniu ![]()
r, s ![]()
N0
Jeżeli (X,Y) jest dwuwymiarową zmienną losową typu ciągłego to 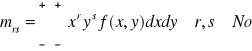
przy założeniu 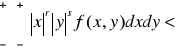
UWAGA!!
![]()
moment zwykły rzędu r w rozkładzie brzegowym zmiennej losowej x(r![]()
N)
![]()
wartość oczekiwana (przeciętna) zmiennej x
![]()
moment zwykły rzędu s w rozkładzie brzegowym zmiennej losowej typu y
![]()
wartość oczekiwana zmiennej losowej y
momenty centralne
Momentem centralnym rzędu r1+r2+…+rn zmiennej losowej (x1,x2,…xn) nazywamy wyrażenie jeżeli ono istnieje ![]()
Szczególny przypadek n=2
Momentem centralnym rzędu r+s (r,s ![]()
N0) dwuwymiarowej zmiennej losowej (X,Y) nazywamy wyrażenie (jeśli ono istnieje)
![]()
Jeżeli (X,Y) jest dwuwymiarową zmienną losową typu skokowego, to ![]()
przy założeniu , że![]()
r,s![]()
N0
Jeżeli (X,Y) jest dwuwymiarową zmienną losową typu ciągłego, to 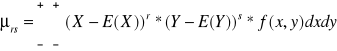
przy założeniu, że 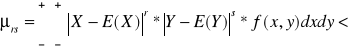
UWAGA!!
![]()
wariancja w rozkładzie brzegowym zmiennej losowej X
![]()
wariancja w rozkładzie brzegowym zmiennej Y
Jeżeli dla zmiennej losowej (x1,x2,…xn) dla ustalonych i oraz k , ri=1, rk=1, rj=0 dla j≠i, j≠k to moment centralny rzędu 1+1 nazywamy kowariancją między zmiennymi Xi oraz Xk o zapisujemy
![]()
![]()
Załóżmy, że istnieją ![]()
dla 1≤i, k≤n i ponadto przyjmujemy ![]()
wtedy: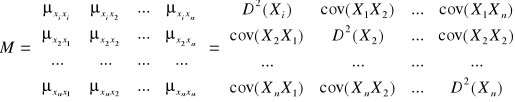
UWAGA !!
Macierz kwadratowa jest symetryczna ![]()
Wyznacznik macierzy M jest ≥0 (det m ≥0)
Szczególny przypadek dla dwuwymiarowej zmiennej losowej (X,Y)
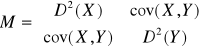
Tw.
Jeżeli zmienne losowe (X,Y) są niezależne i istnieje E(X,Y) (wartośc oczekiwana) to ![]()
Uwaga: ![]()
![]()
(związek momentu centralnego z momentem zwykłym )
Współczynnik korelacji
Niech (X,Y) jest dwuwymiarową zmienną losową .Załóżmy ,że istnieją momenty rzędu 1 i 2
![]()
![]()
![]()
![]()
![]()
Def.
Współczynnikiem korelacji ![]()
między zmiennymi (x, y) nazywamy wyrażenie określone następująco
![]()
przy założeniu ![]()