ZMIENNA LOSOWA
Dane jest doświadczenie określone zbiorem zdarzeń elementarnych E.
Jeśli każdemu zdarzeniu elementarnemu przyporządkujemy liczbę rzeczywistą to mówimy, że została określona zmienna losowa jednowymiarowa - słowo jednowymiarowa zwykle się opuszcza;
Zmienna losowa jest funkcją, której dziedziną jest zbiór zdarzeń elementarnych E, a wartościami liczby rzeczywiste;
Zmienne losowe oznaczamy dużymi literami alfabetu łacińskiego X, Y, …;
Wartości jakie przyjmuje zmienna losowa oznaczamy małymi literami, x, y, …;
Symbol X=x oznacza zdarzenie losowe będące zbiorem tych zdarzeń elementarnych, którym została przyporządkowana liczba x;
Symbol a<X<b oznacza zdarzenie będące zbiorem tych zdarzeń losowych elementarnych, którym przyporządkowano liczby większe od a i mniejsze od b;
Prawdopodobieństwa tych zdarzeń zapisujemy odpowiednio: P(X=x); P(a<X<b).
ZMIENNE LOSOWE SKOKOWE
Zmienna losową, której zbiór wartości jest skończony lub przeliczalny (tzn. taki, że wszystkie jego elementy można ponumerować), nazywamy zmienną losową skokową.
PRZYKŁAD:
Doświadczenie polega na dwukrotnym rzucie kostką do gry. Każdemu z 36 możliwych wyników doświadczenia (zdarzeń elementarnych) przyporządkujemy liczbę równą sumie oczek uzyskanych w obu rzutach.
***
Dziedziną tak określonej zmiennej losowej są zdarzenia elementarne:
1-1;
1-2;
…………
6-6.
Wartościami liczby:
2;
3;
………..
12.
co ilustruje poniższa tabela:
Wynik II rzutu kostką
Wynik I rzutu kostką |
1 |
2 |
3 |
4 |
5 |
6 |
zdarzenia: 1 wartości:
|
1-1
2 |
1-2
3 |
1-3
4 |
1-4
5 |
1-5
6 |
1-6
7 |
zdarzenia: 2 wartości: |
2-1 3 |
2-2 4 |
2-3 5 |
2-4 6 |
2-5 7 |
2-6 8 |
zdarzenia: 3 wartości: |
3-1
4 |
3-2 5 |
3-3 6 |
3-4 7 |
3-5 8 |
3-6 9 |
zdarzenia: 4 wartości: |
4-1
5 |
4-2
6 |
4-3
7 |
4-4
8 |
4-5
9 |
4-6
10 |
zdarzenia: 5 wartości: |
5-1
6 |
5-2
7 |
5-3
8 |
5-4
9 |
5-5
10 |
5-6
11 |
zdarzenia : 6 wartości: |
6-1
7 |
6-2
8 |
6-3
9 |
6-4
10 |
6-5
11 |
6-6
12 |
****
Zakładamy, ze zmienna losowa X jest zmienną losową skokową o wartościach: x1, x2, …., xn, …..
Prawdopodobieństwo tego, że zmienna losowa X przyjmie wartość xi nazywamy funkcją prawdopodobieństwa zmiennej losowej X, i fakt ten zapisujemy w postaci:
P(X=xi)=pi
Dziedzina funkcji prawdopodobieństwa jest skończonym lub przeliczalnym zbiorem liczb rzeczywistych;
Wartościami funkcji prawdopodobieństwa są liczby rzeczywiste dodatnie;
Zachodzi ponadto:
![]()
- dla dziedziny skończonej;
![]()
- dla dziedziny przeliczalnej.
Zakładając, że wszystkie wyniki doświadczenia (w rozpatrywanym przykładzie) są jednakowo możliwe, tzn. prawdopodobieństwo każdego ze zdarzeń elementarnych jest jednakowe i wynosi
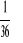
funkcja prawdopodobieństwa zmiennej losowej skokowej jest równa:
P(X=2)=P(1-1)=![]()
P(X=3)=P(1-2)+ P(2-1)=![]()
……………………..
P(X=7)=P(1-6)+P(2-5)+P(3-4)+P(4-3)+P(5-2)+P(6-1)=![]()
……………………………
P(X=12)=P(6-6)= ![]()
Wartości funkcji prawdopodobieństwa przedstawiono w poniższej tabeli:
xi |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
P(X=xi)=pi |
|
|
|
|
|
|
|
|
|
|
|
Przy wyznaczaniu wartości funkcji prawdopodobieństwa wykorzystano tę własność, że prawdopodobieństwo sumy zdarzeń wykluczających się parami jest równe sumie prawdopodobieństw tych zdarzeń;
Poniżej przedstawiono wykres funkcji prawdopodobieństwa zmiennej losowej skokowej:
Obok funkcji prawdopodobieństwa stosuje się jeszcze inną charakterystykę poszczególnych wartości zmiennej losowej.
Funkcję tę oznaczamy F(x) i nazywamy dystrybuantą zmiennej losowej X.
Dystrybuantą zmiennej losowej X nazywamy funkcję określoną wzorem:
F(x)=P(X<x)
Dystrybuanta F(x) zmiennej losowej X o funkcji prawdopodobieństwa P(X=xi)=pi
(tzn. zmiennej losowej skokowej) wyraża się wzorem:
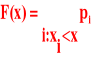
gdzie, sumowanie w powyższym wzorze rozciąga się na wszystkie składniki pi o wskaźnikach i dla których xi<x.
Dystrybuanta skokowej zmiennej losowej X jest funkcją przedziałami stałą i w skończonej lub przeliczalnej liczbie punktów, które są wartościami tej zmiennej ma skoki równe prawdopodobieństwom, z którymi zmienna losowa X te wartości przyjmuje;
Dystrybuanta F(x) zmiennej losowej X ma następujące własności:
F(x) jest funkcją niemalejącą;
F(x) jest funkcją przynajmniej lewostronnie ciągłą:
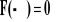
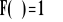

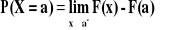
- prawdopodobieństwo , że zmienna losowa X przyjmie wartość a jest równe skokowi dystrybuanty w tym punkcie;Jeżeli a jest punktem ciągłości dystrybuanty F(x), to P(X=a)=0.
Każda funkcja spełniająca warunki 1-4 może być dystrybuantą pewnej zmiennej losowej X.
Dla omówionej w przykładzie zmiennej losowej X jej dystrybuanta F(x)=P(X<x) przyjmuje wartości jak w tabeli poniżej:
Na rysunku poniżej przedstawiono wykres dystrybuanty zmiennej losowej X:
w wielu przypadkach wynikowi doświadczenia przyporządkowana jest dowolna liczbą rzeczywista z określonego przedziału;
stosowanie wówczas modelu dyskretnego nie będzie należytym odzwierciedleniem rzeczywistości - dlatego wprowadza się pojęcie zmiennej losowej ciągłej;
Jeśli zmienna losowa X ma dystrybuantę F(x), która jest funkcją wszędzie ciągłą i jeśli istnieje ciągła pochodna dystrybuanty (z wyjątkiem skończonej liczby punktów), to X nazywamy zmienna losową ciągłą.
Pochodna dystrybuanty F(x) zmiennej losowej ciągłej X jest nazywana funkcją gęstości tej zmiennej losowej i oznaczana przez f(x), tj.
W przypadku, gdy zadana jest funkcja gęstości zmiennej losowej, to dystrybuanta tej zmiennej losowej wyznaczana jest ze wzoru:
Z własności dystrybuanty wynika, że dla punktu ciągłości dystrybuanty prawdopodobieństwo przyjęcia przez zmienną losową tej wartości jest równe zero, wnosimy, że ciągła zmienna losowa przyjmuje każdą pojedynczą wartość z prawdopodobieństwem równym zeru (co nie oznacza, że zdarzenie jest niemożliwe).
Prawdopodobieństwo, że ciągła zmienna losowa przyjmuje wartości z przedziału a, b jest równe:
Funkcja gęstości ma następujące własności:
jest funkcja nieujemną, tj.:
jest funkcją ciągłą (z wyjątkiem co najwyżej skończonej liczby punktów);
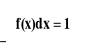
Każda funkcja, która spełnia warunki 1÷3 może być funkcja gęstości pewnej zmiennej losowej.
Z warunku, mamy:
A zatem
na rysunku poniżej przedstawiono wykres funkcji gęstości:
dystrybuantę zmiennej losowej X;
prawdopodobieństwo przyjęcia przez zmienną losową X wartości z przedziału (1/2, 1);
prawdopodobieństwo przyjęcia przez zmienną losową X wartości większej od 1;
Wiemy, że: F(x)=
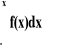
x

0, mamy: F(x)=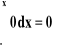
;0 < x < 2, mamy: F(x)=
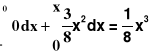
;x

2, mamy: F(x)=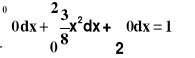
;wykres dystrybuanty przedstawiono poniżej:
Co to jest zmienna losowa
Co to jest zmienna losowa skokowa
Co to jest funkcja prawdopodobieństwa zmiennej losowej skokowej
Co to jest dystrybuanta zmiennej losowej
Jakim wzorem wyraża się dystrybuanta zmiennej losowej skokowej
Podać własności dystrybuanty
Co to jest zmienna losowa ciągła
Co to jest funkcja gęstości zmiennej losowej ciągłej
Podać własności funkcji gęstości
Jakim wzorem wyraża się dystrybuanta zmiennej losowej ciągłej, gdy dana funkcja gęstości
Zmienna losowa przyjmuje wartości: x1=-1; x2=1; x3=4 odpowiednio z prawdopodobieństwami: p1=2/7; p2=4/7; p3=a.
Zorganizowano grę. Rzucamy dwukrotnie kostką do gry. Jeśli suma oczek jest równa 2 otrzymujemy 10 zł; jeśli 3 - 5 zł, a w pozostałych przypadkach płacimy 1 zł.
Zmienna losowa jest całkowicie określona, jeśli znana jest funkcja prawdopodobieństwa w przypadku zmiennej losowej skokowej lub funkcja gęstości w przypadku zmiennej losowej ciągłej;
Zmienna losowa jest całkowicie określona również, jeśli znana jest dystrybuanta zmiennej losowej;
W wielu przypadkach , szczególnie dla celów porównawczych, wygodnie jest charakteryzować rozkład zmiennej losowej przy pomocy wartości pewnych wskaźników, zwanych parametrami rozkładu;
Charakterystyka rozkładu przez wartości parametrów zawiera mniej informacji o rozkładzie niż znajomość funkcji prawdopodobieństwa (lub gęstości) lub dystrybuanty;
Wartością oczekiwaną zmiennej losowej skokowej X przyjmującej skończoną liczbę wartości x1, x2, x3, …, xn odpowiednio z prawdopodobieństwami p1, p2, p3, …, pn nazywamy liczbę określoną jak poniżej:
Wartością oczekiwaną ciągłej zmiennej losowej X o funkcji gęstości f(x) nazywamy liczbę określoną jak poniżej:
wartość oczekiwana stałej jest równa stałej, tj. Eb=b; (b-stała)
stałą można wyłączyć przed znak wartości oczekiwanej: E(aX)=a EX;
E(aX + b) = a E X + b
wartość oczekiwana sumy (różnicy) zmiennych losowych jest równa sumie (różnicy) ich wartości oczekiwanych:
wartość oczekiwana iloczynu zmiennych losowych niezależnych jest równa iloczynowi ich wartości oczekiwanych:
Momentem k-tego rzędu zmiennej losowej X nazywamy wartość oczekiwaną zmiennej losowej Xk i oznaczamy symbolem mk, tj.
Moment k-tego rzędu zmiennej losowej X wyraża się wzorem:
mk =
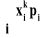
- gdy zmienna losowa X ma rozkład skokowy o funkcji prawdopodobieństwa P(X=xi)=pi;mk =
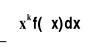
- gdy zmienna losowa X ma rozkład ciągły o funkcji gęstości f(x);Momentem centralnym k-tego rzędu zmiennej losowej X nazywamy wartość oczekiwaną zmiennej losowej (X - m)k , gdzie m - jest wartością oczekiwaną zmiennej losowej X i oznaczamy symbolem

k, tj.Moment centralny k-tego rzędu zmiennej losowej X wyraża się wzorem:

k =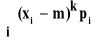
- gdy zmienna losowa X ma rozkład skokowy o funkcji prawdopodobieństwa P(X=xi)=pi;
k =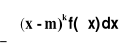
- gdy zmienna losowa X ma rozkład ciągły o funkcji gęstości f(x);Warunkiem istnienia k-tego momentu zwykłego lub centralnego jest bezwzględna zbieżność odpowiedniego szeregu lub całki podobnie jak przy określaniu wartości oczekiwanej.
Szczególne przypadki:
m2 =
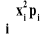
=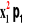
+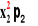
+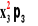
+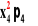
=m3 =
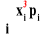
=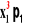
+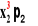
+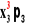
+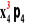
=Ze wzoru wynika, że, aby z niego skorzystać należy wyznaczyć m wartość oczekiwaną. Wiemy, że m=m1, a zatem:
W takim razie moment centralny k-tego rzędu:
Natomiast

2 wyraża się wzorem:Moment pierwszego rzędu zmiennej losowej ciągłej wyraża się wzorem:
Moment drugiego rzędu zmiennej losowej ciągłej wyraża się wzorem:
Moment centralny pierwszego rzędu zmiennej losowej ciągłej wyraża się wzorem:
Moment centralny drugiego rzędu zmiennej losowej ciągłej wyraża się wzorem:
Powtarzające się i niezależne próby nazywamy próbami Bernoulliego, jeżeli każda próba ma tylko dwa możliwe wyniki i ich prawdopodobieństwa pozostają te same przez cały czas prób.
Oznaczamy te prawdopodobieństwa przez p i q. Wyniki o prawdopodobieństwie p nazywamy sukcesem S, a drugi wynik - porażką oznaczamy przez P.
Oczywiście liczby p i q muszą być nieujemne oraz
Przestrzeń wyników każdego indywidualnego doświadczenia składa się z dwóch punktów S i P.
Przestrzeń wyników n doświadczeń Bernoulliego zawiera 2n punktów odpowiadającym 2n ciągom o długości n zawierającym symbole S i P, przy czym każdy punkt przedstawia jeden możliwy wynik doświadczenia złożonego.
Ponieważ próby są niezależne, więc prawdopodobieństwo uzyskania konkretnego ciągu jest iloczynem otrzymanym przez podstawienie zamiast symboli S i P odpowiednio p i q; np.:
Często interesuje nas tylko ogólna ilość sukcesów osiągniętych w ciągu n prób Bernoulliego, a nie ich kolejność. Ilość ta może wynosić 0, 1, 2, …, n.
Zdarzenie: „n prób dało w wyniku k sukcesów i n-k porażek” może zajść na tyle rozmaitych sposobów, ile jest sposobów ustawienia k liter S na n miejscach,
zdarzenie to składa się z
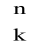
zdarzeń elementarnych.Z poprzedniego wynika, że prawdopodobieństwo zdarzenia elementarnego, zawierającego k sukcesów, jest równe
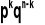
.Zmienna losowa X, której funkcja prawdopodobieństwa wyraża się wzorem
Zmienna losowa X może przyjmować wartości 0, 1, 2, …, 8 równe liczbie uzyskanych 5-tek przy ośmiokrotnym rzucie kostką.
Prawdopodobieństwo sukcesu, tzn. uzyskania 5 oczek w jednym rzucie
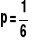
;Prawdopodobieństwo porażki, tzn. uzyskania liczby oczek różnej od 5 w jednym rzucie
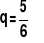
;Interesuje nas zdarzenie uzyskania zera sukcesów w ośmiu niezależnych próbach
Wartości funkcji prawdopodobieństwa zmiennej losowej X podlegającej rozkładowi dwumianowemu dla n=8 przedstawia tabela i rysunek .
Zmienna losowa X podlegająca rozkładowi dwumianowemu ma:
Wartość oczekiwaną
Wariancję
Zmienna losowa X ma rozkład Poissona, jeśli jej funkcja prawdopodobieństwa wyraża się wzorem
Przykładową funkcję prawdopodobieństwa zmiennej losowej X podlegającej rozkładowi Poissona dla
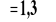
przedstawia poniższy rysunek:Rozkład Poissona ma istotne znaczenie praktyczne z dwóch względów.
Po pierwsze okazało się, że wiele zjawisk fizycznych jak np. rozpad radioaktywny, trafienia Londynu przez bomby latające, błędne połączenia telefoniczne itp. ma rozkład identyczny z rozkładem Poissona.
Po drugie może on w pewnych warunkach stanowić przybliżenie rozkładu dwumianowego, mianowicie jeśli n osiąga duże wartości i p małe, to
Na rys. powyżej przedstawiono wartości funkcji prawdopodobieństwa rozkładu dwumianowego przy
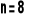
oraz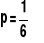
.Dla rozkładu Poissona przy
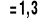
, co jest równe w dużym przybliżeniu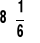
.Zmienna losowa X podlegająca rozkładowi Poissona ma:
Wartość oczekiwaną
Wariancję
Niech zmienna losowa X przyjmuje wartości równe liczbie niedobrych śrub wśród 200 sztuk. Należy obliczyć prawdopodobieństwo zdarzenia X=2. Ponieważ X podlega rozkładowi dwumianowemu o parametrze p=0,015, więc
Wartość tego wyrażenia można obliczyć stosując przybliżenie Poissona dla
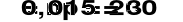
oraz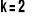
Wśród rozkładów ciągłych najważniejszą rolę, ze względu na szerokie zastosowania, odgrywa rozkład normalny, zwany inaczej rozkład Gaussa.
Zmienna losowa ciągła X podlega rozkładowi normalnemu, jeśli jej funkcja gęstości da się przedstawić w postaci
Dystrybuantę zmiennej losowej o rozkładzie normalnym oznaczamy
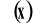
, zatem:Wartość oczekiwaną
Wariancję
Rozkład normalny z wartością oczekiwaną m i odchyleniem standardowym σ oznaczamy
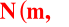
.Rozkład normalny, tzn. jego funkcja gęstości i dystrybuanta dla
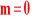
i
są stablicowane.Skorzystamy z właściwości, że jeśli zmienna losowa X ma wartość oczekiwaną m i wariancję σ2, to zmienna losowa Z taka że:
Wpływ odchylenia standardowego na wykres funkcji gęstości rozkładu normalnego ilustruje rysunek poniżej
Widać, że z prawdopodobieństwem praktycznie równym jedności zmienna losowa o rozkładzie normalnym przyjmuje wartości nie różniące się od wartości oczekiwanej więcej niż o 3σ.
Zmienna losowa X ma rozkład wykładniczy, jeśli jej funkcja gęstości wyraża się wzorem
Wartość oczekiwaną
Wariancję
Zmienna losowa ma rozkład równomierny, jeśli jej funkcja gęstości wyraża się wzorem
Wartość oczekiwaną
Wariancję
Jeśli zmienne losowa
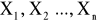
są niezależnymi zmiennymi losowymi i każda z nich podlega rozkładowi normalnemu o wartości oczekiwanej zero i odchyleniu standardowym równemu jeden, to zmienna losowa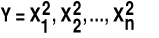
podlega rozkładowi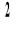
o n stopniach swobody.Rozkład
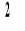
jest stablicowany. W tablicy rozkładu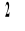
, dla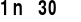
stopni swobody oraz wybranych wartości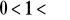
umieszczono liczby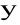
takie, że: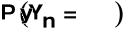
-------------Wartość oczekiwaną
Wariancję
Jakie próby nazywam próbami Bernoulliego?
Jakim wzorem wyraża się prawdopodobieństwo zdarzenia polegającego na wypadnięciu k sukcesów w n doświadczeniach Bernoulliego?
Co to znaczy, że zmienna losowa ma rozkład dwumianowy?
Jaka jest wartość oczekiwana i wariancja zmiennej losowej podlegającej rozkładowi dwumianowemu?
Jakim wzorem wyraża się funkcja prawdopodobieństwa zmiennej losowej o rozkładzie Poissona?
Jaka jest wartość oczekiwana i wariancja zmiennej losowej podlegającej rozkładowi Poissona?
Co to znaczy, że zmienna losowa ma rozkład normalny?
Zmienna losowa X ma rozkład
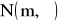
. Jak przekształcić te zmienną, by otrzymać zmienną losową Z o rozkładzie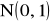
?Jaki wpływ ma wariancja rozkładu normalnego na kształt funkcji gęstości zmiennej losowej?
Ile wynosi prawdopodobieństwo zdarzenia, że zmienna losowa podlegająca rozkładowi normalnemu o wartości oczekiwanej m i wariancji σ2 przyjmie wartości z przedziału (-3σ; 3σ)?
Co to znaczy, że zmienna losowa ma rozkład wykładniczy?
Jaka jest wartość oczekiwana i wariancja zmiennej losowej podlegającej rozkładowi wykładniczemu?
Co to znaczy, że zmienna losowa ma rozkład równomierny?
Jak jest wartość oczekiwana i wariancja zmiennej losowej podlegającej rozkładowi równomiernemu?
Co to jest ilość stopni swobody rozkładu
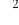
?Jaka jest wartość oczekiwana i wariancja zmiennej losowej podlegającej rozkładowi
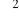
o n stopniach swobody?Co można odczytać z tablic rozkładu
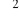
?Jak określamy rozkład t - Studenta o n stopniach swobody?
Co można odczytać z tablic rozkładu t - Studenta?
W hali pracuje 5 maszyn. Prawdopodobieństwo zepsucia się każdej z tych maszyn jest równe
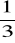
. Maszyny psują się niezależnie od siebie. Obliczyć prawdopodobieństwo, ze:zepsują się 2 maszyny;
zepsuje się 1 maszyna;
nie zepsuje się żadna maszyna;
zepsuje się co najmniej 1 maszyna;
zepsuje się więcej niż 1 maszyna;
zepsuje się co najwyżej 1 maszyna.
Prawdopodobieństwo co najmniej jednego pojawienia się sukcesu przy czterech niezależnych doświadczeniach jest równe 0,59. Jakie jest prawdopodobieństwo pojawienia się sukcesu w jednym doświadczeniu?
Aparatura radiowa składa się z 1000 elementów elektrycznych. Prawdopodobieństwo zepsucia się jednego elementu w ciągu roku pracy jest równe 0,001 i nie zależy od stanu pozostałych elementów. Jakie jest prawdopodobieństwo:
zepsucia się dwóch elementów?
zepsucia się nie mniej niż dwóch elementów?
Wśród ziaren pszenicy znajduje się 0,6% ziaren chwastów. Jakie jest prawdopodobieństwo, że wśród 1000 wybranych losowo ziaren znajdują się:
co najmniej 3 ziarna chwastów?
dokładnie 3 ziarna chwastów?
dokładnie 6 ziaren chwastów?
co najwyżej 3 ziarna chwastów?
![]()
x |
x<2 |
2 |
3 |
4 |
5 |
6 |
7 |
F(x) |
0 |
1/36 |
3/36 |
6/36 |
10/36 |
15/36 |
21/36 |
......
8 |
9 |
10 |
11 |
x |
26/36 |
30/36 |
33/36 |
35/36 |
36/36=1 |
ZMIENNA LOSOWA CIĄGŁA
F'(x)=f(x)
F(x)=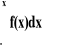
P(a![]()
X![]()
b)= P(a<X![]()
b) - P(a![]()
X<b)=F(b) - F(a)=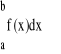
f(x)![]()
o
PRZYKŁAD:
Wyznaczyć stałą c tak, aby funkcja
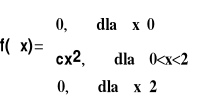
była gęstością pewnej zmiennej losowej X.
****
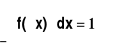
1=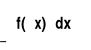
=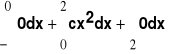
=c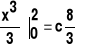
skąd otrzymujemy:
c=![]()
.
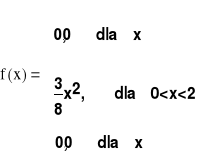
PRZYKŁAD:
Zmienna losowa X ma funkcję gęstości, postaci:
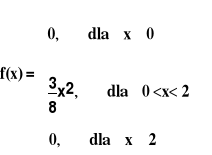
Wyznaczyć:
*****
Ad 1.
Stąd, dla:
Ad 2: P(![]()
<X <1) = F(1) - F(![]()
) = ![]()
- ![]()
= ![]()
Ad 3: P(X> 1) = 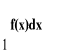
= 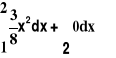
= 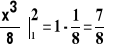
Pytania kontrolne:
Zadania:
Wyznacz a oraz dystrybuantę zmiennej losowej X.
Niech X oznacza wygraną. Znaleźć funkcję prawdopodobieństwa i dystrybuantę zmiennej losowej X.
PARAMETRY ROZKŁADU ZMIENNEJ LOSOWEJ
WARTOŚĆ OCZEKIWANA ZMIENNEJ LOSOWEJ
EX=![]()
przy czym wymagane jest założenie, że szereg
![]()
jest zbieżny.
Jeśli powyższe założenie nie jest spełnione, to zmienna losowa X nie ma wartości oczekiwanej.
EX=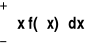
przy czym wymagane jest założenie, że całka
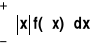
jest zbieżna.
Jeśli powyższe założenie nie jest spełnione, to zmienna losowa X nie ma wartości oczekiwanej.
PRZYKŁAD:
Zmienna losowa X przyjmuje wartości 1, 2, 3, 4, 5, 6 oraz ma funkcję prawdopodobieństwa P(X=xi)=![]()
; i=1, 2, …, 6.
Wyznaczyć wartość oczekiwaną zmiennej losowej X:
EX=![]()
=x1p1 + x2p2 + x3p3 + x4p4 + x5p5 + x6p6 =
= 1![]()
+2![]()
+ 3![]()
+ 4![]()
+ 5![]()
+ 6![]()
= 3,5
PRZYKŁAD:
Zmienna losowa X ciągła ma funkcję gęstości:
f(x)=![]()
Wyznaczyć wartość oczekiwaną zmiennej losowej X:
EX=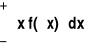
=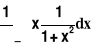
= 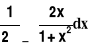
=![]()
Zmienna losowa X nie ma wartości oczekiwanej.
Własności wartości oczekiwanej:
E(X ![]()
Y) = E X ![]()
EY
E(XY) = EX ![]()
EY
Momenty zmiennej losowej
mk = E Xk .
![]()
k = E(X - m)k
m1 = EX = m i to jest wartość oczekiwana zmiennej losowej X;
![]()
1 = E(X-m) = 0;
PRZYKŁAD:
Zmienna losowa X ma funkcję prawdopodobieństwa, jak w tabeli poniżej:
xi |
-2 |
3 |
7 |
11 |
pi |
0.2 |
0.3 |
0.1 |
0.4 |
Wyznacz:
m2, m3
![]()
2, ![]()
3
Wzór na podstawie którego wyznaczamy moment k-tego rzędu ma postać: mk = ![]()
W rozważanym przypadku k=2 oraz 3, przy czym i=1,2,3,4 a więc:
= (-2)2![]()
0.2 + 32![]()
0.3 + 72![]()
0.1 + 112![]()
0.4 =
= 4![]()
0.2 + 9![]()
0.3 + 49![]()
0.1 + 121![]()
0.4 =
= 0.8 + 2.7 + 4.9 + 48.4 = 56.8
= (-2)3![]()
0.2 + 33![]()
0.3 + 73![]()
0.1 + 113![]()
0.4 =
= -8![]()
0.2 + 27![]()
0.3 + 343![]()
0.1 + 1331![]()
0.4 =
= -1.6 + 8.1 + 34.3 +532.4 = 573.2
Wzór na podstawie którego wyznaczamy moment centralny k-tego rzędu ma postać:
![]()
k = ![]()
m1 = ![]()
m =![]()
= ![]()
+ ![]()
+ ![]()
+ ![]()
=
= (-2)![]()
0.2 + 3![]()
0.3 + 7![]()
0.1 + 11![]()
0.4 =
= -0.4 + 0.9 + 0.7 + 4.4 = 5.6
![]()
k = ![]()
przybiera postać: ![]()
k = ![]()
![]()
2 = ![]()
W rozważanym przypadku k=2 oraz 3, przy czym i=1,2,3,4 a więc:
![]()
2 = ![]()
![]()
![]()
= 11.4+2.028+0.196+11.664=25.288
Natomiast ![]()
3 wyraża się wzorem: ![]()
3 = ![]()
tj.:
![]()
3 = ![]()
=![]()
![]()
= -87.552 - 5.2728 + 0.2744 + 62.9856 = -29.5648
PRZYKŁAD:
Zmienna losowa X ma funkcję gęstości:
![]()

Wyznaczyć m1, m2 oraz ![]()
1, ![]()
2.
m1=m=EX=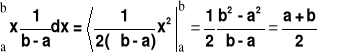
m2=EX2=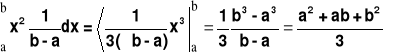
![]()
1=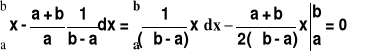
Wiemy, że E(X-m)2= E(X2)-2mEX+m2 = EX2 - m2;
![]()
2=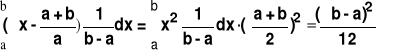
PODSTAWOWE ROZKŁAD PRAWDOPODOBIEŃSTWA
Rozkład dwumianowy
p+q=1
![]()
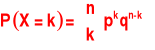
ma rozkład dwumianowy.
Przykład
Rzucamy ośmiokrotnie kostką do gry. Wyznaczyć prawdopodobieństwo zdarzenia polegającego na tym, że w żadnym z rzutów nie pojawi się 5 oczek.
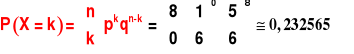
Tabela
X=k |
|
0 |
0,232568 |
1 |
0,372109 |
2 |
0,260476 |
3 |
0,10419 |
4 |
0,026048 |
5 |
0,025038 |
6 |
0,000419 |
7 |
0,0000239 |
8 |
0,000000595 |
Rozkład prawdopodobieństwa zmiennej losowej podlegającej rozkładowi dwumianowemu, dla n=8
![]()
![]()
Rozkład Poissona
![]()
gdzie ![]()
Rozkład prawdopodobieństwa zmiennej losowej podlegającej rozkładowi Poissona dla ![]()
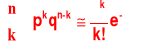
gdzie ![]()
![]()
![]()
Rozkład Poissona jest tablicowany dla różnych wartości parametru ![]()
.
Przykład
Fabryka w M, ma 1,5% braków i nie ma kontroli technicznej. Wyznaczyć prawdopodobieństwo zdarzenia, że w pudełku zawierającym 200 śrub dwie będą niedobre.
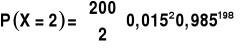
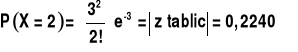
Rozkład normalny
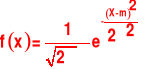
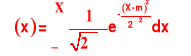
Zmienna losowa X podlegająca rozkładowi normalnemu ma:
![]()
![]()
Przykład
Zmienna losowa X podlega rozkładowi ![]()
, tzn. o wartości oczekiwanej i odchyleniu standardowym 5.
Wyznaczyć prawdopodobieństwo zdarzenia ![]()
.
![]()
ma wartość oczekiwaną zero i wariancję jeden.
Zatem
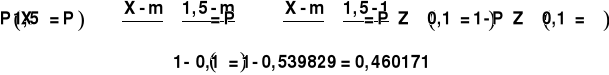
Ponieważ tablice dystrybuanty rozkładu normalnego podane są dla ![]()
, zachodzi potrzeba korzystania z zależności:
![]()
Funkcja gęstości rozkładu normalnego
Dystrybuanta rozkładu N(0, 1)
W oparciu o dane z tablic można stwierdzić, że:

Rozkład wykładniczy
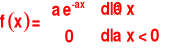
przy ![]()
.
Zmienna losowa X podlegająca rozkładowi wykładniczemu ma:
![]()
![]()
Rysunek przedstawia wykres funkcji gęstości dla rozkładu wykładniczego.
Funkcja gęstości rozkładu wykładniczego
Przykład
Zmienna losowa X podlega rozkładowi wykładniczemu. Wyznaczyć dla jakiej wartości parametru a prawdopodobieństwo zdarzenia, że zmienna losowa X przyjmie wartość mniejszą od jedności, wynosi 0,5
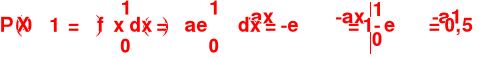
Stąd
![]()
Rozkład Równomierny
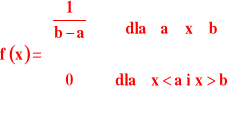
Zmienna losowa X podlegająca rozkładowi równomiernemu ma:
![]()
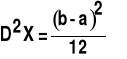
Rysunek poniżej przedstawia wykres funkcji gęstości zmiennej losowej podlegającej rozkładowi równomiernemu:
Funkcja gęstości rozkładu równomiernego
Rozkład χ2 (chi - kwadrat)
co ilustruje rysunek poniżej .
Funkcja gęstości rozkładu f(χ2)
Zmienna losowa X podlegająca rozkładowi ![]()
o n stopniach swobody ma:
![]()
![]()
Jeśli liczba stopni swobody jest większa od 30, to zmienna losowa
![]()
ma w przybliżeniu rozkład normalny o wartości oczekiwanej ![]()
i odchyleniu standardowym ![]()
.
Przykład
Wyznaczyć prawdopodobieństwo, ze zmienna losowa ![]()
, podlegająca rozkładowi ![]()
o siedmiu stopniach swobody, przyjmie wartości z przedziału ![]()
.
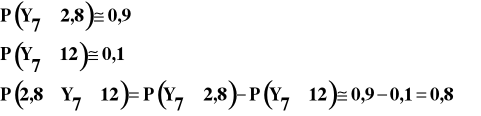
Rozwiązanie ilustruje rozwiązanie przykładu 5
Rezultat jest przybliżony, ponieważ ani dokładnie 2,8 ani dokładnie 12 nie występują w siódmym wierszu tablicy rozkładu![]()
.
Rozkład t- Studenta
Jeśli zmienne losowe X i Yn są zmiennymi losowymi niezależnymi:
X o rozkładzie ![]()
, zaś Yn o rozkładzie ![]()
o n stopniach swobody, to zmienna losowa
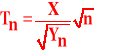
ma rozkład T - Studenta o n stopniach swobody.
Rozkład T - Studenta jest stablicowany. W tablicy rozkładu t - Studenta dla ![]()
stopni swobody i wybranych wartości ![]()
umieszczono liczby ![]()
takie, że: ![]()
Co ilustruje rysunek 9.
Funkcja gęstości rozkładu T - Studenta
Jeśli liczba stopni swobody dąży do nieskończoności, rozkład t - Studenta można przybliżyć rozkładem ![]()
.
PYTANIA KONTROLNE
ZADANIA
15
1/36
6/36
P(X=xi)=pi
xi
2
7
12
1
2
3
12
1/36
7
8
21/36
F(x)
x
1
2
x
f(x)
F(x)
x
1
2
1
X
P(X=k)
0
1
2
3
4
5
6
7
8
0,1
0,2
0,3
0,4
P(X=k)
X
0
1
2
3
4
5
6
7
8
0,1
0,2
0,3
0,4
odpowiednie wartości dla rozkładu dwumianowego n=8, ![]()
1,0
1,5
0,5
X
-3
-2
-1
3
2
1
0
f(x)
σ=0,25
σ=0,50
σ=1,0
0,9986
0,9772
0,8413
1,0
0,5
X
-3
-2
-1
3
2
1
0
1
2
3
4
a=1,0
a=0,1
f(x)
X
0
0,5
1,0
0
m
b
![]()
a
f(x)
X
![]()
yα
f(y)
y
α
y
12
f(y)
y
2,8
![]()
![]()
t
-tα
0
f(t)
tα
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Nowoczesne koncepcje zarzadzania przez jakosc (23-04), WSE notatki, 5 sem
4) EB II Strategia lizbońska, WSE notatki
02 Statystyka Matematyczna Zmienna Losowa Ciągłaid 3789
6 czerwca Zmienna losowa
Zarzadzanie kapitalem intelektualnym organizacji (23-04), WSE notatki, 5 sem
zmienna losowa ciągła, statystyka matematyczna(1)
Wygladzanie wykladnicze (22-58), WSE notatki, 5 sem
3 zmienna losowa odp
36 ?finicja zmiennej losowej Zmienna losowa i jej rozkład
IwZP30 00Y Funkcje i formuły tablicowe, WSE notatki
5. Zmienna losowa, licencjat(1)
zmienna losowa przykład
29 30 Zmienna losowa jednowymiarowa
2 zmienna losowa zadania
zmienna losowa i jej rozklad
Zmienna losowa ciągła wykresy
zmienna losowa, przykład
Zmienna losowa i rozklad prawdopodobienstwa - zadania, Pliki, Studia PK (Mechaniczny & WIL)
więcej podobnych podstron