PODSTAWY FIZYCZNE WYKORZYSTANIA WŁASNOŚCI MAGNETOSPRĘRZYSTYCH DLA OCENY NAPRĘŻEŃ WEWNĘTRZNYCH I ZEWNĘTRZNYCH MATERIAŁÓW FERROMAGNETYCZNYCH

B. Augustyniak

Politechnika Gdańska,

Wydział Fizyki Technicznej i Matematyki Stosowanej

ul. Narutowicza 11/12, 80-952 Gdańsk

1.WSTĘP

Ocena naprężeń w konstrukcjach stalowych jest zagadnieniem o dużym znaczeniu praktycznym. Aplikacja metody rentgenograficznej jest stosunkowo kosztowna i ze względu na koszt aparatur przenośnych a także ze względu na relatywnie długi czas pomiaru dla jednego punktu.

Wskazane jest zatem rozwijanie nowych technik badawczych, które oparte są o specyficzne fizyczne badanych materiałów. Przykładem takich materiałów są stale wykazujące własności ferromagnetyczne. Tego typu materiały są nadal powszechnie używane w przemyśle ciężkim a także w energetyce. W ich przypadku możliwe jest bowiem wykorzystanie ich właściwości magnetosprężystych a w szczególności efektu wpływu naprężeń na strukturę domenową i proces magnesowania.

Celem niniejszego opracowania jest przedstawienie podstaw fizycznych rozwijanych w Wydziale Fizyki Technicznej P.G. nowych metod oceny naprężeń opartych głównie o pomiar określonych parametrów tzw. mechanicznego i magnetycznego efektu Barkhausena. Podane będą podstawowe informacje o własnościach magnetosprężystych ferromagnetyków i o sposobach ich wykorzystania w dziedzinie badań nieniszczących. Przedstawione zostaną również wyniki prac własnych nad wykorzystaniem tych efektów do oceny poziomu naprężeń. Naprężenia te umownie podzielono na wewnętrzne i zewnętrzne. Za naprężenia wewnętrzne przyjęto tutaj uważać naprężenia lokalne występujące w obszarze ziarna materiału polikrystalicznego. Źródłem tych naprężeń są defekty struktury. Naprężenia te modyfikują strukturę magnetyczną ferromagnetyka a tym samym i proces jego magnesowania. Mianem naprężeń zewnętrznych określono naprężenia długozasięgowe, to znaczy występujące w obszarze znacznie większym niż rozmiar ziarna. Takie naprężenia są wytwarzane np. w procesie spawania lub podczas obciążania konstrukcji stalowej..

2. WŁASNOŚCI MAGNETOSPRĘŻYSTE FERROMAGNETYKÓW

2.1. Energia wewnętrzna ferromagnetyków i ich struktura domenowa

Specyficzne własności magnetosprężyste ferromagnetyków wiążą się z występowaniem domen magnetycznych a także z efektem magnetostrykcji, [1,2,3,4]. Domeny magnetyczne mają wymiary rzędu mikrometrów i są to obszary, w których momenty magnetyczne poszczególnych atomów są wzajemnie równoległe. Wielkość domen magnetycznych oraz kierunki ich namagnesowania względem osi krystalograficznych są uwarunkowane poziomem energii wewnętrznej danego obszaru. W warunkach równowagi energia jednostki objętości (gęstość objętościowa energii) przyjmuje wartość minimalną. Energia jednostki objętości ferromagnetyka jest sumą zasadniczo pięciu składników,[4].

Tymi składnikami są: 1) energia wymiany - W_w, 2) energia magnetostatyczna - W_s, 3) energia anizotropii magnetokrystalicznej - W_a, 4) energia magnetosprężysta W_m oraz 6) energia granic domenowych W_d.

Energia wymiany W_w wynika z efektów kwantowych i jest odpowiedzialna za spontaniczne magnesowanie wewnątrz domeny, gdyż jest ona minimalna przy równoległym ustawieniu momentów magnetycznych sąsiednich atomów. Energia ta określa również pośrednio wielkość tzw. energii anizotropii magnetokrystalicznej W_a.

Energia magnetostatyczna W_s związana jest z oddziaływaniem pola magnetycznego na obszar namagnesowany, przy czym uwzględnia się także pole własne magnetyczne wytwarzane przez dany obszar. Pole własne zwiększa energię układu a tym samym przeciwdziała magnesowaniu. Ten efekt opisuje się za pomocą pola demagnetyzującego o natężeniu H_d. Pole to jest proporcjonalne do namagnesowania danego obszaru. Miarą namagnesowania jest wektor J, który wiąże się z bezpośrednio z wektorem magnetyzacji M [A/m] ( M = μ/ V, gdzie μ - moment magnetyczny objętości V) poprzez relację: J = μ_{o ·}M, gdzie μ_o jest przenikalnością magnetyczną próżni. Gęstość energii magnetostatycznej oszacować można stosując zależność:

W_s = -0.5 ·H_d · J - H ⋅ J = - 0.5 · N · J² / μ₀ - H ⋅ J⋅ cos ϕ (1)

gdzie N jest tzw. współczynnikiem rozmagnesowania, zależnym od kształtu obszaru namagnesowanego (0 < N <1) a ϕ - kątem między polem zewnętrznym H i wektorem namagnesowania J. Energia ta jest minimalna, gdy oba wektory są równoległe (ϕ = 0) oraz gdy N jest małe (dla obszarów o wymiarach poprzecznych małych w porównaniu z wymiarem podłużnym, równoległym do kierunku magnesowania).

Energia anizotropii magnetokrystalicznej W_a związana jest z położeniem wektora namagnesowania względem kierunków krystalograficznych. Dla sieci kubicznej gęstość energii wyznacza się według następującego wyrażenia:

W_a = K₁ · [ (α₁ α₂)² + (α₂ α₃)² + (α₁ α₃)²] + K₂ · (α₁α₂α₃)³, (2)

gdzie α_i są dpowiednio kosinusami kierunkowymi dla kątów między wektorem namagnesowania a osiami krystalograficznymi typu <100> a współczynniki K₁ i K₂ są stałymi anizotropii magnetokrystalicznej, charakterystycznymi dla danego materiału. Dla żelaza stałe te wynoszą według [5]: K₁ = 4.5 ·10⁴ a K₂ = 1.5· 10⁴ [J/m³]. Z wyrażenia (2) wynika, że w przypadku żelaza W_a osiąga minimum, gdy wektor namagnesowania jest równoległy do kierunku typu <100>. Kierunek ten jest zatem kierunkiem łatwego magnesowania. Dla niklu stała K₁ jest ujemna i kierunkiem łatwego magnesowania jest zatem kierunek typu <111>.

Energia magnetosprężysta W_m to składnik energii wewnętrznej ferromagnetyka - bardzo ważny dla opisu własności magnetosprężystych. Składnik ten powstaje w naprężonym ferromagnetyku na skutek magnetostrykcyjnego odkształcenia. Efekt magnetostrykcji polega na tym, że odległości między atomami ferromagnetyka ulegają modyfikacji zależnie od kierunku spontanicznego namagnesowania J_s względem osi krystalograficznych.

I tak atomy żelaza magnesowane w kierunku łatwego magnesowania <100> oddalają się od siebie o względną wartość λ₁₀₀ = 20.7 ·10^-6 a magnesowane w kierunku <111> zbliżają o wartość λ₁₁₁ = -21.2 ·10^-6, [6]. Dwie stałe magnetostrykcji: λ₁₀₀ oraz λ₁₁₁ służą do wyznaczania gęstości energii magnetosprężystej ferromagnetyka W_m.

W przypadku działania na ferromagnetyk o strukturze kubicznej jednorodnego naprężenia gęstość energii magnetosprężystej może być wyliczona z wyrażenia:

W_m = -1.5 λ₁₀₀ σ [ (α₁γ₁)² + (α₂γ₂)² + (α₃γ₃)²] -

- 3 λ₁₁₁ σ (α₁α₂γ₁γ₂ + α₂α₃γ₂γ₃ +α₁α₃γ₁γ₃ ), (3)

gdzie odpowiednio: α_i i γ_i są kosinusami kierunkowymi wektora lokalnego namagnesowania J_s oraz naprężenia σ względem kierunków krystalograficznych.

W rachunkach szacunkowych, wystarczajacych dla jakościowej analizy efektów magnetosprężystych, wygodne jest posługiwanie się wyrażeniem zmodyfikowanym, słusznym dla materiałów o magnetostrykcji izotropowej (λ₁₀₀ = λ₁₁₁ = λ_s):

W_m = - 1.5 · λ_s · σ · cos² (ϕ), (4)

gdzie ϕ jest kątem między kierunkiem działania naprężenia σ a kierunkiem wektora namagnesowania lokalnego J_s. Z tego wyrażenia wynika, iż W_m osiaga minimum zależnie od znaku iloczynu λ i σ oraz od wartości kąta ϕ. Minimum tej energii wystąpi dla ϕ = 0, jeśli iloczyn λ_sσ jest dodatni i dla ϕ = 90^o, jeśli iloczyn λ_sσ jest ujemny. W przypadku żelaza przyjmuje się, że stała magnetostrykcji jest dodatnia.

Energia granicy domenowej W_d zależy od typu granicy. Typ granicy określony jest względnymi kierunkami namagnesowania sąsiednich domen. W przypadku materiałów o dodatniej stałej anizotropii K₁ ( a więc i żelaza) obserwuje się dwa typy granic: granice tzw. "90^o" oraz "180^o" stopniowe. Wektory namagnesowania J_s w sąsiednich domenach są albo prostopadłe, albo antyrównoległe. Dla materiałów ze stałą anizotropii K₁ ujemną (np. nikiel), cechujących się kierunkiem łatwego magnesowania typu <111>, występują granice typu 180^o oraz dwa typy granic "nie-180^o" o kątach między kierunkami namagnesowania sąsiednich obszarów odpowiednio 71^o i 109^o. Gęstość energii powierzchniowej granicy domenowej zależy głównie od stałej wymiany A oraz od stałej anizotropii magnetokrystalicznej K₁ a także od typu granicy. Dla żelaza granice domen mają gęstości energii powierzchniowej rzędu 1 J/m² a ich szerokości są zawarte w przedziale od 400 Å dla granic typu "90^o" do 1500 Å dla granic typu "180^o", [7].

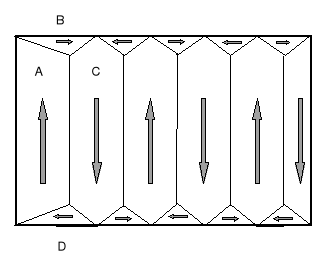
2.2. Struktura domenowa

Rys. 1. Schemat struktury domenowej

Stabilna struktura domenowa odpowiada minimum sumy składników wymienionych wyżej. Na rys. 1 przedstawiono schemat takiej struktury dla monokryształu żelaza wyciętego w kierunku równoległym do [100]. Domeny namagnesowane są głównie w kierunku [100] i są rozdzielone granicami typu "180^o" (domeny A i C, rys. 1). Obniżenie energii układu zapewniają domeny domykające (oznaczone jako B i D). Domeny te są rozdzielone od domen A i C granicami typu "90^o". Pomiędzy obszarami, które są rozdzielone granicami "nie-180^o" występują naprężenia wewnętrzne spowodowanych odmiennymi odkształceniami magnetostrykcyjnymi w tych obszarach. Takich naprężeń nie ma między domenami A i C, albowiem te domeny są odkształcone w ten sam sposób w kierunku w którym leży rozdzielająca je granica "180^o". Przedstawiony na rys. 1 schemat budowy domenowej nie uwzględnia istnienia defektów struktury, które modyfikują istotnie strukturę domenową. Np. granice ziarn oraz wydzielenia faz twardych magnetycznie są miejscem nukleacji nowych domen domykających. Zmienia się ilość domen a tym samym i ilość oraz typ granic domenowych. Takie uproszczenie jest zasadne w przypadku przyjętego tu jakościowego opisu własności magnetosprężystych. Dalszy opis tych własności wspomagany będzie zatem modelem struktury złożonej jedynie z 4 domen, które na rys. 1 zaznaczone jako domeny A, B, C i D.

2.3. Wpływ pola magnetycznego na strukturę domenową

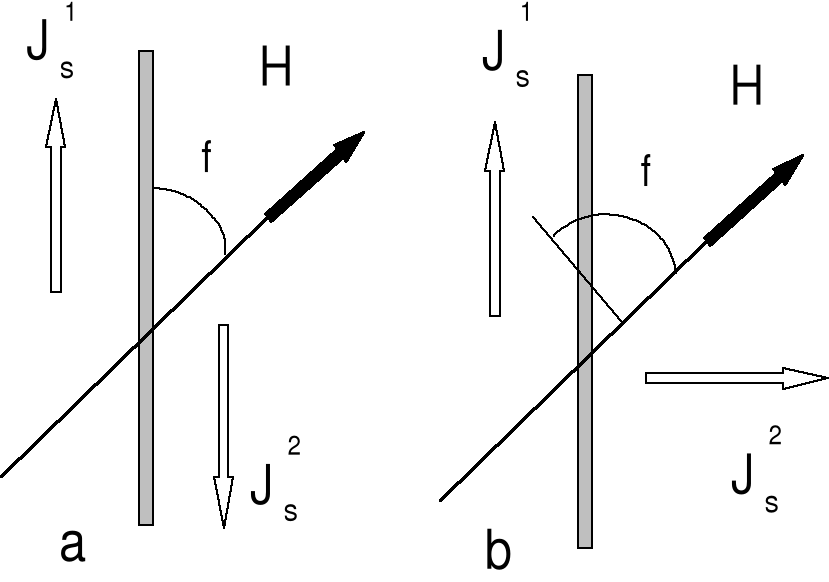
Rys. 2. Przykładowy rozkład przestrzenny pola H oraz namagnesowania J_s dla granicy

"180^o" (a) i "90^o" (b).

Zwiększanie natężenia H zewnętrznego pola magnetycznego powoduje stopniową zmianę struktury domen ferromagnetycznych, która następuje głównie poprzez ruch granic a także poprzez obrót wektorów namagnesowania. Wpływ pola magnetycznego na położenie granicy domenowej określić można za pomocą pojęcia ciśnienia p, które jest bezpośrednio związane z energią magnetostatyczną W_s. Przykładową konfigurację wektorów H oraz J_s przedstawiono na rys. 2 odpowiednio dla granicy "180^o" (rys 2, a) oraz dla granicy "90^o" (rys. 2, b).

Ciśnienie p wywierane na jednostkę powierzchni granicy rozdzielającej dwie domeny namagnesowane wektorami J_s¹ oraz J_s² jest proporcjonalne do natężenia pola H i zależy od wzajemnej konfiguracji namagnesowań i pola magnetycznego. Korzystając z (1):

p = H · (J_s¹ - J_s²) = α· H · J_s · cos(f), (5)

gdzie współczynnik α zależy od typu granicy (α = 2 dla "180^o" i α = √2 dla "90^o") a f jest kątem między H i różnicą obu wektorów J_s, [4]. To ciśnienie powoduje przesunięcie granicy do położenia x, w którym zrównają się wartości ciśnienia p oraz gradientu funkcji W(x):

p = δW(x)/δx, (6)

gdzie x jest położeniem granicy ( kierunek propagacji granicy przyjęto wzdłuż osi x).

Kluczowe znaczenie dla opisu ruchu granicy ma zatem postać funkcji W(x). Za jej pomocą modeluje się lokalne zmiany energii granicy wytworzone przez defekty struktury takie jak wydzielenia faz, granice ziarn, dyslokacje. Zmiany energii W(x) decydują o zakresie odwracalnego ruchu granicy domenowej a także o wielkości skoku Barkhausena. Funkcja W(x) jest specyficzna dla danego typu granicy. Przedstawiony niżej opis ruchu granicy jest ogólny i dotyczy obu typów granic.

.

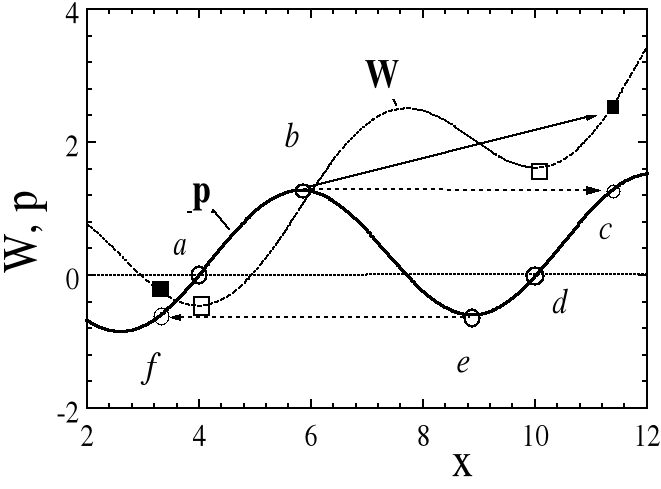
Na rys. 3 pokazano przykładowo wykres funkcji W(x). Funkcję tę utworzono przyjmują najpierw specyficzny przebieg pochodnej δW/δx (funkcja p na rys. 3. Rysunek ten służy do pokazania mechanizmu ruchu granicy a w szczególności skoków Barkhausena.

Rys. 3. Schemat ruchu granicy pod wpływem pola magnetycznego. W(x) - gęstość energii powierzchniowej, p(x) gradient tej energii.

W przypadku braku pola zewnętrznego (H = 0) granica znajduje się w położeniu równowagi, to znaczy - zgodnie z (6), w punkcie a, gdzie W(x) ma wartość lokalnie minimalną a więc δW/δx = 0. Na rys. 3 jest to punkt a o współrzędnych x = 4. Aplikacja pola magnetycznego o natężeniu H powoduje odwracalne przesunięcie granicy w prawo aż do punktu b. W przypadku, gdy ciśnienie od pola H przekroczy poziom ekstremalny p = (δW(x)/δx)_max w punkcie b - następuje skok Barkhausena do punktu c, w którym ciśnienie to zrównoważone jest ponownie z gradientem energii W(x). Dalszy wzrost natężenia pola powoduje dalszy ruch granicy w prawo a zmniejszenie natężenia H - przesunięcie granicy do punktu d, w którym W przyjmuje ponownie lokalnie wartość minimalną. Pod wpływem pola o natężeniu przeciwnym (H<0), granica przemieści się do punktu e, po czym, jeśli ujemne H nadal wzrośnie, granica wykona drugi skok Barkhausena do punktu f. Zredukowanie natężenia pola do poziomu H=0 powoduje powrót granicy do punktu a. W przypadku magnesowania układu złożonego z wielu domen obserwuje się sumę wielu tego typu procesów.

Schemat zmian w strukturze 4 domen dla żelaza wywołany stopniowym wzrostem natężenia pola magnetycznego H pokazano na rys. 4

.

Rys. 4. Schemat wpływu pola magnetycznego

na strukturę domenową

W stanie rozmagnesowanym (rys. 4, A) wypadkowe namagnesowanie całego układu jest minimalne. Umownie przyjęty kierunek <110> działania zewnętrznego pola zaznaczono strzałkami. Dla małych natężeń pola H (H ≈ 10 A/m) występuje ruch odwracalny granic głównie typu "180^o" (rys. 4, B) a następnie nieodwracalny. Dla dużych natężeń H (H rzędu 10⁴ A/m) następują obroty wektorów namagnesowania w kierunku działania pola H. Przy cyklicznych zmianach natężenia pola H powstaje charakterystyczna pętla histerezy między natężeniem pola indukcji magnetycznej B w materiale a natężeniem zewnętrznego pola magnetycznego H. Z pętli tej odczytać można wartość makroskopowego parametru H_c - tzw. pola koercji, dla którego wektor indukcji B magnetycznej wewnątrz materiału jest B = 0. Pole koercji H_c wiąże się pośrednio z rozkładem wysokości lokalnych maksimów gradientu δW/dx , który schematycznie pokazano na rys. 4. Zgodnie z wyrażeniem (5) :

H_c ≈ < (δW/δx)_max /α J_s cos(f)>, (7)

gdzie symbol < > oznacza wartość średnią.

Stworzono wiele modeli, na których podstawie wyznaczano, dla danego typu defektów struktury, relację między H_c a poziomem naprężeń wewnętrznych σ_i wytwarzanych przez te defekty. Naprężenia te można bowiem powiązać bezpośrednio z wartością wysokością barier. Przyjmując za miarę naprężeń wewnętrznych parametr σ_i, który jest średnią wartością z wysokości tych barier, otrzymane określone relacje na H _c, które mają zazwyczaj postać typu [3]:

H_c ≈ β σ_i / J_s, (8)

gdzie współczynnik β jest specyficzny dla przyjętego modelu. Wyrażenie to wskazuje na fakt, iż pole koercji jest tym większe, im większe są naprężenia wewnętrzne wyrażone za pomocą jednego parametru mikrostrukturoskopowego - σ_i.

2.4. Wpływ naprężeń na strukturę domenową

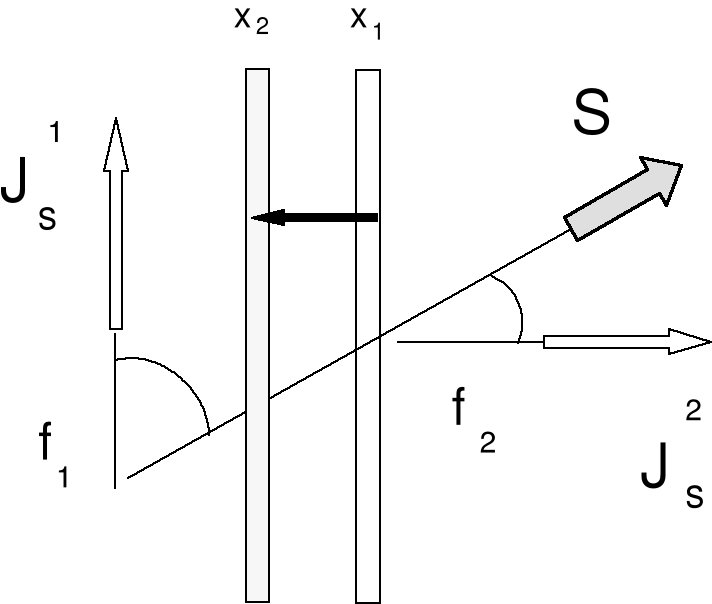
Wpływ naprężeń na położenie granicy domenowej zależy istotnie od typu granicy. Na rys. 5 pokazano schemat ruchu granicy typu "90^o" wymuszonego działaniem jednorodnego naprężenia S. Kąty pomiędzy kierunkiem działania naprężenia a wektorami lokalnego namagnesowania J_sⁱ wynoszą odpowiednio f_i. Na podstawie (4) wnioskować można, iż naprężenie o wartości σ wywoła zmianę energii jednostki objętości o wielkość ΔW_m:

ΔW_m = -1.5·λ_s·σ·[cos²(f₁) - cos²(f₂)] (9)

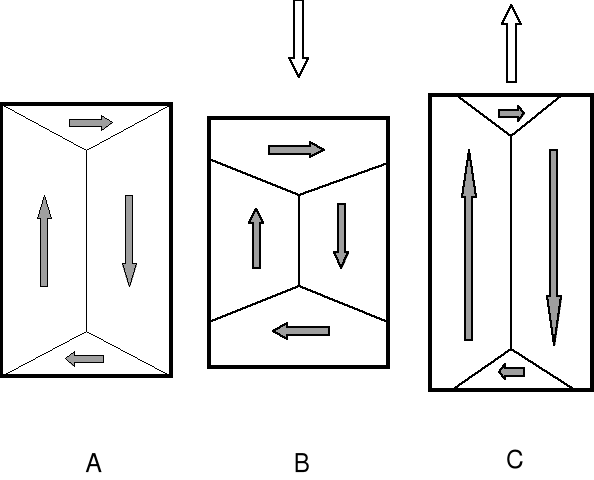
Rys. 5. Rozkład wektorów namagnesowania i naprężenia dla granicy `90^o”

Granica "90^o" przesunie się zatem z punktu x₁ do x₂ w kierunku takim, aby wzrosła objętość domeny prawej z J_s². Na podstawie tego wyrażenia wywnioskować można, iż naprężenie zewnętrzne σ nie zmienia energii domen oddzielonych granicą typu "180^o", ponieważ - ze względu na parzystość funkcji cos²(f), ΔW_m zeruje się dla tego typu granicy. Jest to ważna różnica w skutkach działania pola magnetycznego i naprężeń na strukturę domenową: naprężenia mogą zmieniać położenia jedynie granic "nie-180^o". W przypadku granic typu "180^o" zaaplikowane naprężenie powoduje zmianę szerokości granicy, [4]. Wpływ naprężeń zewnętrznych można porównać formalnie z działaniem równoważnego pola magnetycznego o natężeniu H_σ. Natężenie pola H_σ wynika bowiem wprost z porównania energii magneto-sprężystej i magnetostatycznej :

H_σ ≈ 1.5 λ_s σ / J_s (10)

Rys. 6. Wpływ naprężeń na strukturę domenową

Zmianę struktury domenowej pod wpływem naprężenia dodatniego oraz ujemnego ilustruje schematycznie rys. 6. Pokazano na nim, iż aplikacja naprężeń ujemnych (rys. 3, B) przesuwa granice tak, iż wzrasta objętość domen z J_s prostopadłym do kierunku prostopadłym do kierunku σ.

Naprężenia rozciągające powodują natomiast wzrost domen namagnesowanych wzdłuż kierunku działania σ, (rys. 6, C). Na podkreślenie zasługuje efekt symetrii zmian namagnesowania , który jest przyczyną tego, iż - w pierwszym przybliżeniu, naprężenia nie zmieniają globalnego namagnesowania układu domen. Ruch granic "nie-180^o" wywołany naprężeniem ma również charakter początkowo odwracalny a następnie nieodwracalny. Przy jego opisie ma więc zastosowanie ten sam model rozkładu lokalnych barier, jaki pokazano na rys. 3. Skokowy ruch granic "nie-180^o" jest także źródłem impulsów Barkhausena. Wynika stąd, że skoki Barkhausena występują także podczas naprężania próbki.

Ten typ efektu Barkhausena oznaczać należy jako mechaniczny efekt Barkhausena (MBN) - w celu jego odróżnienia do klasycznego - polowego efektu Barkhausena (HBN). Należy tu podkreślić, że efekt polowy tworzony jest przez obie populacje granic, głównie przez "180^o" a efekt mechaniczny - głównie przez granice "nie-180^o". Ze względu na procentowo znacznie mniejszą ilość i powierzchnię granic "nie-180^o" niż granic typu "180^o", efekt mechaniczny jest wielokrotnie słabszy od klasycznego efektu mechanicznego,[8]

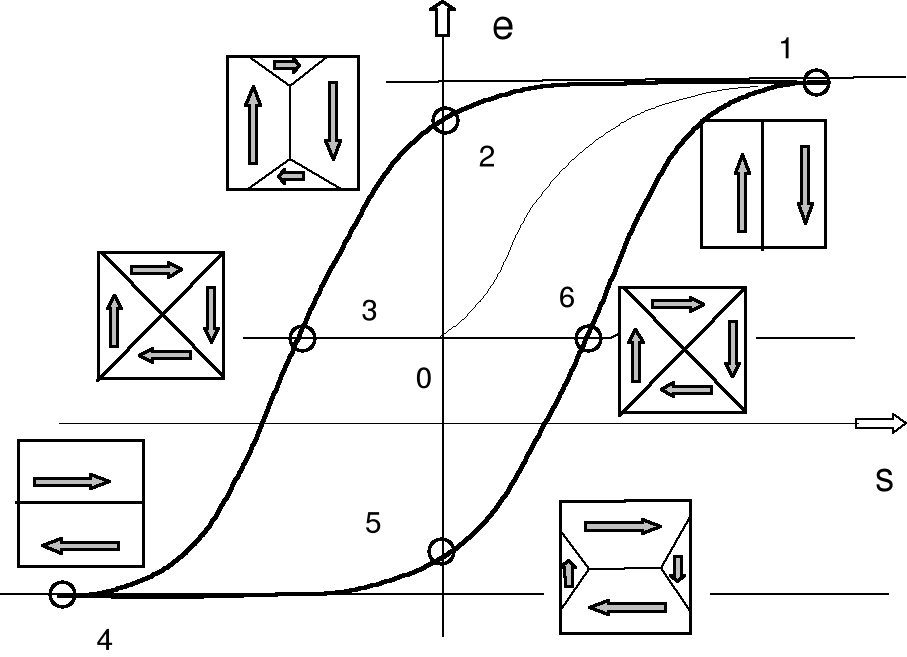
Nałożenie naprężeń zewnętrznych powoduje powstanie dodatkowego odkształcenia o naturze magnetostrykcyjnej ε_λ, które powiększa odkształcenie sprężyste ε_σ. Wielkość odkształcenia magnetosprężystego nie może przekraczać poziomu stałej magnetostrykcji w kierunku łatwego magnesowania. Dla żelaza jest to poziom określony przez stałą λ₁₀₀. W przypadku działania naprężeń przemiennych powstaje pętla histerezy magnetosprężystej ε_λ(σ), która jest analogiem pętli histerezy magnetycznej B(H).

Rys.7. Pętla histerezy magnetosprężystej

Na rys. 7 przed-stawiono schematycznie tego typu pętlę wykorzystując model 4 domen. Na rysunku tym odkształcenie ε_λ oznaczono literą "e" a naprężenie σ literą S. Naprężenie działa w kierunku pionowym. W stanie pierwotnym - próbka jest rozmagnesowana, (punkt (0)) i odkształcona o wartość e₀ = 1/4 λ_100. W stanie nasycenia magnetosprężystego - punkt (1) - odkształcenie osiąga poziom e₁ ≈ λ₁₀₀. W przypadku silnego ściśnięcia - punkt (4) - odkształcenie magnetostrykcyjne ma wartość e₄ = -1/4 λ₁₀₀. Względna zmiana odkształcenia między położeniami (1) i (4) wynosi zatem Δe ≈ 3/2 λ₁₀₀. Straty energii na jednostkę objętości od histerezy magneto-sprężystej W_ms są równe powierzchni pętli histerezy magnetosprężystej z rys. 7.

2.4. Wpływ naprężeń zewnętrznych na proces magnesowania

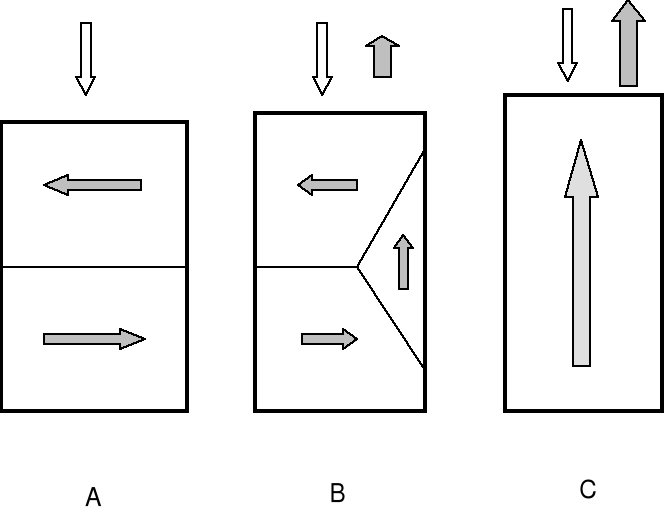
Aplikacja naprężenia zewnętrznego zmienia rozkład populacji domen a tym samym i warunki magnesowania i dzięki temu ten efekt może być wykorzystywany w dziedzinie badań nieniszczących dla oceny naprężeń zewnętrznych lub pozostających. Zmiana struktury domenowej wywołana aplikacją naprężenia a następnie pola magnetycznego pokazana została schematycznie na rysunkach rys. 8 oraz rys. 9, odpowiednio dla naprężeń rozciągających i ściskających.

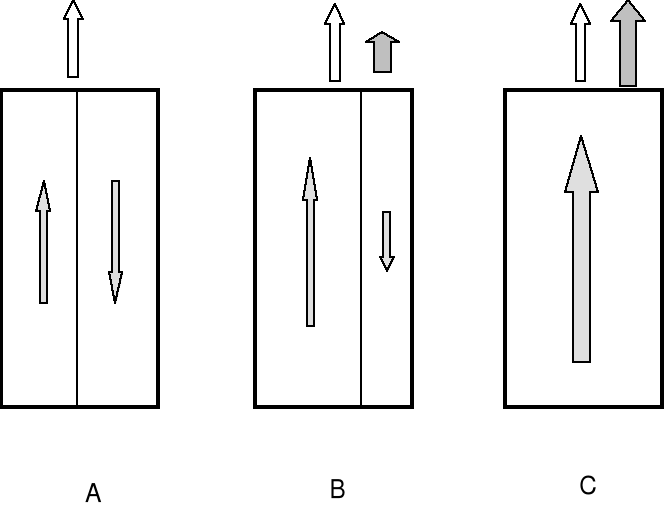
Rys. 8. Magnesowanie próbki poddanej działaniu naprężeń rozciągających.

Rys. 9. Magnesowanie próbki poddanej działaniu naprężeń ściskających.

Rysunki te podkreślają różnice w procesie magnesowania w przypadku stosowania naprężeń rozciągających i ściskających. Przedstawiono przypadek, gdy kierunek magnesowania jest równoległy do kierunku działania naprężeń. W pierwszym przypadku (rys. 8) - zwiększa się ilość domen, których kierunki magnesowania są równoległe do kierunku działania naprężeń rozciągających a tym samym proces magnesowania wynika z ruchu głównie granic typu "180^o" . Naprężenia ściskające (rys. 9) wprowadzają anizotropię rozkładu lokalnego namagnesowania w kierunku prostopadłym do kierunku działania pola H. Tym samym w procesie magnesowania wytwarzane są w znaczącym stopniu granice typu "nie-180^o". Ten etap magnesowania zaznaczono schematycznie na rys. 9 B. Przedstawiony obraz zmian struktury domenowej można uogólnić na układ rzeczywisty wielu domen. Powstała na skutek działania naprężeń anizotropia struktury sprawia, że kierunkiem "łatwego" magnesowania jest kierunek aplikacji naprężeń rozciągających. Kierunek naprężeń ściskających a także kierunek prostopadły do kierunku aplikacji naprężeń rozciągających są natomiast kierunkami "trudnego" magnesowania.

2.5. Relacje ilościowe wpływu naprężeń i pola magnetycznego na strukturę domenową

Za pomocą podanych wyżej wyrażeń, opisujących energię ferromagnetyka można uzyskać praktycznie użyteczne choć szacunkowe oceny dotyczące magnetosprężystych właściwości danego materiału ferromagnetycznego.

Wykorzystać można w tym celu takie wielkości fizyczne jak stałe magnetostrykcji (głównie λ₁₀₀) oraz wektor namagnesowania J_s. Własności sprężyste reprezentowane są przez moduł sztywności Younga E. Dla typowych stali ferrytycznych miękkich magnetycznie użyć można przybliżonych wartości, zachowując - dla uproszczenia rachunków - jedynie rząd ich wielkości. Dla stałej magnetostrykcji przyjąć należy wartość rzędu λ₁₀₀ ∼ 20⋅10^-6, a dla wektora indukcji magnetycznej poziom J_s ∼ 1 T. Dla modułu sztywności można przyjąć wartość E ∼ 200 ⋅ 10³ MPa. Miarą odniesienia może być gęstość energii anizotropii magnetokrystalicznej. Dla żelaza jest to energia rzędu 40 ⋅ kJ/m³. Aby zmienić kierunki wektorów namagnesowania poprzez ich obrót, to znaczy, aby nasycić magnetycznie materiał, należy - zgodnie z (1) i (2) zastosować pole nasycające o natężeniu H ≈ K₁/J_s , a więc o natężeniu H ≈ 40 kA/m.

Bardzo ważnym parametrem mikrostrukuroskopowym jest poziom naprężeń wewnętrznych. Za jego miarę przyjęto wartość średnią lokalnych naprężeń , która podaje się w postacji parametru σ_i. Dolną granicę wartości naprężeń wewnętrznych można oszacować biorąc pod uwagę jedynie naprężenia związane z występowaniem granic "90^o".

Towarzyszące im odkształcenie magnetostrykcyjne na poziomie λ_s wprowadza naprężenia lokalne - zgodnie z prawem Hooke'a - na poziomie σ ≈ λ_s⋅E. Wynika stąd, że te naprężenia wewnętrzne nie są mniejsze niż σ_i ∼ 4 MPa. Poziom naprężeń wewnętrznych powstałych wokół defektów struktury jest na ogół o rząd wielkości większy. Świadczy o tym analiza typowych dla stali wartości pola koercji H_c ∼ 600 A/m. Aby uzyskać szacunkową ocenę wysokości owych barier wykorzystać można wyrażenie (10), które podaje relację między naprężeniem σ a równoważnym mu polem magnetycznym H_σ. W tym wyrażeniu wielkość σ zastąpić można parametrem σ_i i w ten sposób ocenić pole koercji H_c. Z takiej prostej zamiany wynika, że naprężenia wewnętrzne w typowych stalach są poziomie około 40 MPa. Podobny poziom uzyskuje się z ogólnego wyrażenia typu (8), zależnie od przyjętego modelu. Dla przykładu: występujący w tym wyrażeniu współczynnik β przyjmuje w klasycznej teorii magnetyzmu Beckera i Kerstena wartość bliską λ_s, [3].

Analogiczne rozważania prowadzą do oceny wpływu naprężeń zewnętrznych na proces magnesowania. Wykorzystując ponownie wyrażenie (10), można wykazać, że naprężenia zewnętrzne np. na poziomie granicy plastyczności - σ_R ∼ 250 MPa, wywołują zmiany w strukturze domenowej równoważne działaniu pola o natężeniu H ∼ 5 kA/m. Można tę relację odwrócić i twierdzić, iż należy użyć pola o takim właśnie natężeniu, aby oderwać domeny od kotwiczących je defektów, gdy defekty te wytwarzają bariery potencjału na poziomie 250 MPa.

3. PRZYKŁADY WYNIKÓW BADAŃ ORAZ METODY OCENY NAPRĘŻEŃ

Przedstawione rachunki dostarczyły wartości granicznych dla poziomu naprężeń, z jakimi można się w praktyce spotkać w badaniach własności magnetosprężystych. Z jednej strony są to naprężenia lokalne o poziomie minimalnym rzędu kilku MPa a z drugiej - naprężenia dalekiego zasięgu, które mogą przekroczyć granicę plastyczności. Źródłem tych minimalnych naprężeń są, jak pokazano, same granice domenowe. Naprężenia lokalne mogą osiągać poziom znacznie większy. Naprężenia długozasięgowe mogą być wywołane mechanicznym albo termicznym obciążeniem danego elementu konstrukcji. Naprężenia o dużym poziomie powstają np. w wyniku procesu spawania (w strefie wpływu ciepła) albo podczas obróbki mechanicznej (np. szlifowanie).

Opisane wyżej własności magneto-sprężyste stały się podstawą dla opracowania szeregu metod oceny naprężeń. W przypadku oceny naprężeń pozostających podejmowane były prace nad wykorzystaniem w tym celu zmian kształtu pętli histerezy B(H), [9].

Rys.10. Pętle histerezy B(H) stali XC10 dla trzech stanów naprężeń

Na rys. 10 pokazano przykładowo wyniki pomiaru pętli histerezy B(H) otrzymanych dla stali niskowęglowej typu XC10 (0.1% C), poddanej działaniu naprężeń statycznych. Pole magnetyczne było równolegle do kierunku działania naprężeń. Szybkość zmian pola była stała i wynosiła 1.2 kA/m s^-1. Wyniki te dobrze ilustrują charakterystyczne zmiany w kształcie pętli. Obserwuje się zasadniczo dwa efekty wpływu naprężeń: dla naprężeń rozciągających (wykres 1, rys. 10) - obniżenie pola koercji oraz wzrost nachylenia funkcji B(H) w zakresie natężeń bliskich H_c. oraz relacje odwrotną dla naprężeń ściskających (wykres 3, rys.10). Widać więc, że naprężenia rozciągające zwiększają dynamikę procesu histerezowego a naprężenia ściskające - prowadzą do wzrostu twardości magnetycznej.

W przypadku badań w warunkach przemysłowych - uzasadnione zainteresowanie budzi możliwość wykorzystania dla oceny naprężeń dalekiego zasięgu efektu Barkhausena, [10]. Zasadniczą zaletą tego efektu jest łatwa w użyciu zasada detekcji sygnału Barkhausena, oparta o zjawisko indukcji elektromagnetycznej. Lokalne skoki namagnesowania materiału mogą być bowiem rejestrowane za pomocą sondy detekcyjnej zbliżonej do badanej powierzchni. Niezbędne magnesowanie podłoża realizowane jest za pomocą np. elektromagnesu typu U. Z tego względu na tym efekcie skupiona została ostatnio uwaga wielu ośrodków zajmujących się rozwojem nowych technik w dziedzinie badań nieniszczących. Charakterystyczne cechy wpływu naprężeń na natężenie efektu Barkhausena ilustruje rys. 11.

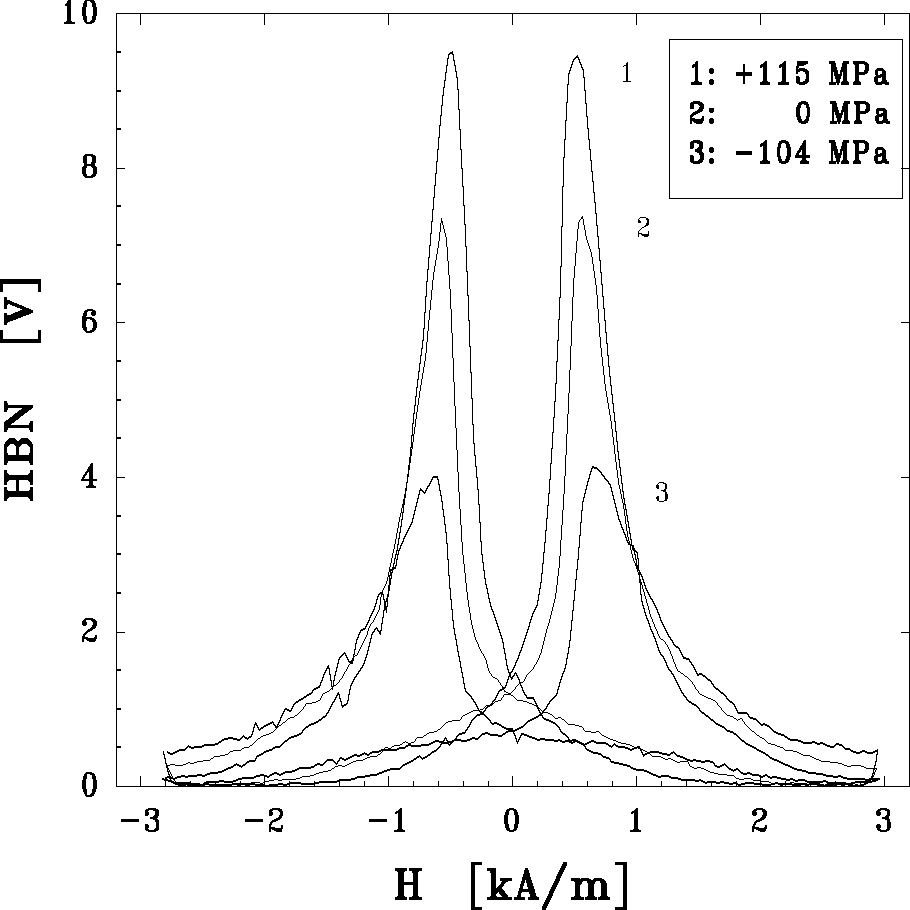
Rys. 11. Wpływ naprężenia na pętle histerezy natężenia efektu Barkhausena stali XC10

Na rys. 11 pokazano wykresy 3 pętli histerezy natężenia efektu Barkhausena, jakie zarejestrowano dla tej samej próbki ze stali XC10, którą poddano działaniu podanych wyżej naprężeń. Można, porównując rys. 10 oraz rys. 11 stwierdzić, iż maksimum natężenia efektu Barkhausena występuje w okolicy natężenia pola koercji H_c. Wysokość tego maksimum i jego położenie zależą silnie od naprężeń w ten sposób, że dla naprężeń dodatnich - (wykres 1, rys. 11) - maksimum to wzrasta i przesuwa się w kierunku słabszych pól a dla naprężeń ujemnych (wykres 3, rys. 11) - maksimum maleje i przesuwa w kierunku silniejszych pól. Można zaobserwować zmianę kształtu wykresu tego maksimum w szczególności w zakresie ujemnych wartości natężenia pola, gdzie następuje nukleacja domen i pierwsze przesunięcia granic powstałych domen. Obserwowany wzrost emisji Barkhausena w tym zakresie zmian pola H dla próbek poddanych naprężeniom ściskającym jest, jak opisano wyżej, spowodowany wzrostem populacji granic typu "nie-180^o". Taki efekt przedstawiono właśnie na rys. 9 B, gdzie zaznaczono powstanie domeny o namagnesowaniu w kierunku działania pola H, ale z granicami typu "90^o".

Przedstawione wyżej wyniki należy traktować jako ilustrację podstawowych efektów związanych z własnościami magnetosprężystymi. Poniżej podane zostaną przykłady wyników prac prowadzonych w Wydziale Fizyki Technicznej Matematyki i Matematyki Stosowanej P.G., mających na celu opracowanie i wdrożenie dwóch istotnie nowych metod oceny poziomu naprężeń z wykorzystaniem efektu Barkhausena. Pierwsza metoda dotyczy oceny funkcji rozkładu naprężeń wewnętrznych na podstawie pomiaru natężenia mechanicznego efektu Barkhausena (MBN), natomiast druga metoda ma na celu określanie naprężeń pozostających w złączach spawanych z wykorzystaniem polowego efektu Barkhausena (HBN).

3.1. Metoda oceny naprężeń wewnętrznych na podstawie mechanicznego efektu Barkhausena MBN

Poziom naprężeń wewnętrznych w fenomenologicznych modelach określany jest za pomocą parametru σ_i. Jest to wartość średnia z lokalnie występujących naprężeń. Kluczowym zagadnieniem dla oceny charakteru naprężeń wewnętrznych w danym materiale ma nie tyle wartość tego parametru ile rozkład gęstości prawdopodobieństwa wystąpienia lokalnie naprężenia o wartości σ_{l .} Rozkład ten dostarcza pełnych informacji o naprężeniach. Na jego podstawie ustalić można np. zakres występujących naprężeń a także naprężenia, które występują z największym prawdopodobieństwem. Podana niżej definicja funkcji rozkładu naprężeń wewnętrznych jest związana ze zjawiskiem histerezy magnetosprężystej .

Ferromagnetyk poddany działaniu naprężeniu σ - ulega, jak to opisano w paragrafie 2.4. lokalnym zmianom struktury domenowej, głównie na skutek ruchu granic "nie-180^o". Jeśli ruch ten jest skokowy - wystąpią w jednostce objętości straty energii ΔW_l związane z propagacją tzw. "mechanicznego" skoku Barkhausena. Warunkiem wystąpienia tych strat jest przekroczenie przez naprężenia zewnętrzne o wartości σ poziomu lokalnych naprężeń σ_l. Według Birczaka i Smitha, gęstość prawdopodobieństwa wystąpienia lokalnych naprężeń na poziomie σ_l opisane jest funkcją N(σ_l), którą wykorzystali dla wyznaczenia prawdopodobieństwa wystąpienia strat energii na histerezę magnetosprężystą, [11,12]. Gdy naprężenie zewnętrzne σ zmieniane jest w przedziale wartości od σ do σ + dσ, to zmiana struktury magnetycznej poprzez ruch nieodwracalny granic domenowych wystąpi w ułamku objętości ΔV/V ferromagnetyka tym większym, im większe jest prawdopodobieństwo tego, iż lokalnie występują naprężenia w przedziale σ < σ_l < σ + dσ:

ΔV(σ) = V · N(σ_l ) · dσ, (11)

gdzie funkcja N(σ_l) jest szukana funkcją gęstości prawdopodobieństwa wystąpienia naprężeń lokalnych. Średnia wartość naprężeń lokalnych σ_i wyliczona może być dla zadanej funkcji N(σ_l) z wyrażenia:

σ_i = ∫ σ_l · N(σ_l) dσ / ∫ N(σ_l) dσ, (12)

gdzie całki wyliczone są granicach od σ = 0 do σ = ∞.

Hrianca , [12] a także Birchak i Smith, opierając się na wynikach badań efektu histerezy magnetosprężystej postulowali przyjęcie funkcji N(σ_l) typu wykładniczego,

N(σ_l) = C · σ_l · exp(-ασ_lⁿ), (13)

gdzie wykładnik n może przyjmować wartości całkowite (n = 1,2,...), a stałe C i α są dobierane tak, aby funkcja N(σ_l) była unormowana, to znaczy, aby granicach od σ = 0 do σ = ∞ całka typu ∫ N(σ) dσ = 1. Dla n = 1 funkcja ta przyjmuje zatem postać:

N(σ_l) = (4 σ_l /σ_i²) · exp(- 2 σ_l / σ_i ), (14)

gdzie σ_i jest parametrem opisującym średni poziom naprężeń wewnętrznych.

Podkreślić tu należy, iż postulowana dotychczas postać funkcji N(σ) uwarunkowana była znanymi z doświadczeń cechami efektu histerezy magnetosprężystej. W przypadku próbki poddanej działaniu naprężeń przemiennych o coraz większej amplitudzie drgań σ_o, obserwuje się charakterystyczne dla danego materiału maksimum tarcia wewnętrznego, które świadczy o nasycaniu się strat energii na histerezę magnetosprężystą.

Straty energii na jednostkę objętości ΔW_h w jednym cyklu drgań mechanicznych o amplitudzie σ_o są całką ze strat lokalnych ΔW_l powstałych na skutek skoków Barkhausena przy naprężaniu materiału

ΔW_h = ∫ ΔW_l · N(σ_l) dσ_l, (15)

gdzie całkowanie jest w granicach od 0 do σ_o, a straty lokalne na histerezę są uzależnione od powierzchni elementarnych pętli histerezy magnetosprężystej. Przykład tej pętli przedstawia rys. (7). Birchak i Smith zaproponowali dla oceny tej powierzchni wyrażenie:

ΔW_l = K·λ · σ_l, (16)

gdzie stała K określa kształt pętli (jest rzędu jedności i nie większa od K ≤ 3) a λ jest stałą magnetostrykcji dla kierunku łatwego magnesowania.

Należy tu podkreślić, iż funkcje N(σ) były wyznaczane na podstawie oceny znanych z pomiarów zależności amplitudowych tarcia wewnętrznego, a więc w sposób pośredni to znaczy na podstawie wartości całek z funkcji N(σ) danych np. wzorem (15), [4]. Funkcje N(σ) dobierane są w tym przypadku arbitralnie, zależnie od wyników doświadczenia. Dla żelaza czystego lepsze dopasowanie do wyników uzyskuje się stosując funkcję N(σ) z n = 2 niż z n = 1, [4]. Dobre jakościowo dopasowanie dla stali niskowęglowych dawała natomiast funkcja z n = 1, [11] . Funkcja tego typu była również dla opisu zależności amplitudowych tarcia wewnętrznego czystego niklu, [13]. Wydaje się zatem zasadne poszukiwane metody, która prowadziłaby do ustalenia funkcji N(σ) w sposób bardziej bezpośredni. Taką metodą, szczególnie predysponowaną do tego celu, jest metoda oparta o pomiar emisji mechanicznego efektu Barkhausena (MBN), [14]. Emisja ta, związana z nieodwracalnymi skokami granic "nie-180^o", jest nowym cennym źródłem informacji o procesie histerezy magnetosprężystej. Przykład pętli histerezy natężenia MBN pokazano na rys. 12.

Rys. 12.Pętle histerezy magnetosprężystej stali XC38

Próbkę stali XC38 poddano działaniu naprężeń przemiennych o stałej prędkości zmian naprężenia dσ/dt ≈ 40 MPa/s. Natężenie emisji Barkhausena określano stosując metodę całkowania sygnału napięciowego indukowanego w cewce nawiniętej na próbce. Na rys. 12 pokazano zmiany natężenia MBN w trakcie rozciągania od stanu σ = 0 do wartości maksymalnej σ_o = 75 MPa i do wartości przeciwnej, tzn. - σ₀ (wykres 1) oraz od -σ_o do +σ_o (wykres 2) i ponownie od +σ_o do -σ_o (wykres 3). Zwraca uwagę stopniowy rozwój pętli histerezy, aż do jej stabilizacji po kilku okresach zmian naprężenia. Maksimum natężenia emisji MBN podczas pierwotnego rozciągania występuje w zakresie naprężeń około 60 MPa.

Inne jest położenie maksimum natężenia MBN dla próbki, która poddana została już działaniu dużych naprężeń: maksimum to występuje w zakresie naprężeń o wartości około 20 MPa. Zmiana położenia maksimum wynika z modyfikacji struktury domenowej próbki uprzednio naprężonej. Rejestrowana wartość natężenia emisji MBN jest proporcjonalna do częstości występowania skoków Barkhausena (a tym samym i liczby impulsów napięcia indukowanego w cewce pomiarowej) oraz do wielkości przemagnesowanego obszaru a więc i wysokości indukowanych impulsów napięciowych). Wystąpienie emisji MBN oznacza, że naprężenie zewnętrzne osiągnęło poziom porównywalny z wysokością lokalnych naprężeń lokalnych, które blokowały ruch granic domenowych. Położenie maksimum MBN dla pierwotnego naprężania wskazuje zatem bezpośrednio na rozkład naprężeń wewnętrznych - zwiększenie emisji występuje bowiem wtedy, gdy większa liczba granic "nie-180^o" wykonuje skoki Barkhausena.

Na tej przesłance oparto opisaną niżej metodę badania funkcji N(σ). Ta metoda wiąże się z potwierdzoną doświadczalnie podstawową cechą emisji MBN a mianowicie występowaniem korelacji między natężeniem emisji MBN a stratami energii. Wyniki szczegółowych badań relacji miedzy natężeniem MBN a stratami energii ΔW_h w jednym cyklu drgań mechanicznych wykazały bowiem, iż dla wielu materiałów występuje proporcjonalność między całką z pętli histerezy natężenia MBN a ΔW_h [15,16,17]. Wobec stwierdzonej doświadczalnie relacji typu:

ΔW_h ≈ ∫ U(σ) dσ, (17)

gdzie U(σ) jest natężeniem MBN, można - na podstawie (16) i (17), przyjąć, iż natężenie MBN jest proporcjonalne do iloczynu działającego naprężenia σ i funkcji rozkładu naprężeń N(σ):

U(σ) = A· σ · N(σ). (18)

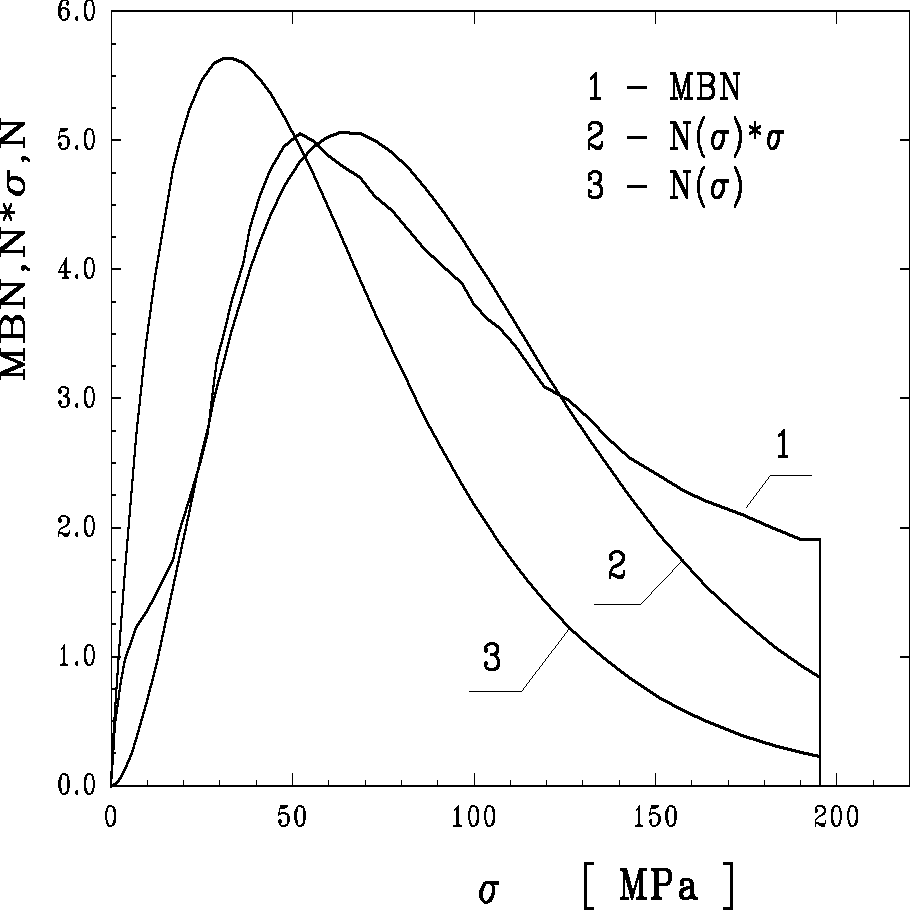
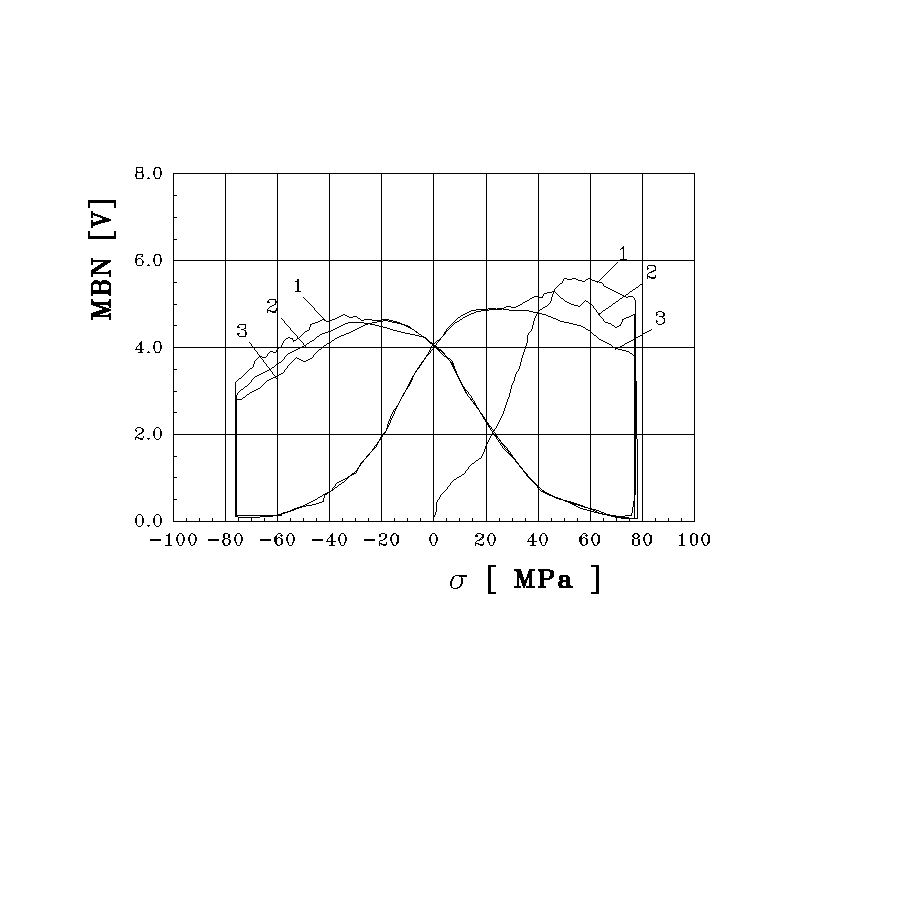
Rys. 13. Wyniki pomiaru natężenia MBN dla stali XC38 -(1) oraz funkcja typu N(σ)·σ - (2) oraz funkcja N(σ) - (3).

Relacja (18) może być zatem podstawą dla wyznaczania funkcji N(σ). Proponowana metoda bazuje jedynie na wynikach pomiaru natężenia MBN podczas pierwszego naprężania próbki. Sposób postępowania zilustrowany zostanie wynikami badań wykonanych dla stali XC38. Na rys. 13 pokazano wynik pomiaru natężenia MBN (wykres 1) w zakresie naprężeń od 0 do 195 MPa. Wyniki te uzupełniają wykres z rys. 12 w zakresie większych naprężeń. Natężenie emisji MBN, po osiągnięciu poziomu maksymalnego dla σ ≈ 60 MPa, maleje lecz nie zanika dla największych naprężeń. Oznacza to, że w tym materiale występują bariery naprężeń lokalnych o poziomie wyższym niż 200 MPa.

Zgodnie z przyjętą relacją (18), funkcję natężenia MBN porównano z wykresem funkcji typu N(σ)·σ. Jako funkcję N(σ) przyjęto funkcję z n = 1, daną wyrażeniem (14). Dopasowanie polegało na doborze parametru σ_i oraz współczynnika A .

Jak widać, dane doświadczalne są w sposób zadawalający opisane przez iloczyn N(σ)·σ a to oznacza, iż przyjęta funkcja N(σ) z wykładnikiem n = 1 może być przyjęta jako funkcja rozkładu naprężeń wewnętrznych dla badanej stali. Przebieg tej funkcji ilustruje wykres 3 na rys. 13. Maksimum gęstości prawdopodobieństwa występuje dla σ ≈ 30 MPa. Wynika stąd, że w nadanym materiale najczęściej występują naprężenia lokalne o takim właśnie poziomie. Natomiast wyliczona wartość średnia naprężeń - czyli parametr σ_i - ma wartość σ_i = 60 ± 5 MPa.

Należy tu zwrócić uwagę, iż maksimum funkcji MBN (wykres 1, rys. 13) występuje w okolicy naprężeń bliskich wartości parametru σ_i. Taka relacja ma duże znaczenie praktyczne, gdyż może być wykorzystana dla szybkiej oceny wartości parametru σ_i.. Podkreślić należy także i to, że przedstawiona na rys. 13 zależność natężenia MBN od przyłożonego naprężenia stanowi istotnie nowe źródło informacji procesie histerezy a w szczególności o rozkładzie naprężeń w badanym materiale. Umożliwia poznanie rozkładu strat energii a tym samym i rozkładu naprężeń wewnętrznych bez konieczności przyjmowania hipotez co do formy funkcji N(σ).

3.2. Metoda oceny naprężeń pozostających na podstawie polowego efektu

Barkhausena HBN

Druga opisana tu metoda dotyczy oceny naprężeń długozasięgowych. Oparta jest o pokazane na rys. 12 ogólnie stwierdzone relacje między charakterem zmian natężenia polowego efektu Barkhausena (HBN) a poziomem przyłożonych do próbki naprężeń σ. Zasadnicze znaczenie dla skuteczności i czułości realizowanej w praktyce przemysłowej metody badań nieniszczących opartej o efekt Barkhausena ma dobór parametru, który jest miarą natężenia efektu Barkhausena. Znane są rozwiązania, które bazują na pomiarze wartości maksymalnej natężenia HBN a także na pomiarze wartości uśrednionej z napięcia impulsów. Na podstawie wyników podanych na rys. 12, można zauważyć, że np. wartość maksymalna natężenia HBN zmienia się blisko dwa razy w przypadku zmian naprężenia w zakresie ± 100 MPa. Po wykonaniu szeregu analiz wybrano dla potrzeb nowo opracowanej metody parametr N, związany z liczbą impulsów Barkhausena, którego pomiar znacznie zwiększa dynamikę zmian sygnału w funkcji przyłożonych naprężeń. Ze względu na brak ilościowego modelu wiążącego natężenie HBN z poziomem naprężeń, zastosowano w nowej metodzie procedurę skalowania relacji między wartością parametru N z poziomem naprężeń σ: N = Z(σ). Korzystając z funkcji będącej transformatą typu σ = Z^-1(N) można odczytać poziom σ na podstawie zmierzonej wartości parametru N. W przypadku badania naprężeń pozostających w złączach spawanych należy uwzględnić fakt występowania rozkładu przestrzennego tych naprężeń. Wymaga to skalowania funkcji Z dla co najmniej dwóch kierunków pomiaru. Bardzo ważnym elementem nowej metody jest przyjęty sposób skalowania. Fakty doświadczalne wskazują na to, że natężenie HBN jest związane nie z poziomem naprężeń działających lokalnie w danym kierunku lecz z poziomem odkształceń w tym kierunku, [18]. Z tego względu skalowanie parametru N odbywa się w dziedzinie odkształceń ε zadawanych w dwóch wzajemnie prostopadłych kierunkach x i y. Pomiary parametru N wykonywane są dwukrotnie: dla kierunku x i dla kierunku y. Tworzone są zatem dwie macierze skalowania Zx(ε_x, ε_y) oraz Zy(ε_x, ε_y) , odpowiednio dla wyników pomiaru w kierunku x i w kierunku y. Dla materiałów izotropowych obie funkcje powinny być identyczne.

W przypadku wystąpienia anizotropii własności magnetosprężystych, będącej wynikiem np. procesu produkcji blach (np. walcowanie wprowadza teksturę), konieczne jest wykorzystanie obu funkcji skalowania. Procedura wyznaczenia poziomu naprężeń pozostających w danym punkcie składa się z kilku etapów. Rozpoczynając pomiar na płycie, należy w danym punkcie znaleźć kierunek osi głównej naprężeń. Jest to kierunek, w którym stwierdza się największe natężenie HBN. Ten kierunek przyjmuje się jako kierunek x.

Pomiary parametru N wykonuje się dla kierunku głównego oraz dla kierunku doń prostopadłego (przyjętego jako kierunek y). Na podstawie tych dwóch wyników - wylicza się z macierzy Zx i Zy najpierw poziomy odkształceń dla tych kierunków: ε_x oraz ε_y a następnie - w oparciu o elementarne przekształcenia z teorii sprężystości - składowe naprężeń σ_x oraz σ_y.:

σ_x = E (ε_x + ν ε_y) / (1 - ν²) (19a)

σ_y = E (ε_y + ν ε_x) / (1 - ν²), (19b)

gdzie E jest modułem sztywności Younga (E = 220 ⋅10³ MPa) a ν jest współczynnikiem Poissona (ν ≈ 0.3). Poziom odkształceń wyznaczany jest metodą interpolacji lub ekstrapolacji z wartości funkcji skalowania Zx i Zy.

Rys. 14. Przestrzenny obraz funkcji skalowania Zx dla stali St3.

Odkształcenia ε mierzono po przeciwnej stronie płyty.

Opisaną procedurę zilustrują wyniki badań naprężeń pozostających w złączach spawanych z blach stali St3 o grubości h = 6 mm. Skalowanie funkcji Z wykonano stosując metodę gięcia. Próbki do skalowania miały kształt krzyża o szerokości ramion 50 mm. Tensometry były naklejone w centrum próbki. Pomiary HBN wykonywano za pomocą sondy dotykowej z rdzeniem magnesującym w kształcie litery U. Bieguny magnesu miały rozwartość około 12 mm. Czujnik emisji Barkhausena rejestrował sygnał emisji HBN z powierzchni około 1 mm². Sonda umieszczona była centralnie po stronie przeciwległej do tensometrów. Sprawdzono, iż zadawane odkształcenia były po obu stronach płyty wzajemnie symetryczne. Odkształcenia mierzono z dokładnością na poziomie ± 1 μdef ( 1 μdef = 1·10^-6). Natężenie HBN oraz parametr N były mierzone za pomocą układu elektronicznego, który umożliwiał detekcję impulsów Barkhausena na poziomie 10 μV w odniesieniu do zacisków cewki pomiarowej.

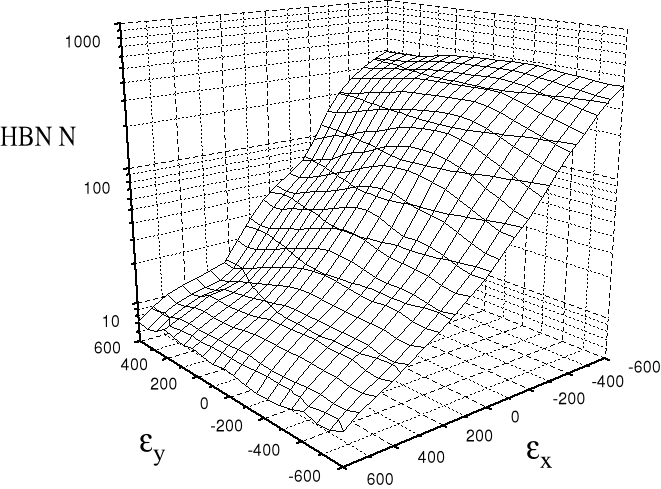
Wykres przestrzenny funkcji skalowania Zx(ε_x, ε_y) dla stali St3 pokazano na rys. 14.

Wartości ε są podane bez korekty znaku: znak ujemny ε oznacza w tym przypadku ściśnięcie od strony przeciwnej - czyli ociągnięcie powierzchni po stronie sondy.. Należy podkreślić bardzo dużą dynamikę zmian wartości parametru N w funkcji zadanych odkształceń ε. Skalowanie wykonano w zakresie ± 600 μdef, co odpowiada naprężeniom na poziomie ±130 MPa.

Jak widać wartość N zmierzona w kierunku x zmienia się blisko 100 razy dla tego zakresu zmian odkształceń ε_x, co stanowi istotny postęp w tej dziedzinie badań i świadczy o bardzo dużej rozdzielczości w ocenie poziomu odkształceń za pomocą opracowanej metody. Dla porównania można tutaj podać, iż dynamika zmian parametru tak zwanego MP w funkcji odkształceń, jaki wykazuje firma A.S.T. z USA produkująca aparaty STRESSCAN, jest znacznie mniejsza, [19].

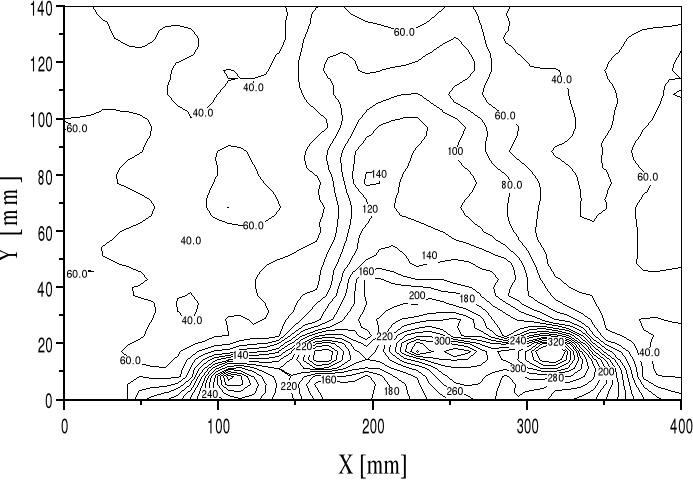
Rys. 15. Mapa izolinii natężenia efektu Barkhausena (parametr N) dla płyty ze stali St3 spawanej doczołowo wzdłuż dolnej krawędzi (pomiędzy 100 i 350 mm). Pomiar wykonano w kierunku równoległym do osi spoiny.

Zmiany poziomu parametru N w funkcji odkształceń w kierunku y (prostopadłym do kierunku działania pola) okazały się nie być monotoniczne dla stali St3. Występuje wyraźne maksimum w zakresie niewielkich odkształceń ε_y Jest to zapewne efekt istnienia w badanym materiale naprężeń pozostających po procesie produkcji. Tego typu niejednoznaczność wartości parametru N nie jest przeszkodą przy wyznaczaniu obu składowych odkształceń, gdyż używa się w tym celu dwóch wyników pomiarów w kierunkach wzajemnie prostopadłych.

Przykład rozkładu sygnału Barkhausena na powierzchni spawanej płyty ze stali St3 pokazano na rys. 15. Płyta o wymiarach 400 mm na 150 mm była spoinowana do drugiej podobnej płyty spoiną doczołową wzdłuż dolnej krawędzi. Spoina zawarta jest pomiędzy punktami o współrzędnych 100 mm i 350 mm. Pokazane wyniki dotyczą pomiarów parametru N w kierunku prostopadłym do spoiny. Pomiary wykonywano w węzłach siatki o wymiarach 5 mm na 15 mm w strefie do 40 mm od spoiny oraz o wymiarach 10 mm na 15 mm w pozostałej części płyty. Zauważyć można znaczne zmiany poziomu parametru N. Jego wartości mieszczą się w przedziale od N = 40 do N = 320. Maksimum natężenia HBN jest wyraźnie oddalone od osi spoiny. Strefa podwyższonego natężenia HBN ma kształt trójkąta o podstawie wzdłuż spoiny i o wierzchołku sięgającym przeciwległego brzegu płyty. Na podstawie tych wyników oraz wyników pomiaru parametru N dla kierunku równoległego do osi spoiny wykonano obliczenia macierzy odkształceń ε_x oraz ε_y w kierunkach odpowiednio wzdłuż i prostopadle do osi spoiny.

Rezultat transformacji tych wyników w macierz składowej σ_y został pokazany na rys. 16. Są to naprężenia działające w kierunku prostopadłym do osi spoiny.

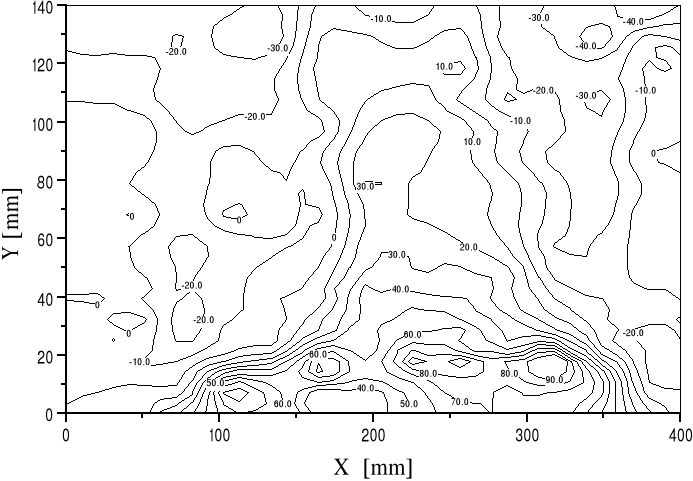
Rys. 16. Izolinie naprężeń w kierunku prostopadłym do osi spoiny dla płyty ze stali St3.

Przedstawiony obraz ujawnia wyraźnie strefy występowania naprężeń ściskających oraz rozciągających. Izolinia σ_y = 0 wydziela strefę środkową płyty, w której naprężenia są dodatnie. Naprężenia ujemne osiągają poziom około -30 MPa w strefach leżących po prawej i lewej stronie płyty. Największe naprężenia rozciągające ( do + 100 MPa) występują w odległości około 20 mm od osi spoiny. Obraz ten jest jakościowo zgodny z danymi literaturowymi o rozkładzie naprężeń pozostających w złączach spawanych. Został on także potwierdzony ilościowo przez wyniki symulacji komputerowej procesu spawania

4. WYKORZYSTANIE WŁASNOŚCI MAGNETOSPRĘŻYSTYCH W DZIEDZINIE BADAŃ NIENISZCZĄCYCH

Aktualny stan badań nad aplikacją własności magnetosprężystych stali ferrytycznych w dziedzinie badań nieniszczących jest na tyle zaawansowany, iż zapewnia opracowanie nowych w kraju i konkurencyjnych wobec np. metody rentgenowskiej metod pomiaru naprężeń przydatnych dla praktyki przemysłowej. Wyniki ostatnio prowadzonych prac nad weryfikacją skuteczności używanych w kraju aparatów rentgenowskich wykazały wyraźnie, że w tej dziedzinie badań należy wykonać istotny krok w kierunku unowocześnienia aparatów pomiarowych, [20]. Przytoczone wyżej przykłady badań naprężeń dowodzą, iż w przypadku materiałów konstrukcyjnych ze stali ferrytycznych można i należy stosować metody oparte o pomiary własności magnetosprężystych a w szczególności o efekt Barkhausena.

Podany przykład użycia mechanicznego efektu Barkhausena (MBN) dla oceny rozkładu naprężeń wewnętrznych w świadczy o tym, że jest to metoda bardzo skuteczna. Można tego typu pomiary wykonywać w trakcie np. rutynowej kampanii remontowej równolegle z pomiarami wytrzymałościowymi wycinków konstrukcji. Badania wytrzymałościowe są aktualnie prowadzone w celu ustalenia stopnia degradacji stali. Pomiar efektu mechanicznego Barkhausena jest łatwy do wdrożenia, gdyż sprowadza się do zamontowania dodatkowego czujnika na powierzchni naprężanej próbki. Otrzymane wykresy zmian natężenia MBN podczas próby rozciągania stanowią dodatkowe czytelne źródło informacji o zmianie mikrostruktury badanej stali.

Dla uzyskania tej informacji należy wykonywać pomiary natężenia MBN w zakresie stosunkowo niewielkich naprężeń. Istota wykorzystania efektu MBN dla oceny stopnia degradacji wynika wprost z faktu, iż zmiany w mikrostrukturze powstałe podczas eksploatacji danej konstrukcji, które powodują degradację własności mechanicznych - powodują również charakterystyczne zmiany własności magnetosprężystych. Zmiana mikrostruktury wpływa na rozkład naprężeń wewnętrznych wewnątrz ziarna a takie zmiany są, jak wykazano, łatwo wykrywalne i to z dużą dokładnością za pomocą efektu MBN.

Pomiar naprężeń długozasięgowych w oparciu o klasyczny efekt Barkhausena za pomocą opracowanej metody dostarcza, ze względu na swą dużą rozdzielczość, nowych możliwości w dziedzinie badań nieniszczących. Uzyskano bowiem rozdzielczość w ocenie naprężeń na poziomie kilku MPa. Podany przykład dotyczył naprężeń pozostających w złączach spawanych. Opracowana metoda daje możliwość szybkiej oceny skutków spawania a także prognozowania stanu spoiny. Podkreślić tu należy stosunkowo krótki czas pomiaru, który dla jednego punktu pomiarowego wynosi kilka sekund. Jest to czas znacznie krótszy od czasów naświetleń stosowanych w przypadku metody rentgenowskiej. Dzięki temu, można wykonywać pomiary w węzłach siatki a następnie tworzyć mapy rozkładu naprężeń, analogiczne do pokazanych na rys. 15. Podkreślić także należy istotną w wielu wypadkach dużą rozdzielczość przestrzenną metody opartej o pomiar HBN, gdyż sonda detekcyjna rejestruje sygnał z powierzchni rzędu 1 mm². Takich możliwości nie zapewnia ani metoda rentgenowska (gdzie jest stosowana wiązka o średnicy kilku mm) ani też metoda ultradźwięków ( z wiązką o średnicy około 5 mm) .

Opracowaną metodę można wykorzystać także dla oceny stanu naprężeń takich konstrukcji jak mosty czy suwnice. Możliwe jest także systematyczne monitorowanie rurociągów z gorącym medium a w szczególności miejsc narażonych na niszczące działanie korozji naprężeniowej.

5. PODSUMOWANIE

Przedstawiony we wstępie zarys klasycznej teorii własności magnetosprężystych materiałów ferromagnetycznych a w szczególności wpływu pola i naprężeń na strukturę domenową i związany z tym wpływem ruch tych granic stanowił bazę dla opisu podstawowych cech klasycznego i mechanicznego efektu Barkhausena. Te efekty są podstawą dla opracowania dwóch oryginalnych metod oceny naprężeń. Efekt mechaniczny Barkhausena (MBN) posłużył do wyznaczenia funkcji rozkładu naprężeń wewnętrznych a efekt polowy Barkhausena (HBN) wykorzystano dla oceny naprężeń długozasięgowych. Obie metody zilustrowano przykładami wyników badań przeprowadzonych dla stali niskowęglowych.

W świetle pokazanych przykładów wydaje się uzasadnione dążenie do wykorzystania obu metod w przemyśle krajowym np. dla oceny stopnia degradacji materiałów konstrukcyjnych (metoda MBN) oraz do oceny naprężeń pozostających w złączach spawanych lub naprężeń powstałych podczas eksploatacji takich konstrukcji jak np. rurociągi (metoda HBN).

Autor pragnie podziękować za owocną współpracę dr. J. CHICOIS z INSA de Lyon a także inż. M. CHMIELEWSKIEMU z Wydziału Fizyki Technicznej i dr. W. KIEŁCZYŃSKIEMU z Wydziału Mechanicznego Politechniki Gdańskiej. Część prezentowanych wyników dotyczących oceny naprężeń pozostających była uzyskana dzięki subwencji KBN (umowa nr. 9 s603 065 04).

LITERATURA

[1] R. Bozorth; "Ferromagnetism", D.Van Nostrand Company Inc., 1961.

[2] D. J. Craik, R.S. Tebble; "Ferromagnetism and Ferromagnetic Domains",

North Holland Publishing Company, 1965.

[3] A. Herpin; "Theorie du Magnetisme", Press Universitaires de France, Paris, 1968.

[4] J. Degauque; "Magnetomechanical effects and magnetomechanical damping of ferromagnetic materials", Summer School of Mechanical Spectroscopy, AGH, Kraków, 1991.

[5] J.K. Galt, C. Kittel, "Ferromagnetic domain theory. Solid State Physic", New York, Academic Press, 1956.

[6] E.W. Lee; Reports on progress in physics, 18, 184,( 1955)

[7] B.A. Liley, Phil. Mag. 41, 792 (1950)

[8] B. Augustyniak, J. Degauque; J. of Magn. .and Magn. Mater., 140-144 , 1837 (1995)

[9] D.C. Jiles; NDT International, 21, 311 (1988)

[10] J.C. McClure, Jr. K. Schr*der; CRC crit. Rev. Solid State Sci., 6, no1, 311 (1976)

[11] G. W. Smith, J.R. Birchak, J. Appl. Phys, 39, 2311 (1968)

[12] G. W. Smith, J.R. Birchak, J. Appl. Phys, 41, 3315 (1970)

[13] B. Augustyniak; J. of Alloys and Comp., 211-212, 563 (1994)

[14] B. Augustyniak; "Emisja magnetomechaniczna", w "Emisja Akustyczna", KBN, Pascal Publication, Warszawa,1994, 417-446.

[15] B. Augustyniak; Mater. Science Forum, 119-120, 559 (1993).

[16] B.Augustyniak, M. Chmielewski, D. Bednarczyk, L. Małkiński; XXII Konf. Badań Nieniszcz., Szczyrk 1993r, SIMP, 291(1993)

[17] M. Chmielewski; Wyznaczanie funkcji rozkładu naprężeń wewnętrznych ferromagnetyka za pomocą emisji magnetomechanicznej", Praca magisterska;

Politechnika Gdańska, 1992.

[18] H. Kwun ; J. of Magn. and Magn. Mater., 49, 235 (1985)

[19] A. S. Wojtas; Mat. XXII Konf. Badań Nieniszcz., Szczyrk 1993r, SIMP, 249 (1993).

[20] W. Waligóra; Seminarium "Metodyczne problemy pomiarów naprężeń własnych", Poznań, 1994, PAN, 26(1994).

I Krajowa Konferencja Podstawy Fizyczne Badań Nieniszczących, Gliwice 6-8.09.1995

17

---