Statystyka matematyczna dr Ryszard Niewczas

Zestaw pytań teoretycznych + zadanie (3,4,5,)

Plan zajęć

Powtórzyć zmienną losową i rozkład normalny

1. Elementy rachunku prawdopodobieństwa.

Zmienne losowe ciągłe i skokowe oraz ich rozkłady (normalny).

Własności parametrów rozkładów teoretycznych.

2. Wprowadzenie do statystyki matematycznej (wnioskowania statystycznego).

Estymacja punktowa.

Estymator i jego własności.

Estymacja przedziałowa.

Ogólna zasada budowy przedziałów ufności.

3. Dokładne i graniczne rozkłady statystyk z próby.

Zastosowanie w estymacji parametrów populacji generalnej.

4. Wprowadzenie do teorii weryfikacji hipotez statystycznych.

Podstawowe pojęcia i definicje.

Testy istotności dla podstawowych parametrów populacji generalnej jednowymiarowej i dwuwymiarowej.

5. Nieparametryczne testy istotności.

Test zgodności.

Test losowości.

Test niezależności.

6. Podsumowanie wykładanej treści.

Literatura podstawowa:

1. M. Sobczyk, Statystyka

2. Cz. Domańska, Metody statystyczne teoria i zadania, Uniwersytet Łódzki wyd. 6, 2001

3. K. Kukuła, Elementy statystyki w zadaniach PWN, wyd 2 , Warszawa 2003

4. S. Ostasiewicz , Z. Roszak, U. Siedlwecka, Statystyka. Elementy teorii i zadania. Akademia Ekonomiczna, Wrocław 1998

Literatura uzupełniająca:

1. J. Jóźwiak, J. Podgórski, Statystyka od podstaw. Wyd. 5, PWE, Warszawa 1997

2. M.H. Aczel , Statystyka w zarządzaniu, PWN, Warszawa 2005

3. A. Zeljaś, Metody statystyczne, PWE, Warszawa 2002

4. J. Greń, Statystyka matematyczna modele i zadania. Warszawa, 1982

5. R. Zieliński, Tablice matematyczne, Wyd. 2, PWN, Warszawa

Wnioskowanie statystyczne związane jest z próbą losową a zatem korzystamy z metod wnioskowania statystycznego.

Próbę losową pozyskujemy w wyniku zastosowania mechanizmu losowego doboru jednostek, musi być ona odpowiednio liczna, aby można było ją uznać za reprezentatywną.

n- liczebność próby

N- liczba jednostek w populacji generalnej

Sposób jednostek do próby:

-losowanie zależne (wylosowana jednostka nie wraca do puli),

-losowanie zależne (wylosowana jednostka wraca do puli),

-losowanie indywidualne (wybieramy do próby pojedyncze jednostki)

-losowanie zespołowe (wybieramy grupy jednostek)

Bazą z której dokonuje się doboru jednostek do próby jest operat losowania. Operat losowania to wykaz wszystkich jednostek wchodzących w skład populacji generalnej. Poszczególne jednostki - elementy losowania - zostają najczęściej ponumerowane. Wyboru poszczególnych elementów do próby dokonujemy najczęściej za pomocą specjalnie skonstruowanych tablic liczb losowych.

Rozkład z próby - podstawowe pojęcia.

Przestrzeń prób losowych jest to zbiór n elementowych prób utworzonych z populacji generalnej liczącej N jednostek( zazwyczaj jest to zbiór nieskończony).

Statystyka z próby jest to wielkość charakteryzująca próbę (np. średnia, mediana dominanta). Statystyka z próby jest zmienną losową. Np.

1 2 3

x₁ x₂ x₃

Zmienna losowa to zmienna, która może przybierać różne wartości z określonym prawdopodobieństwem.

Rozkład statystyki jest to teoretyczny rozkład prawdopodobieństwa zmiennej losowej będącej statystyką. Rozkład ten zależy od rozkłady zmiennej losowej w populacji, z której pochodzi próba, oraz od wielkości próby.

Klasyczny podział próby

Mała próba duża próba

n< 30 n >30

Rozkład graniczny statystyki jest to rozkład, który otrzymuje się przy założeniu nieograniczenie dużej próby n → ∞. Jest to rozkład, do którego przybliża się rozkład danej statystyki, gdy n → ∞. Rozkład graniczny nazywany jest także rozkładem asymptotycznym. ( np. rozkład normalny jest rozkładem granicznym rozkładu

t- studenta).

Rozkłady z dużych prób.

Jeżeli rozkład zmiennej losowej X jest opisany za pomocą rozkładu normalnego to najczęściej mamy doczynienia z rozkładami normalnymi z prób opisywanych statystyk lub z rozkładami asymptotycznie normalnymi

Przykład

Jeżeli interesuje nas parametr średnia arytmetyczna z populacji generalnej to rozkład średniej z prób dużych jest opisany rozkładem normalnym Θ =
. Naszą statystyką jest
.

Rozkład średniej z próby
_11
21
31

Rozkład normalny N[ E(
), D (
)]

E(
)- wartość oczekiwana

D(
) odchylenie standardowe zmiennej losowej

Gdzie

E(
) = E(X)

n - wielkość próby

Rozkład normalny przyjmuje postać N[E(X), D(
)]

Rozkład z małych prób.

W zależności od parametru Θ rozkład z próby danej statystyki może być opisany za pomocą różnych rozkładów teoretycznych.

Przykład

Jeżeli zmienna losowa x jest opisana z pomocą rozkładu normalnego o znanej wartości oczekiwanej E(X) ale o nie znanych odchyleniach standardowych δ(X) to średnia arytmetyczna z prób losowych ma rozkład :

1. Normalny w przypadku dużej próby o parametrach

N[E(X),
)]

S - odchylenie standardowe dla próby losowej

Gdzie

E(
) = E(X)

2. rozkład t- studenta w przypadku małej próby o parametrach

N[E(X),
)]

S - odchylenie standardowe dla próby losowej

Gdzie

E(
) = E(X)

Inne rozkłady statystyk z próby:

1. Rozkład wariancji z próby opisywany jest rozkładem chi² (Χ²).

2. Rozkład ilorazu wariancji opisywany był by rozkładem F-Snedecora

Wnioskowanie statystyczne

Teoria estymacji(szacowania) Teoria weryfikacji hipotez statystycznych

Założenia

Próba powinna być reprezentatywna tzn uzyskana zgodnie z wymogami metody reprezentatywnej.

Próbę uznajemy za reprezentatywną, gdy jest:

1. Losowa.

2. Dostatecznie liczna.

Wymogi:

1. Rozkład badanej próby jest normalny N[E(X),δ(X)].

2. Próba jest prosta tzn. uzyskana w wyniku korzystania z mechanizmu losowania zwanego losowaniem prostym.

Losowaniem prostym nazywamy losowanie indywidualne nieograniczone i niezależne( ze zwracaniem)

Losowaniem systemtycznym

Podstawy teorii estymacji.

Estymacja jest to podstawowy rodzaj wnioskowania statystycznego polegający na szacowaniu parametrów populacji generalnej bądź postaci funkcyjnej rozkładu populacji na podstawie wyników próby losowej.

Rodzaje estymacji:

1. parametryczna

2. nieparametryczna

Techniki estymacji:

a) estymacja punktowa polega na podaniu wielkości szacowanego parametru, która jest równa wartości estymatora Θ = T. Ponieważ z reguły wielkość estymatora różni się od wartości parametru populacji generalnej , podaje się jednocześnie średni błąd szacunku, czyli odchylenie standardowe estymatora T_n

Θ = T + D(Tn)

gdzie:

T- ocena parametru( wartość estymatora dla danej próby)

Tn - estymator

D(Tn) - błąd szacunku estymatora (odchylenie standardowe estymatora)

Dzięki temu uzyskujemy konkretna wartość.

b) estymacja przedziałowa polega na skonstruowaniu pewnego przedziału liczbowego, zwanego przedziałem ufności, który z określonym prawdopodobieństwem pokryje estymowany parametr. Jeśli granice tego przedziału oznaczymy przez kd i kg wówczas możemy zapisać go następująco:

P{kd < Θ <kg} = 1-α

kd - dolna granica przedziału ( kres dolny)

kg - górna granica przedziału ( kres górny)

1-α -współczynnik ufności ( to prawdopodobieństwo z jakim parametr Θ pokryty jest tym przedziałem) może on przybrać wartości 0,90 0,95 0,99

Jeżeli rozkład estymatora opisywany jest za pomocą rozkładu normalnego to przedział ufności zapisujemy następująco:

P{T - u_αD(Tn) < Θ < T + u_αD(Tn)}= 1 - α

u_α - wartość zmiennej standaryzowanej rozkładu normalnego dla danego α (α ≤ 0,10)

Estymator jest to funkcja wyników z próby lub inaczej statystyka służąca do oszacowania nieznanej wartości parametru Θ. Wartość estymatora dla próby losowej jest zmienną losową.

Rozkład estymatora zależy od:

1. Rozkładu badanej zmiennej losowej.

2. Schematu losowania.

3. Wielkości próby.

Własności estymatora:

1. Nieobciążoność - estymator jest nieobciążony jeżeli wartość oczekiwana jego rozkładu jest równa nieznanemu parametrowi populacji generalnej E (Tn) = Θ

Wyrażenie B(Tn) = E(Tn) - Θ nazywamy obciążeniem estymatora.

Estymator jest asymptotycznie nieobciążony gdy
jeżeli jego obciążenie maleje wraz ze wzrostem próby.

2. Zgodność estymatora oznacza że wraz ze wzrostem liczebności próby ,z której go wyznaczamy, jego wartość będzie zbliżała się do wartość będzie zbliżała się do wartości nieznanego parametru zbiorowości całkowitej.

ε- dowolnie mała stała

3. Efektywność - estymator jest tym efektywniejszy, im jego zróżnicowanie , które możemy mierzyć wariancją , jest mniejsze. Im mniejsze będzie zróżnicowanie estymatora tym nasze sądy o populacji generalnej na jego podstawie będą bardziej trafne.

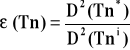
D² (Tn^*) - wariancja najefektywniejszego estymatora ( wtedy gdy dany jest zamknięty zbiór estymatorów)

D² (Tnⁱ) - wariancja i - tego estymatora

0< ε(Tn)

Jeżeli efektywność naszego estymatora zmierza do jedności to możemy powiedzieć że estymator jest najefektywniejszy asymptotyczne

4. Dostateczna wystarczalność - estymator parametru Θ jest dostatecznie wystarczalny jeżeli zawiera wszystkie informacje jakie na temat parametru Θ występują w próbie.

(najlepszym estymatorem jest średnia )

Estymacja wybranych parametrów

1. Przedział ufności dla średniej.

Założenia - rozkład zmiennej losowej jest rozkładem normalnym, próba jest prosta.

Rozkład estymatora

. δ(X)- znane δ(X)- nieznane

próba dowolna, rozkład normalny trzeba skorzystać z odchylenia

standardowego estymatora

dla dużej próby (n>30) dla małej próby (n ≤ 30)

Rozkład normalny (S) Rozkład t- studenta (S Ŝ)

Parametr: Θ =
= E(X) = m

Estymator Tn =
=

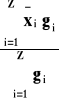
Ocena parametru Tn =
= a - policzalna wartość średniej

Konstrukcja przedziału ufności przy znanym odchyleniu standardowym dla zmiennej losowej.

Wartość funkcji gęstości dla u

P { - u _α < u < u _α } 1- α

Definicja

dla zmiennej losowej

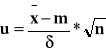
dla rozkładu struktury

Przedział

Po uwzględnieniu znaku stojącego przy u_α otrzymujemy ostatecznie

Metody znajdowania estymatorów:

1. metoda momentów,

2. metoda największej wiarygodności,

3. metoda najmniejszych kwadratów,

4. metoda Bayesa

Rodzaje estymatorów:

1. liniowy

2. ilorazowy

3. regresyjny

4. bayesowski

Wykład 2

(estymacja średniej, wsk struktury, testy istotności)

Test dla dwóch wskaźników struktury.

Przykład

W pewnym roku na egzaminie wstępnym z matematyki na wyższą uczelnię spośród 560 absolwentów techników 240 nie rozwiązało pewnego zadania, natomiast na 1040 zdających absolwentów liceów ogólnokształcących nie rozwiązało tego zadania 380 kandydatów. Na poziomie istotności α = 0,05 zweryfikować hipotezę o jednakowym stopniu opanowania tej partii matematyki której dotyczyło to zadanie przez absolwentów obu typów szkół.

Dane:

Technikum Liceum

n₁ = 560 n₂ = 1040

m₁ = 240 m₂ = 380

α = 0,05

1.Układ hipotez

H₀ : p₁ ≠ p₂

H₁ : p₁ = p₂

2. Duża próba n > 30

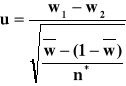
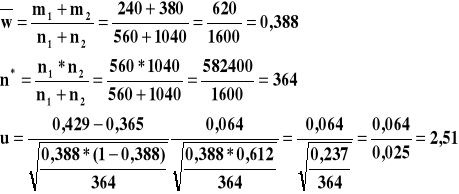
3. Określenie poziomu istotności

Dla pewnego α = 0,05 szukamy wartości krytycznych dla u_α w taki sposób by prawdopodobieństwo P {׀u׀ ≥ u_α } = α.

Obszar krytyczny jest dwustronny, rozkład statystyki musi być symetryczny

F- dystrybuanta

u_{α = 0,05}=1,96

Obszar krytyczny (

Jeżeli wystąpi ׀u׀ ≥ u_α to H₀ odrzucamy na korzyść H₁

Jeżeli ׀u׀< u_α to brak podstaw do odrzucenia hipotezy H₀

׀u׀ = 2,51 u_α =1,96 ׀u׀ ≥ u_α H₀ odrzucamy na korzyść H₁

Przy poziomie istotności α = 0,05 możemy twierdzić że stopień opanowania pewnej partii matematyki jest różny. Absolwenci liceów opanowali tę partię materiału lepiej bo dla nich wskaźnik struktury jest niższy.

A) Zweryfikować hipotezę że absolwenci liceów lepiej opanowali pewną matematyki niż absolwenci techników

H₀ = p₁ =P₂

H₁ = p₁ =P₂

Nieparametryczne testy istotności

Test losowości służy do badania losowego charakteru próby tzn czy można uznać daną próbę za losową czy nie.

Przykład

Zbadano grupę 15 studentów pod względem wzrostu:

165,180,180,175,177,195,170,182,187,173,178,190,188,175,182

czy jest to próba losowa ? Przyjąć poziom istotności 0,05

Rozwiązanie:

a) układ hipotez

H₀ próba losowa

H₁ próba nielosowa

b) statystyką sprawdzającą jest liczba serii:

• wyznaczam pozycję mediany

• wyznaczamy medianę

Porządkuję szereg rosnąco

165	180	180	175	177	195	170	182	187	173	178	190	188	175	182
165	170	173	175	175	177	178	180	180	182	182	187	188	190	195
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
A			A	A	B	A	B	B	A	A	B	B	A	B
1					2	3	4		5		6		7	8

A gdy x_i < Me

B gdy x_i > Me

Uwaga: x_i = Me pomijamy

Seria jest to ciąg jednakowych liter ( sytuacji). Seria może być jednoelementowa

Me = X₈ = 180

n = 13 bo 15-2 = gdyż pomijamy wartości równe medianie

k = 8

c) α, k_α, P{k ≤ k_α }= α odczytujemy z tablic rozkładu serii dla α, oraz n₁ i n₂

n₁ liczba sytuacji oznaczonych literą A

n₂ liczba sytuacji oznaczonych literą B

Ostatecznie mamy

n₁ = 7 n₂ = 6 k_0,05 = 3

d) k ≤ k_α k=8 > k_0,05 =3

Decyzja nie ma podstaw do odrzucenia hipotezy H₀

ODP Przy poziomie istotności α = 0,05 nie mamy podstaw do odrzucenia hipotezy głoszącej że próba jest losowa.

Test medianowy z dwustronnym obszarem krytycznym jest lepszy od poprzedniej wersji bowiem reaguje na obserwowalną powtarzalność czyli tendencję

Przykład treść jw

a) układ hipotez

H₀ próba losowa

H₁ próba nielosowa

b) statystyką sprawdzającą jest liczba serii:

• wyznaczamy medianę

• tworzymy ciąg złożony z liter A i B gdzie

A gdy x_i < Me

B gdy x_i > Me

Uwaga: x_i = Me pomijamy

Me = X₈ = 180

n = 13 bo 15-2 = gdyż pomijamy wartości równe medianie

k = 8

Uwaga: x_i = Me pomijamy

Seria jest to ciąg jednakowych liter ( sytuacji). Seria może być jednoelementowa

c) α ,K₁ P{K ≤ K₁ } = α/2

K₂ P{K ≤ K₂ } = 1- α/2

Rozkład serii nie jest rozkładem symetrycznym, dlatego należy odczytać dwie wartości krytyczne dla lewostronnego obszaru krytycznego przy n₁ i n₂

d) jeżeli K ≤ K₁ lub K > K₂ to odrzucamy hipotezę H₀

K₁ < K ≤ K₂ to nie mamy podstaw do odrzucenia

-α/2 α/2

K₁ K₂

α/2 = 0,05/2 = 0,025

K₁ = K _{α/2 = 0,025} =3 n₁ = 7

K₂ =K_{1 - α/2 = 0,975} =10 n₂ = 6

d) K₁ = 3 < K =8 < K₂ = 10 nie mamy podstaw do odrzucenia hipotezy

Przykład 2 (test z serii z dwustronnym obszarem krytycznym)

W kolejce po świadectwa udziałowe zaobserwowano mężczyzn i kobiety według następującego porządku

M K M K M M M K K M K M K M K M M M M K M K M K M M K K K M

Na poziomie istotności 0,05 sprawdzić hipotezę głoszącą że ciąg ten jest losowy.

Rozwiązanie

a) układ hipotez

H₀ ciąg losowy

H₁ ciąg nielosowy

b) statystyką sprawdzającą jest liczba serii:

M	K	M	K	M	M	M	K	K	M	K	M	K	M	K	M	M	M	M	K		M		K		M		K		M		M
1	2	3	4	5			6		7	8	9	10	11	12	13					14		15		16		17		18		19
K	K	K	M
20			21

Ustalamy liczbę serii K = 21

c) α ,K₁ P{K ≤ K₁ } = α/2

K₂ P{K ≤ K₂ } = 1- α/2

K₁ = K _{α/2 = 0,025} = 8 n₁ = 17

K₂ = K_{1- α/2 = 0,975} = 19 n₂ = 13

d) K=21 > K₂ = 19

Decyzja odrzucamy hipotezę H₀

ODP Na poziomie istotności 0,05 możemy twierdzić że ciąg ten jest nie losowy, układ kolejnych kolejkowiczów był tendencyjny.

Rozkład normalny zmiennej standaryzowanej

N(0,1)

H₁ : A ≠ B P { |u| ≥ u_α } α obszar dwustronny

F{ (u_α) = 1 - α/2 u_α dystrybuanta obszar krytyczny

H₁ : A > B P { u ≥ u_α } α obszar prawostronny

F{ (u_α) = 1 - α u_α

H₁ : A < B P { u ≤ u_α } α obszar prawostronny

F{ (-u_α) = α u_α

Testy zgodności

Jest to obszerna grupa testów do badania rozkładów.

Badanie zgodności dowolnego rozkładu :

1. empirycznego z zakładanym rozkładem teoretycznym (trzeba patrzeć jakiej zmiennej on dotyczy , zmienna losowa może być dowolna lub tylko ciągła)

2. Testy służące do badania zgodności dwóch lub więcej rozkładów empirycznych ( czy nasze próby pochodzą z populacji o tym samym rozkładzie, jeśli tak to próby możemy łączyć w większe)

Testy możemy podzielić na klasyczne, podstawowe, i nowoczesne.

Testy możemy także ze względu na wielkość próby czyli związane z małą lub z dużą próbą.

Klasyczne testy zgodności rozkładu empirycznego z rozkładem teoretycznym:

1. test zgodności χ² do badania normalności rozkładu ( uniwersalny test dla dowolnej zmiennej losowej

2. test zgodności λ Kołmogorowa ( służy do badania zgodności dwóch rozkładów empirycznych dla zmiennej losowej ciągłej)

3. test zgodności Kołmogorowa - Smiernowa

Nieparametryczne testy zgodności

Test klasyczny - test zgodności χ²

Założenia:

1. Dowolna zmienna losowa

2. Duża próba n>30 ( grubo powyżej)

3. Każdej klasie ( wariantowi ) musi być przyporządkowane n_i ≥ 8, jeśli tak nie jest to należy łączyć liczebności z sąsiednich klas

1. układ hipotez

H₀ : F(x) = F₀ (x)

H₁ : F(x) ≠ F₀ (x)

Gdzie: F₀ (x) dystrybuanta rozkładu teoretycznego w punkcie x

2. Statystyka sprawdzająca test zgodności χ²

Postać testu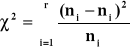

Gdzie
liczebność teoretyczna

n_i ≥ 8

3. α,χ² P{ χ² > χ² ≥
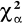
   }=α

u = r - l -1

gdzie l- liczba szacowanych parametrów rozkładu teoretycznego

4. Obszar krytyczny określa nierówność χ² ≥
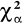
   gdzie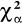
   jest wartością krytyczną odczytana z tablic rozkładu χ² dla z góry ustalonego poziomu istotności. Gdy χ² ≥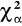
   odrzucamy hipotezę H₀ gdy χ² <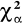
   przyjmujemy hipotezę zerową

Przykład

Koszty materiałowe w pewnej gałęzi gospodarki narodowej przy produkcji pewnego wyrobu były w wylosowanych 120 zakładach następujące ( w zł)

Koszt materiałowy	Liczba zakładów
150 - 250	7
250 - 350	10
350 - 450	21
450 - 550	30
550 - 650	19
650 - 750	15
750 - 850	10
850 - 950	6
950 - 1050	2
	Σ 120

Na poziomie istotności 0,10 zweryfikować hipotezę głoszącą że rozkład kosztów materiałowych przy produkcji tego wyrobu jest normalny N(540, 200)

Rozwiązanie:

Dane: n = 120 α = 0,10 N(540,120) E(x) = 540 (wartość oczekiwana) δ (x) = 120 ( odchylenie standardowe

1. układ hipotez

H₀ : F(x) = F_N (x)

H₁ : F(x) ≠ F_N (x)

Gdzie: F₀ (x) dystrybuanta rozkładu normalnego w punkcie x

2. Statystyka sprawdzająca test zgodności χ²

Postać testu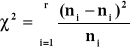

p_i = F(u_i) - F(u_i-1)

Wyjątek

p₁ = F( u₁)

Uwaga przy znanych parametrach rozkładu normalnego możemy łączyć klasy już od początku by n_i ≥ 8

Klasy które zostały połączone

1. 2. 3.. p2 = (F(u3) - F(u2) = 0,326 - 0,171 = 0,155 4. Liczymy liczebności teoretyczne 5. Liczymy cząstkowe wartości statystyki

3. α,χ² P{ χ² ≥
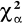
   }=α

u = r-l - 1 = 7 - 0 - 1 = 6

7- bo siedem pozycji, l nie występuje gdyż ten typ statystyki ma jeden stopień swobody

4. Otrzymyjemy:

χ² = 3,82 α = 0,10
= 10,645

5. χ² = 3,82 ≥
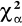
   = 10,645

Decyzja niema podstaw do odrzucenia hipotezy H₀

ODP Na poziomie istotności 0,10 nie mamy podstaw do odrzucenia hipotezy głoszącej że rozkład kosztów materiałowych przy produkcji tego wyrobu jest normalny.

Przykład

Treść jak wyżej ale nie znamy parametrów rozkładu normalnego

1. układ hipotez

H₀ : F(x) = F_N (x)

H₁ : F(x) ≠ F_N (x)

Gdzie: F₀ (x) dystrybuanta rozkładu normalnego w punkcie x

2. Statystyka sprawdzająca test zgodności χ²

Postać testu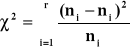

p_i = F(u_i) - F(u_i-1)

p₁ = F(u₁)

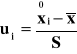
Obliczam wartość średniej

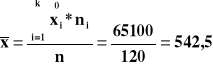
Obliczam odchylenie standardowe

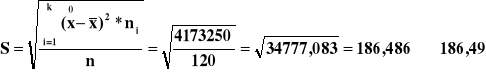
Statystyka χ² =3,783

3. α,χ² P{ χ² ≥
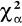
   }=α

Obliczam liczbę stopni swobody

u = r - l - 1 = 7 - 2 - 1 = 4

7 bo złączyłem dwie klasy , 2 bo szukam dwóch parametrów

χ² = 7,779

5. Otrzymujemy

χ² = 7,779 α = 0,10
= 7,779

Decyzja nie ma podstaw do odrzucenia hipotezy H₀

6. Odp Przy poziomie istotności 0,10 nie mamy podstaw do odrzucenia hipotezy głoszącej, że rozkład kosztów materiałowych przy produkcji tego wyrobu jest rozkładem normalny.

Można przeliczyć to samo zadanie dla N( E(x),200) lub N(540,δ(x))

Wykład dodatkowy zadania

Zad 1

Estymacja wskaźnika struktury

W pewnym mieście wylosowano 500 mieszkań. Stwierdzono że 200 spośród nich było wyposażonych w telefon . Czy na tej podstawie można coś powiedzieć o odsetku mieszkań wyposażonych w telefon w tym mieście? Przyjmij współczynnik ufności na poziomie 0,99.

Rozwiązanie:

n = 500 m = 200 1-α = 0,99

Wersje rozwiązań

1. bezkrytyczna

- sprawdzamy czy n > 100

2. krytyczna

• sprawdzamy czy n > 100

• sprawdzamy czy m jest wystarczające

• sprawdzamy czy próba jest losowa

• o jaki telefon chodzi

Wniosek : Wobec braku możliwości rozstrzygnięć wątpliwości poza formalnie wymaganą wielkością próby zadanie rozwiązujemy tak jak w wersji bezkrytycznej.

Obliczam wartość wskaźnika struktury:

0,05 < w_i < 0,95

Obliczam wartość u

w_i -Δ = 0,4 - 0,057 = 0,343

w_i -Δ = 0,4 + 0,057 = 0,457

0,343 < p < 0,457

34,3 % < p % < 45,7 %

Odp Z ufnością 0,99 przedział o końcach 34,3 % oraz 45,7% pokryje odsetek mieszkań wyposażonych w telefony w tym mieście.

Zad 2

Test dla wskaźnika struktury w populacji

W jednej z politechnik wylosowano niezależnie próbę 150 studentów, z których jedynie 45 zdało wszystkie egzaminy w pierwszym terminie. Na poziomie istotności 0,05 zweryfikuj hipotezę głoszącą że mniej niż jedna trzecia część studentów zdaje egzaminy za pierwszym podejściem.

Rozwiązanie:

n = 150 m = 45 α = 0,05 p₀ = 1/3 = 0,333

Uwaga sprawdzam czy n > 100

Obliczam wartość wskaźnika struktury

Sprawdzam czy w_i < p₀ 0,300 < 0,333

1. układ hipotez

H₀ : p = p₀

H₁ : p ≠ p

2. Statystyka sprawdzająca

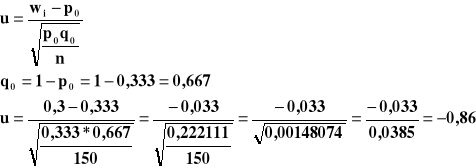
3. α, u_α , p{u ≤ u_α}= α

F(-u_α) = α = 0,05

u_{α = 0,05} = -1,64

4. u > u_α u = - 0,86 > u_{α = 0,05} = -1,64

Decyzja nie ma podstaw do odrzucenia hipotezy H₀

5. Odp Przy poziomie istotności 0,05 nie mamy podstaw do odrzucenia hipotezy głoszącej że jedna trzecia studentów zdaje egzaminy za pierwszym razem

Zad 3

Test dla dwóch wskaźników struktury

Na 150 wypadków samochodowych w jednym województwie 118 spowodowanych było nadużyciem przez kierowców alkoholu. W drugim województwie liczba wypadków spowodowanych przez tę samą przyczynę wyniosła 130 na 185 zgłoszonych. Na poziomie istotności 0,05 zweryfikuj hipotezę, że odsetek wypadków drogowych spowodowanych nadużyciem alkoholu w obydwu województwach jest identyczny.

Dane

n₁ = 150 m₁ = 118

n₂ = 185 m₂ = 130 α = 0,05

Uwaga sprawdzamy czy

n₁ >100

n₂ > 100

1. układ hipotez

H₀ : p₁ = p₂

H₁ : p₁ ≠ p₂

2. Statystyka sprawdzająca

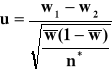
1. 3. α, u_α , p{|u | ≥ u_α}= α

F(u_α) = 1 - α/2 = 1- 0,05/2 = 0,975

u_{α = 0,05} = 1,96

2. |u | = 1,74 < u_α= 1,96

Decyzja: nie ma podstaw do odrzucenia H₀

Odp Przy poziomie istotności 0,05 brak podstaw do odrzucenia hipotezy głoszącej że odsetek wypadków spowodowanych nadużyciem alkoholu jest w obydwu województwach jednakowy

1

---