Tomasz Pajączkowski

15.05.2001

Ćwiczenie nr 2b.

Temat: Pomiar przyspieszenia ziemskiego za pomocą wahadła rewersyjnego.

Tabela wartości:

	czas t [s]			czas t' [s]
d [cm]	47	46	45	47	45	46
	14,015	13,91	13,787	14,02	13,921	13,776
	14,022	13,911	13,785	14,023	13,921	13,777
	14,023	13,909	13,784	14,023	13,92	13,775
	14,022	13,91	13,784	14,024	13,91	13,774
	14,022	13,909	13,784	14,022	13,919	13,774
	14,023	13,911	13,783	14,023	13,918	13,775
	14,023	13,909	13,781	14,023	13,918	13,774
	14,019	13,909	13,781	14,023	13,918	13,775
	14,019	13,908	13,782	14,023	13,92	13,773
	14,02	13,908	13,781	14,024	13,92	13,773
Σ	140,208	139,094	137,832	140,228	139,185	137,746

Teoria zjawiska:

Przez ciężar ciała rozumiemy siłę z jaką Ziemia przyciąga dane ciało. Siła ta nadaje swobodnie spadającemu ciału przyspieszenie g zwane przyspieszeniem ziemskim. Wartość tej siły można przedstawić wzorem: F = mg.

Wartość przyspieszenia ziemskiego nie jest stała, ale zależy od położenia punktu na powierzchni Ziemi. Przyczynami tego zjawiska są: a) spłaszczenie kuli ziemskiej, b) ruch obrotowy Ziemi, c) niejednorodność budowy Ziemi.

Jak wiadomo Ziemia ma kształt zbliżony do elipsoidy obrotowej, spłaszczonej od strony biegunów geograficznych, w skutek tego wartość g zależy od szerokości geograficznej i jest największa na biegunie, a najmniejsza na równiku.

Ruch obrotowy Ziemi powoduje powstanie siły odśrodkowej, która zmniejsza ciężar każdego ciała znajdującego się na Ziemi. Siła odśrodkowa jest prostopadła do osi ziemskiej, a więc jej kierunek względem poziomu zależy od szerokości geograficznej. Zmniejszenie ciężaru ciała jest największe na równiku i w miarę zbliżania się do bieguna maleje do zera.

Wartość g zmienia się w skutek działania tych dwóch czynników od wartości ok. 9,78m/s² na równiku do ok. 9,83m/s² na biegunie.

Niejednorodność budowy Ziemi, jak i również ukształtowanie powierzchni Ziemi powodują niewielkie lokalne wahania wartości g.

Wahadłem fizycznym ( jest nim wahadło rewersyjne ) nazywamy bryłę sztywną wahającą się wokół osi obrotu nie przechodzącej przez jej środek masy. Ruch tego wahadła będzie ruchem obrotowym, toteż dynamiczne równanie ruchu będzie miało postać wzoru: M = I ε.

Rozważmy siły działające na wahadło fizyczne ( jak przedstawione to zostało na poniższym rysunku ). W środku masy C jest przyłożona siła ciężkości, której składowa F₁ jest równoważona siła przyłożoną w punkcie zawieszenia wahadła. Składowa F₂ siły ciężkości, prostopadła do prostej będącej promieniem wodzącym środka masy bryły względem osi obrotu, prostopadłej do płaszczyzny rysunku i przechodzącej przez punkt zawieszenia wahadła, powoduje ruch drgający tego wahadła. Jej moment względem punktu O będzie więc figurował w dynamicznym równaniu ruchu wahadła. Ponieważ sinα jest dla małych kątów równy kątowi α wyrażonemu w mierze łukowej, a w ruchu obrotowym wahadła wychylenie jest określone właśnie przez kąt α, więc siła F₂ będzie dla małych kątów siłą quasi-sprężystą, a drgania wahadła będą drganiami harmonicznymi.

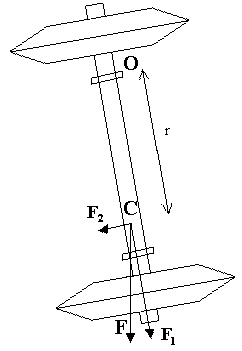
Wyprowadzenie wzoru roboczego:

Z powyższego moment siły F₂ względem osi przechodzącej przez O jest

M = F₂r = Fr sinα = mgr sinα ,

gdzie m oznacza masę wahadła. Oznaczając przez x długość łuku, o jaki odchyli się masa od położenia równowagi, przy małych kątach α możemy przyjąć, że sinα = x/r, stąd moment siły będzie równy: M = mgx.

Przyspieszenie liniowe a punktu odległego o r od osi obrotu wynosi a = εr, stąd ε = a/r. Podstawiając powyższe wartości do dynamiczne równanie ruchu otrzymamy:

mgx = Ia/r

a = mgrx/I

Z takim przyspieszeniem porusza się więc środek masy wahadła fizycznego. Na podstawie rozważań dotyczących wahadła matematycznego ( opracowanie ćwiczenia 2a i 2b ) można wykazać, że przyspieszenie kulki wahadła matematycznego o długości l wynosi: a = gx/l.

Wahadło matematyczne o takiej długości ma się w każdej chwili poruszać z takim przyspieszeniem i fazą, jak rozważane obecnie wahadło fizyczne. Jeżeli w każdej chwili oba wahadła mają to samo przyspieszenie i tę samą fazę, to poruszają się zupełnie jednakowo, w szczególności mają taki sam okres wahań.

Z porównania wartości przyspieszenia mamy:

mgrx/I = gx/l

l = I/mr

Wahadło matematyczne o takiej długości będzie więc wahać z takim samym okresem, jak wahadło fizyczne. Wielkość l określoną powyższym wzorem nazywamy długością zredukowaną wahadła fizycznego i oznaczamy d. W związku z powyższym:

T = 2π(I/mrg)^1/2 = 2π(d/g)^1/2

stąd: g = 4π²d/T²

Okres wahadła obliczamy ze wzoru: T = (T₁ + T₂)/2

Opis ćwiczenia z opisem wykonanego eksperymentu:

Celem ćwiczenia było wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego. Cały pomiar przy wykorzystaniu tej metody sprowadza się do wyznaczenia okresu wahadła T.

Przed przystąpieniem do wykonywania ćwiczenia należy odchylić wahadło o 4-5° i zmierzyć jego okres, poczym obrócić je o 180°, ustawić na drugim ostrzu i zmierzyć jego okres T₂, celem ich porównania. Różnica ich nie powinna przekraczać 0,5%, w przeciwnym razie należy skorygować położenie ostrzy.

W przypadku zgodności okresów można przystąpić do wykonywania zasadniczych pomiarów, powtarzając je dla obu położeń wahadła przynajmniej 10 razy. W tym celu należy przesunąć ostrze o 1, 2, 3 cm i dla każdego z tych położeń ostrza wyznaczyć wartość czasu t dla tej samej liczby okresów.

Przy dużym zautomatyzowaniu aparatury jaką dysponowaliśmy możliwe było uzyskanie bardzo dokładnych, powtarzalnych wartości eksperymentalnych. Co niewątpliwie winno mieć swoje odzwierciedlenie w końcowej wartości g.

Uzyskane wyniki zebrałem w powyższej tabeli a następnie na ich podstawie dokonałem końcowych obliczeń i wyciągnąłem ostateczne wnioski.

Obliczenia do wykonanego ćwiczenia:

T = 1,402s dla d = 0,47m

T = 1,392s dla d = 0,46m

T = 1,378s dla d = 0,45m

w powyższym można przyjąć, T = 1,40s

Podstawiając tę wartość do powyższego wzoru otrzymujemy: g = 9,44m/s²

g = 9,37m/s²

g = 9,36m/s²

średnia wartość g = 9,39m/s²

Szacowanie niepewności pomiaru:

Δx(t) = 0,001s

U_B(t) = Δx(t)/3^1/2 = 0,0058s

U_A(t) = U_A(t) = [ Σε²/n(n-1) ]^1/2 = 0,00002 s

U_C(T) = 0,00058s

Δx(d) = 0,1·10^-2m

U_C(d) = Δx(d)/3^1/2 = 0,1·10^-2/3^1/2 = 0,00058m

Wyznaczanie pochodnych cząstkowych:

ðg/ðT = 8π²d/T³ = 13,52m/s³

= 13,23m/s³

= 12,95m/s³

ðg/ðd = 4π²/T² = 20,14 1/s²

U_C(g) = [ (ðg/ðT)² U_C²(T) + (ðg/ðd)² U_C²(d) ]^1/2 = 0,014m/s²

= 0,014m/s²

= 0,014m/s²

dla α = 0,95

U = 2· 0,014m/s² = 0,028m/s²

Ostatecznie g = ( 9,390 ± 0,028 ) m/s²

Wnioski:

Wyznaczona wartość przyspieszenia ziemskiego wynosi g = ( 9,390 ± 0,028 ) m/s². Wartość ta, choć zbliżona do wartości rzeczywistej nieznacznie różni się od niej. Spowodowane to może być małą dokładnością przyrządu jak również przybliżeniami wartości pośrednich.

F₁ = mg cosα

F₂ = mg sinα

---