032 033

O32    ........._f _    ,

angielskie, szczególnie rozpowszechnione w literaturze technicznej, oparte na spójnikach zdaniowych (patrz p. 1.3.4.1).

Dla liczby argumentów większej nil 2 istnieją też inne funkcje o dużym znaczeniu praktycznym, np. większościowa (Uajority), przyjmująca wartość 1, g'dy większość argumentów równa jest 1, mniejszościowa (Mlnority), parzystości (Even Parity), równa 1, gdy parzysta liczba argumentów równa jest 1, czy nleparzystości (Odd Parity),

1.3.3, Postacie kanoniczne funkcji logicznej

Każdą funkcję logiczną można zawsze rozłożyć ną składniki, według. zasady¹^ ,    ...

f(x₁,x₂,...,x_a) m X₁'f(1,X₂,...,X_a) ♦ X₁¹f(0,X₂,...,X_n)    .(1.8)

Kontynuując ten rozkład aż do wyczerpania listy zmiennych uzyskujemy ostatecznie

f(x₁,¹₂,...,x_a) =x₁x₂'...x_n«f(1,1,...,1) +

+ x^x₂ ... x_n‘ f(0,1,...,1) ♦ ... +    f(0,0, ...,0)    (1.9)

Przyporządkowując każdemu pełnemu iloczynowi (zawierającemu wszystkie zmienne'z negacją.lub bez) liczbę binarną wg zasady

x_fc-1,    x_k—~ 0    (1.10)

mażemy, go oznaczyć symbolem 1^, gdzie indeks i reprezentuje wartość dziesiętną uzyskanej liczby binarnej (numer iloczynu). Np. pełnemu iloczynowi Łjżycj odpowiada liczba (101 )₂ = (5)^o^{1 a}    ^leśy 6° oznaczyć symbo

lem I^.

Oznaczając również

f (próbka wartości zmiennych) =    _prółJkl

(np. f(0TT)/= aj); wzór (1.9) można zapisać w postaci

2ⁿ-f

f(¹-|iX2^,1v^,1n) ⁼ J] ^at^{1 1}i i<o ..

Ponieważ e {0,T| , więc sumowanie można przeprowadzać tylko po tych indeksach 1, dla których o_Ł = 1, co symbolicznie zapisujemy w postaci

f(x₁,x₂,..._tz_Q) = y    (1.11)

V: ■

Każdą funkcję .logiczną można więc przedstawić w postaci sumy pełnych iloczynów, odpowiadających — zgodnie z przyporządkowaniem. (1.10)    - tym

próbkom wartości zmiennych, przy których-funkcja ta przyjmuje wartość 1. Takie przedstawienie jest Jedną z postaci kanonicznych funkcji logicznej 1 nazywa się zupełna normalna postacią sumacy.lna (ZNPS).

Inną postać kanoniczną uzyskuje się w wyniku rozkładu funkcji logicznej na czynniki wg wzoru

f(x₁,x₂,...,x_n) = [x₁+f(0,x₂,...,x_n)][x₁+f('l,x₂.....x_a)]    (J.12)

Kontynuując ten rozkład i stosując w każdym kroku aksjomat (§) otrzymujemy ostatecznie

f(x₁,x₂,...,x_a) = £x₁+x₂+...+x_a+f(0,0,...,O>]|lć₁+x₂+...+x_o+f(1,0,..,g .]

..[x₁+x₂+.;.+x_n+f(1,1,...,i)]    (1.13)

Przyporządkowując każdej pełnej sumie liczbę binarną wg zasady*^

-0,    x_fc—^~1    (1.14)

możemy Ją (tzn. sumę) oznaczyć symbolem S^, gdzie i reprezentuje wartość dziesiętną uzyskanej liczby binarnej (numer sumy). Np. pełnej sumie x₁+x₂+ij odpowiada liczba (010)₂ = (2)_1Q, a więo oznaczamy Ją symbolem Sg. Wzór (1.13) można teraz zapisać w postaci

ż"-i

f(x_1tx₂,...,x_n) = n (^si + )• = n s.    (1.15)

i-o    a_t-o

Przedstawienie funkcji w postaci iloczynu pełnych sum, odpowiadających -zgodnie z przyporządkowaniem (1.14) - tym próbkom wartości zmiennych,przy których funkcja ta przyjmuje wartość 0, nazywamy zuoełna normalna postacią iloczynowa (ZNPI).

Przykład 1.21    .

Funkcję f = (x^    @ x₂) —— x₂Xj przedstawić w postaciach kanonicznych

*1*1		*s	*i«*:	*t‘y	(x,©*i)— 7,xy	I
1	1	1	i	0	1	8\
1	0	f	i	ł	l	6v
0	1	•	i	0	8	1'
I		ł	i	1	1	V
i	0	0	i	8	»
ł	8	1	i	«	1	1-
1	1	0	e	8	1	0'
1	1	1	e	1	1	8'

Rys. 1.20. Tablica funkcji z przykładu 1.21

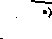
Zwróćmy uwagę,

1

że przyporządkowanie to jest odwrotne do (1.10).