Scan10046

l<x<2

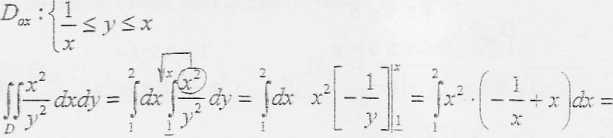
X

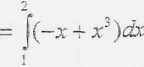
O

V m

j_L= 9

4~ 4

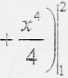
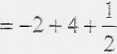
Zamiana zmiennych w całce podwójnej.

W niektórych przypadkach obliczenie całki podwójnej możemy uprościć wprowadzając nowe zmienne.

Niech f(x,y)- ciągła w regularnym obszarze D oraz x=q>(u,v)_/ y=y(u,v) są funkcjami ciągłymi wraz z pierwszymi pochodnymi w obszarze regularnym a i D jest obrazem A oraz tzw, jakobian olcfeśla-my:

J(u,v) =

dę	dę	j i
du	dv
dy/	dy.y
du	dv
	i	7(
	i D

jest =0, Wówczas:

jj/(x_fy)dxdy = JJf(<p(u, v), y/(u, v)) • |/| • duav

Najważniejszym typem zamiany zmiennych jest wprowadzenie tzw. współrzędnych biegunowych r, <p punktu P(x,y):

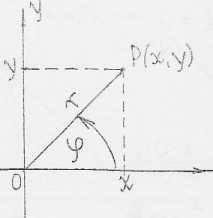
Wówczas:

i iiw—iiBfrrwi mimwiiiiiiiiio<ii(uf.

IX = 7" COS

I*

ty = rsinpl J = r

X