0000023(1)

GENETYKA

P:

G:

F.:

G:

gładkie, wysokie AAKK

AK

omszone, karłowate

aabb

gładkie, karłowate

P:    AAbb

omszone, wysokie j.i KK

a b

ttktdkic. wysokie

AaKb'

AK

, ab || Ab 0.47    0.47    0.0}

aK

0.03

■O	AK	ab	Ab	aK
0.47 Ali	AAKK 0,221	AaKb 0.221	AAKb 0.014	AaKK 0.014
0.47 ab	AaBb 0.221	aabb 0.221	Aabb 0.014	aaKb 0.014
0,03 Ab	AAKb 0,014	Aabb 0.014	AAbb 0.001	AaKb 0.001
0.03 .t#	AaKK 0.014	aabb 0.014	AaKb 0.001	aaKK 0.001

A_K_

Abb

d.itf

.uibb

72.1 % potomstwa 2.9% potomstwa 2.9% potomstwa 22.1% potomstwa

G:

G:

/U>

.i K

gładkie, wysokie AaKb

AI>

. d# II AK . 0.47    0.47    0.03

ab

0.03

n	Ab	aK	AK	ab
0.47 Ab	AAbb 0.221	AaKb 0.221	AAKb 0.014	Aabb 0.014
0.47 aK	AaKb 0.221	aaKK 0.221	AaKK 0.014	aaKb 0.014
0.03 AK	AAKb 0.014	AaKK 0,014	AAKK 0.001	AaKb 0.001
0.03 ab	Aabb 0.014	aaKb 0.014	AaKb 0.001	aabb 0.001

A_K_

Abb

aaB_

aabb

50,1% potomstwa 24.9% potomstwa 24.9% potomstwa 0.1% potomstwa

KRZYŻÓWKA TESTOWA

(zF,)/l.iMł x aabb

KRZYŻÓWKA TESTOWA (z Fj )AaKb X aabb

G:	AK .	ab ||	Ab .	aK	; ab	G:	Ab .	aB II	AK ,	ab	; ab
P =	0.47	0,47	0.03	0.03		P ■	0.47	0.47	0.03	0.03
	AK	ab	Ab	aK			Ab	aK	AK	ab
17 -	AaKb	aabb	Aabb	aaKb	n	*-v	Aabb	aaKb	AaKb	aabb	-3
^r2-	0.47	0.47	0.03	0.03	ab u		0.47	0.47	0.03	0.03	ab n
	47%	47%	3%	3%	—		47%	47%	3%	3%	—

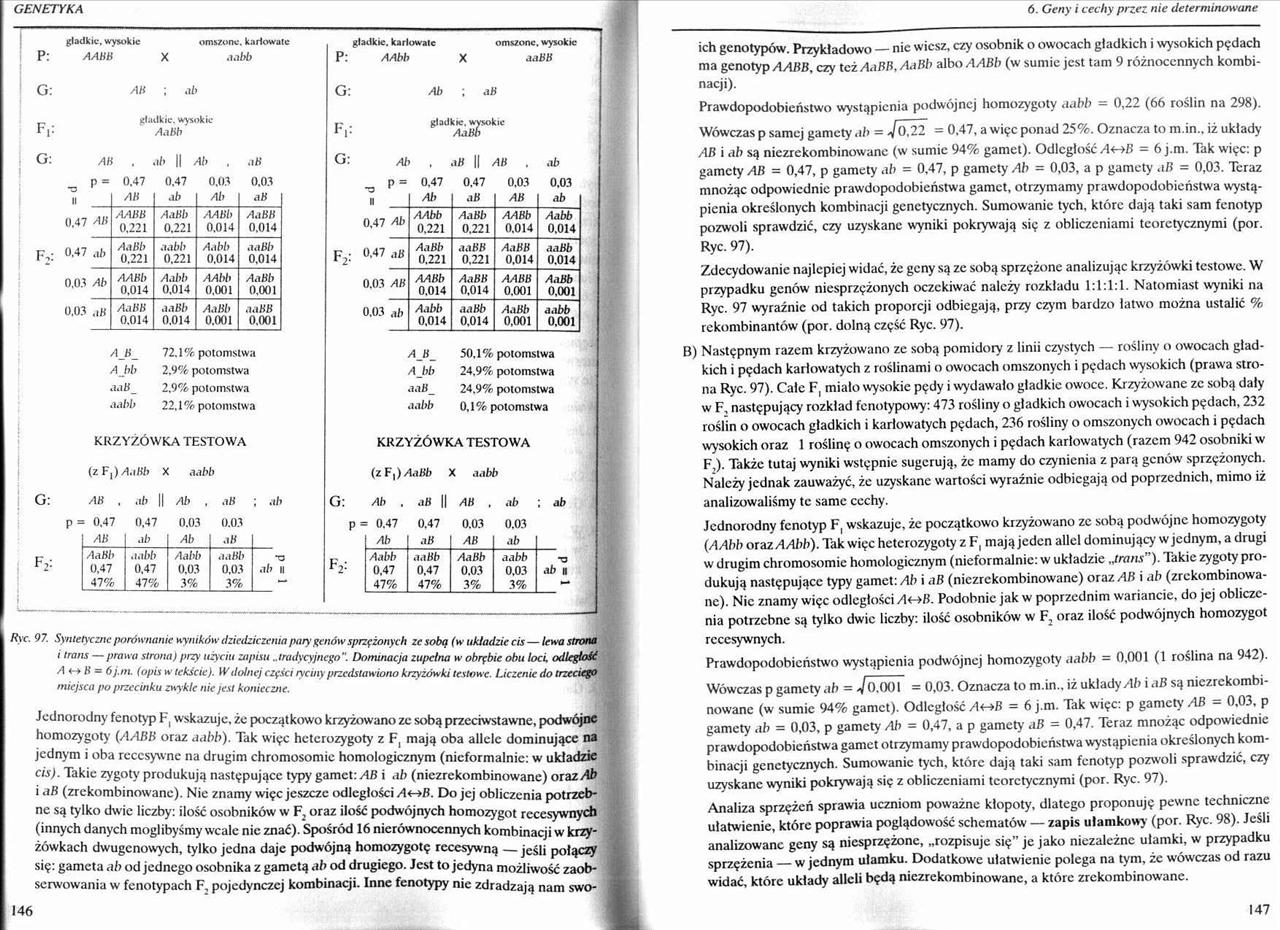
Ryc. 97. Syntetyczne porównanie wyników dziedziczenia pary genów sprzężonych ze sobą (w układzie cis — lewa strona i trans —prawa strona) przy użyciu zapisu ..tradycyjnego". Donunacja zupełna w obrębie obu lock odlegjlośŁ A < *K = 6j.m. (opis w tekście). W dolnej części ryciny przedstawiono krzyżówki testowe. Liczenie do trzeciego miejsca po przecinku zwykle nie jest konieczne.

Jednorodny fenotyp F, wskazuje, że początkowo krzyżowano ze sobą przeciwstawne, podwójne homozygoty (AABB oraz .uibb). Tak więc heterozygoty z F, mają oba alicie dominujące na jednym i oba rcccsywne na drugim chromosomie homologicznym (nieformalnie: w układzie cis). Takie zygoty produkują następujące typy gamet: AB i .i b (niezrekombinowane) oraz Ab i dB (zrekombinowane). Nie znamy więc jeszcze odległości Ac->B. Do jej obliczenia potrzeb ne są tylko dwie liczby: ilość osobników w F, oraz ilość podwójnych homozygot rcccsywnych (innych danych moglibyśmy wcale nic znać). Spośród 16 nierównoccnnych kombinacji w krzyżówkach dwugcnowych, tylko jedna daje podwójną homozygotę rcccsywną — jeśli połączy się: gameta db od jednego osobnika z gametą db od drugiego. Jest to jedyna możliwość zaobserwowania w fenotypach F, pojedynczej kombinacji. Inne fenotypy nie zdradzają nam swoich genotypów. Przykładowo — nic wiesz, czy osobnik o owocach gładkich i wysokich pędach ma genotyp AAKB, czy też AaBB,AdBb albo AABb (w sumie jest tam 9 różnoccnnych kombinacji).

Prawdopodobieństwo wystąpienia podwójnej homozygoty ddbb - 0,22 (66 roślin na 298).

Wówczas p samej gamety db = Jo.22 = 0.47, a więc ponad 25%. Oznacza to m.in.. iż układy AB i db są niczrckombinowanc (w sumie 94% gamet). Odległość/!<->/> = 6 j.m. Tak więc: p gamety AB = 0,47, p gamety db = 0,47, p gamety Ab = 0,03, a p gamety dB = 0,03. Teraz mnożąc odpowiednie prawdopodobieństwa gamet, otrzymamy prawdopodobieństwa wystąpienia określonych kombinacji genetycznych. Sumowanie tych. które dają taki sam fenotyp pozwoli sprawdzić, czy uzyskane wyniki pokrywają się z obliczeniami teoretycznymi (por. Ryc. 97).

Zdecydowanie najlepiej widać, że geny są ze sobą sprzężone analizując krzyżówki testowe. W przypadku genów niesprzężonych oczekiwać należy rozkładu 1:1:1:1. Natomiast wyniki na Ryc. 97 wyraźnie od takich proporcji odbiegają, przy czym bardzo łatwo można ustalić % rckombinantów (por. dolną część Ryc. 97).

B) Następnym razem krzyżowano ze sobą pomidory z linii czystych — rośliny o owocach gładkich i pędach karłowatych z roślinami o owocach omszonych i pędach wysokich (prawa strona Ryc. 97). Całe F, miało wysokie pędy i wydawało gładkie owoce. Krzyżowane ze sobą dały w F, następujący’ rozkład fenotypowy: 473 rośliny o gładkich owocach i wysokich pędach, 232 roślin o owocach gładkich i karłowatych pędach, 236 rośliny o omszonych owocach i pędach wysokich oraz 1 roślinę o owocach omszonych i pędach karłowatych (razem 942 osobniki w F,). Także tutaj wyniki wstępnie sugerują, że mamy do czynienia z parą genów sprzężonych. Należy jednak zauważyć, że uzyskane wartości wyraźnie odbiegają od poprzednich, mimo iż analizowaliśmy te same cechy.

Jednorodny fenotyp F, wskazuje, że początkowo krzyżowano ze sobą podwójne homozygoty (A Abb oraz A Abb). Tak więc heterozygoty z F, mają jeden allel dominujący w jednym, a drugi w drugim chromosomie homologicznym (nieformalnie: w układzie „trans’'). Takie zygoty produkują następujące typy gamet: Ab i dB (niezrekombinowane) oraz AB i ab (zrekombinowa-nc). Nic znamy więc odległości Podobnie jak w poprzednim wariancie, do jej obliczenia potrzebne są tylko dwie liczby: ilość osobników w F, oraz ilość podwójnych homozygot rcccsywnych.

Prawdopodobieństwo wystąpienia podwójnej homozygoty aabb = 0.001 (1 roślina na 942).

Wówczas p gamety ab = V0.001 = 0,03. Oznacza to m.in., iż układy Ab i aB są niczrckombinowanc (w sumie 94% gamet). Odległość A<->B = 6 j.m. Tik więc: p gamety AB = 0.03. p gamety ab = 0,03, p gamety /ti> = 0,47, a p gamet)’ aB = 0,47. Teraz mnożąc odpowiednie prawdopodobieństwa gamet otrzy mamy prawdopodobieństwa wystąpienia określonych kombinacji genetycznych. Sumowanie tych, które dają taki sam fenotyp pozwoli sprawdzić, czy uzyskane wyniki pokrywają się z obliczeniami teoretycznymi (por. Ryc. 97).

Analiza sprzężeń sprawia uczniom poważne kłopoty, dlatego proponuję pewne techniczne ułatwienie, które poprawia poglądowość schematów — zapis ułamkowy (por. Ryc. 98). Jeśli analizowane geny są niesprzężonc, „rozpisuje się” je jako niezależne ułamki, w przypadku sprzężenia — w jednym ułamku. Dodatkowe ułatwienie polega na tym, że wówczas od razu widać, które układy alleli będą niezrekombinowane, a które zrekombinowane.

147