062 3

Ciąg geometryczny

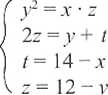
<- z równania x + f = 14 obliczamy t z równania y + z = 12 obliczamy z

y¹ = x • (12-y)

2 (12 - y) = y + (14 - x) t= 14-x z — 12-y

y² = 12x — xy 24-2y = y + \4-x t= 14-x

z = 12 —y

y- = \2x~xy -2y-y + x=\4-24 t= 14 - x z = 12 -y

y-= 12x-xy -3y + x = -10 /= 14-x z = 12 -y

y² = 12x -xv x = 3y -10 t= 14-x z= 12—y

y²- 12(3y- 10) — (3y — 10)y x = 3y - 10 t= 14-x z = 12-y

y² = 36y - 120 - 3r +10y x = 3y - 10 t= 14-x z= 12-y

y² - 36y +120 + 3y² - 10y = 0 x = 3y- 10 t= 14-x z = 12-y

<• • w miejsce z podstawiamy 12-y <- w miejsce t podstawiamy 14 - x

w miejsce x podstawiamy 3y- 10

to równanie trzeba uporządkować

62