105

Ciąg geometryczny nieskończony

Lewą stronę równania można zastąpić sumą

S =:

•, czyli

15| l+- + 4 + ...)= 15

x x^L )    i_2

, przy założeniu x e (-cc, -2) u (2, +oc)

x

Teraz zajmujemy się prawą stroną równania

, 11. ...

1 +    + — + ... jest to szereg geometryczny o ilorazie

i pierwszym wyrazie a_{ = 1 i x * 0

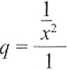
x²

Możemy znaleźć sumę tego ciągu, tylko pod warunkiem że

M<1

Czyli

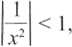
x ^ 0

Inaczej

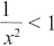
—■ przyjmuje tylko wartości dodatnie, zatemj też, dlatego moduł można opuścić.

x²

-KO

-#<0

x

x²( 1 - x²) < 0

x, = 0^(2>, x₂ = x₃ = 1">,

Zastępujemy iloraz iloczynem (badamy znak), znajdujemy pierwiastki i rysujemy pomocniczy wykres znaku nierówności.

„0" jest pierwiastkiem dwukrotnym, dlatego wykres odbije się od osi OX w tym punkcie (nie przetnie osi 0X w punkcie 0),

105