099

Ciąg geometryczny nieskończony

Zatem

x²-3x<0, gdy x e (0,3)    a=\,b = -3,c=2

X²- 3x + 2 > 0

A = (-3)^:-4 • 1 -2 = 9-8 = 1 va = i

_v ^{3 + 1 4}

Pomocniczy wykres

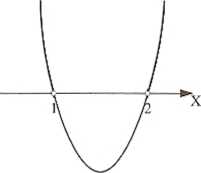
x e (—co, 1) (2, +co)

Zatem

x²- 3x + 2 > 0, gdy x e (-cc, 1) u (2, +x)

Ponieważ rozwiązujemy układ nierówności, należy znaleźć część wspólną podkreślonych zbiorów

x s (0, 3)

x 6 (-00, 1)					x e (2, +oc)
—	—	—	»-	—	^1-

0    12    3

xe (0, 1) u (2, 3)

Zatem

\q\ < 1, gdy x e (0, l)u(2, 3)

99