104 2

Ciąg geometryczny nieskończony

X		Korzystamy z twierdzenia < o W(x) ■ P(w) < 0 i P(x) * 0 I (Xy
l^2r>°		gdzie W(x) i P(x) to dowolne wielomiany
j x(2 - x) < 0 | x(2 +x)>0
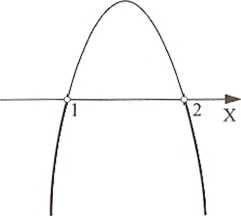
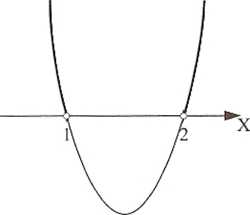
x(2~x)<0	oraz	x(2 + x) > 0
xt = 0, x2 = 2		II O II I K)

R_t: x e (-co, 1) u (2, +oc)    i    R,: x e (-x, -2) u (0, +oo)

Teraz część wspólna zbiorów R₍ i R,

	-1-	>-1-<	—	—►

-2 0 2

x e (-20, -2) u (2, +co)

Czyli

\q\ < 1, gdy x e (-co, -2) u (2, +co)

104