1tom008

1. WYBRANE ZAGADNIENIA Z MATEMATYKI I FIZYKI 18

— iloczyn

zi£j = (x₁x₂-y₁y₂, x₁y₂ + x₂y₁)

— iloraz

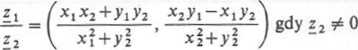
Stąd wynika równość j² = — 1.

Liczbą sprzężoną z liczbą z = (x, y) jest nazywana para z* = (x, — y). Na płaszczyźnie z prostokątnym układem kartezjańskim Oxy liczbie zespolonej odpowiada wektor

OP = (x, y). Osie Ox i Oy są nazywane opowiednio osią rzeczywistą i osią urojoną, a płaszczyzna Oxy — płaszczyzną zespoloną.

Liczbę zespoloną można zapisać w następujących postaciach:

1.    Postać kartezjańska

z = x+jy; z*=x-jy

2.    Postać trygonometryczna

z = r (cos cp + j sin cp);    z* = r (cos cp — j sin (p)

w której r = |z| = _s/x¹+y¹ nazwano modułem liczby zespolonej, równym długości wektora OP. _

Jeżeli z # 0, to miarę łukową <p, kąta skierowanego od osi Ox do wektora OP, nazywa się argumentem liczby zespolonej i oznacza

Arg z = ę

przy czym: cos cp = x/r, sin <p = y/r.

Jeżeli — u < cp ^ %, to liczba ta jest nazywana argumentem głównym.

3.    Postać wykładnicza

z = re^iv; z* = re^-'*

Liczba zespolona e?⁹ jest nazywana operatorem obrotu o kąt cp.

Często korzysta się z następujących wzorów i równości:

— wzory Eulera

sin<p = — (e*—e ‘⁹)

—    wzór Moivre’a

(cos cp + j sin cp)" = cos n cp + j sin n cp

—    potęga liczby zespolonej

z" = r"(cosnę)+jsinnę)) = rⁿeⁱⁿ⁹

—    pierwiastek n-tego stopnia liczby zespolonej

<p+2kn . . cp+2kn

--hj sin-

n    n

dla k = 0,1,...,(« — !)

przy czym n — liczba naturalna. Stąd wynika, że wj = z;

p_rZy k = O pierwiastek n-tego stopnia z liczby zespolonej z jest nazywany pierwiastkiem głównym',

_ logarytm liczby zespolonej jest funkcją okresową o okresie urojonym równym 2knj

i wdraża się wzorem

ln z = lnr+j(<p+2/cre) dla k = 0,1,...

gdzie lnr — logarytm naturalny z modułu liczby z.

Dla k = 0 otrzymuje się wartość główną logarytmu

ln z = Inr+ję)

W przypadku liczb zespolonych ze sobą sprzężonych zachodzą następujące równości: zz* = |z|²;    |z*| = |z|; Arg z* = - Argz;

(£i ±z₂)* = zf ±zf; (£i£z)* = £*£*;

(z")* = (z*)";    (£i/£₂)* = £*/£?;    [</lT = </i*;

oraz

l£i£zl = l£ill£zl; Arg(z₁-z₂) = Argz,+Argz₂

Pierwiastki wielomianu

Liczba z₀ jest pierwiastkiem wielomianu W(z), jeżeli wielomian ten jest podzielny przez

(z-£o)-

Jeżeli wielomian

W(i) = a_nz’+a_n__lz"~¹ +...+a₀

jest stopnia n, to istnieje n liczb zespolonych z„...,z„, w których każda z nich jest pierwiastkiem wielomianu. Wówczas

^w(l) = ^a„(£—£i) •••(£-£„)

Liczba z₀ jest k-krotnym pierwiastkiem wielomianu W(z), jeżeli W(z) = (z-z₀)*G(z)

gdzie G (z) jest wielomianem stopnia (n—k) oraz G(z₀) # 0.

Wielomianem rzeczywistym jest nazywany wielomian W (z), w którym współczynniki dla k = 0.1. ...,n są liczbami rzeczywistymi. Jeżeli liczba z₀ jest pierwiastkiem zespolonym wielomianu rzeczywistego, to liczba z? z nią sprzężona jest także pierwiastkiem tego wielomianu i oba pierwiastki mają tę samą krotność.

Przy badaniu stabilności ruchu korzysta się z twierdzenia Hurwitza: warunkiem koniecznym i wystarczającym na to, aby wszystkie pierwiastki wielomianu rzeczywistego postaci

W(z) = a„z" + ... + a₀, n > 1, a„ > 0

miały części rzeczywiste ujemne jest, żeby był spełniony układ n nierówności zapisany za pomocą wyznaczników (patrz p. 1.2.2)

>0, |^a'¹"^{1 a}"    I > 0,

I —3    — 2 I

2*