1tom024

1. WYBRANE ZAGADNIENIA Z MATEMATYKI I FIZYKI 50

Pracę W wykonaną przy przemieszczaniu iadunku można wyrazić wzorem W= -qAV=q(V_A-V_B)    (1.24)

gdzie różnica potencjałów AV = V_B—V_A nazywa się napięciem między punktem B i punktem A pola elektrostatycznego.

Między potencjałem V(r) w danym punkcie pola i jego natężeniem E(T) w tym punkcie, zachodzi związek

£(r) =-grad F(r)    (1.25)

co oznacza, że wektor natężenia pola jest skierowany wzdłuż kierunku najszybszego spadku potencjału i ma wartość równą spadkowi potencjału na jednostkę odległości w tym kierunku.

Potencjał pola elektrostatycznego jest addytywny, tzn., że w przypadku nakładania się pól elektrostatycznych ich potencjały sumują się algebraicznie.

Pojemność elektryczna C odosobnionego przewodnika jest to stosunek umieszczonego na nim ładunku q do potencjału V, jaki skutkiem tego uzyskuje ten przewodnik

C = q/V    (1.26)

Pojemność zależy od kształtu oraz wymiarów przewodnika i jest wprost proporcjonalna do przenikalności elektrycznej bezwzględnej ośrodka, w którym znajduje się przewodnik. Na przykład pojemność elektryczna izolowanej kuli o promieniu R wynosi

C = 4ne₀e_rR    (1.27)

Pojemność elektryczna wzajemna dwóch przewodników (np. kondensatora) jest to stosunek ładunku q przeniesionego z pierwszego przewodnika na drugi do różnicy potencjałów (V₂ — Vy) jaka skutkiem tego pojawi się między nimi

C =

g

yi-y,

(1.28)

Pojemność wzajemna zależy od kształtów, wymiarów i wzajemnego położenia przewodników, a także od przenikalności dielektrycznej e ośrodka, w którym się one znajdują.

Energię dowolnego układu ładunków w próżni lub dielektryku izotropowym (a, > 1) można przedstawić w postaci

E_e = \je₀s,E²dV    (1.29)

ly

_ Gęstość objętościowa energii pola elektrycznego w ośrodkach izotropowych (D = e₀e_rE) jest określona zależnością

<>K

i^s°^e'^E

2

(1.30)

1.3.3. Prąd stały

Prądem przez powierzchnię S jest nazywana wielkość skalarna i równa pierwszej pochodnej względem czasu ładunku q przepływającego przez tę powierzchnię

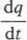
Gęstość prądu j jest wektorem zwróconym w kierunku ruchu ładunków dodatnich, o wartości

j =

di

dS⁷

(1.32)

gdzie: dS' — rzut elementu dS na płaszczyznę prostopadłą do j; di — prąd płynący przez

Gęstość prądu w przewodniku wyraża się przez koncentrację n swobodnych elektronów w przewodniku oraz ich prędkości ~v_k wzorem

T = <7* £    = ^n<łeVu

(1.33)

gdzie: q_e = — e — ładunek nośników prądu (swobodnych elektronów); v_u — prędkości unoszenia nośników prądu

(1.34)

Prawo Ohma: Wartość prądu stałego płynącego przez przewodnik jest wprost proporcjonalna do napięcia elektryczego U między końcami odcinka, a odwrotnie proporcjonalna do jego rezystancji R

U

(1.35)

Rezystancja przewodnika o stałej powierzchni przekroju poprzecznego S i długości /

(1.36)

gdzie q — rezystywność materiału przewodnika.

Prawo Ohma można również wyrazić przez gęstość prądu: Gęstość prądu w przewodniku jest równa iloczynowi konduktywności y = I/q przewodnika i natężenia poła elektrycznego E w przewodniku

(1.37)

Konduktywność całkowita półprzewodnika jest sumą jego konduktywności elektronowej (typu n) i dziurowej (typu p)

'I = e(nu„+pu_p)

(1.38)

gdzie: e — wartość bezwzględna ładunku nośnika prądu, tj. swobodnego elektronu lub swobodnej dziury (ładunek elementarny); n.p — koncentracje odpowiednio swobodnych elektronów i swobodnych dziur; u_n,u_p— ruchliwości odpowiednio elektronów i dziur, tj. ich średnie prędkości pod działaniem jednostkowego pola elektrycznego.

Koncentracje nośników prądu w półprzewodnikach zależą od temperatury T półprzewodników i są określone następująco:

dla półprzewodników samoistnych, tj. takich, dla których wpływ domieszek jest zaniedbywalny

n = p = AT^3/2e~^E,,2kT

(1.39)

gdzie: A — stała materiałowa; E_g — szerokość przerwy energetycznej między pasmem walencyjnym a pasmem przewodnictwa; k — stała Boltzmanna.

— dla półprzewodników domieszkowych (przy zaniedbaniu nośników samoistnych)

n = A_nJŃ~ T^VĄe~^E‘^,2kT

p=a„jń;t^-w"

•3/4_e-£₀/2lcT

(1.40)

(1-41)

gdzie: A„,A_p — stałe materiałowe odpowiednio dla elektronów i dziur, N_d,N_a

—    koncentracje odpowiednio donorów i akceptorów w półprzewodniku; E_d, E_c

—    energie jonizacji odpowiednio donorów i akceptorów.

Siła elektromotoryczna (sem) E jest różnicą potencjałów wytwarzaną przez źródło prądu. Przy braku prądu w źródle, jego sem jest równa napięciu na jego zaciskach.

4*