1tom027

1. WYBRANE ZAGADNIENIA Z MATEMATYKI I FIZYKI

gdzie d<P_m — elementarny strumień magnetyczny przez powierzchnię zakreśloną przez element dl poruszającego się przewodnika.

Praca wykonana podczas dowolnego przemieszczenia obwodu zamkniętego z prądem / = const

W= ZA<Z>,

m

(1.71)

przy czym A4>_m — zmiana strumienia magnetycznego przez powierzchnię rozpiętą na obwodzie, wywołana jego przemieszczeniem.

1.3.5. Indukcja elektromagnetyczna

Zjawisko indukcji elektromagnetycznej polega na powstawaniu siły elektromotorycznej (sem) indukcji e_f w obwodzie elektrycznym, na skutek zmian strumienia magnetycznego, przenikającego powierzchnię rozpiętą na tym obwodzie.

Prawo Faradaya indukcji elektromagnetycznej: Sem indukcji elektromagnetycznej e, jest równa, wziętej z ujemnym znakiem, szybkości zmian strumienia magnetycznego <l>_m skojarzonego z powierzchnią rozpiętą na tym obwodzie

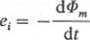
Znak minus jest wyrazem działania reguły Lcnza.

Reguła Lenza: Prąd indukowany w obwodzie ma zawsze taki kierunek, ze wytworzony przezeń strumień magnetyczny przeciwdziała tym zmianom strumienia zewnętrznego, które ten prąd wywołały.

Zjawisko samoindukcji polega na powstawaniu w obwodzie prądu zmiennego dodatkowej sem e_si wywołanej zmianą prądu płynącego w tym obwodzie. Siłę elektromotoryczną indukcji własnej można określić jako gdzie 4>_mc — własny strumień magnetyczny obwodu z prądem

(1.74)

s

Jest to strumień indukcji B_c pola magnetycznego wytworzonego przez prąd płynący w obwodzie, a przenikający powierzchnię S ograniczoną tym obwodem.

Jeżeli obwód znajduje się w ośrodku nieferromagnetycznym, to

(1.75)

gdzie: 1 — prąd w obwodzie; L — indukcyjność obwodu zależna od kształtu geometrycznego i wymiarów obwodu oraz od przenikalności magnetycznej ośrodka otaczającego obwód. Wówczas

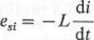
(1.76)

Zjawisko indukcji wzajemnej polega na wzbudzaniu sem e_w w obwodzie znajdującym się w sąsiedztwie innych obwodów, w których płyną prądy zmienne. Siła elektromotoryczna indukcji wzajemnej indukowana w obwodzie Zc-tym przez prąd zmienny płynący w obwodzie Z-tym jest wyrażona wzorem

(1.77)

gdzie M_u — indukcyjność wzajemna obwodu Ze-tego względem obwodu Z-tego.

W ośrodku nieferromagnetycznym M_kl = M_lk i zależy tylko od kszałtów geometrycznych, wymiarów oraz położenia wzajemnego obwodów, a także od względnej przenikalno-ści magnetycznej ośrodka, w którym znajdują się obwody. W tym przypadku

e. =    d-⁷⁸)

W ośrodku ferromagnetycznym natomiast M_u i M_lk zależą nie tylko od wielkości wymienionych wyżej, lecz również od wartości i zmian w czasie prądów i_k i i, płynących w obwodach.

Energia pola magnetycznego cewki E_m o indukcyjności L, umieszczonej w ośrodku nieferromagnetycznym jest wyrażona wzorem

£_m = iz./²    (1.79)

przy czym / — prąd płynący w cewce.

Objętościową gęstość energii pola magnetycznego w ośrodku nieferromagnetycznym można wyrazić zależnością

B²

co

m

2/<₀/V

(1.80)

w której: B — indukcja; p_r — względna przenikalność magnetyczna.

1.3.6. Równania Maxwella, fale elektromagnetyczne

Zmienne w czasie pole elektryczne zawsze wytwarza pole magnetyczne i na odwrót. Dlatego takie nierozłącznie powiązane ze sobą, zmienne w czasie pola: elektryczne i magnetyczne są traktowane jako jedno pok elektromagnetyczne, opisywane przez zmienne w czasie wektory elektryczne: £(F, t) i D (F, t) = e₀s_rE oraz wektory magnetycz

ne: B (r,t) i H(r,t) = B/p₀p_r.

Równania Maxwella są matematyczną podstawą klasycznej teorii pola elektromagnetycznego.

Postać całkowa

f £ d/ = -f

K    S

fDdS = Q

s

$B-dS =0

a		Postać różniczkowa
r cD	_¥	— SD —
—	•dS	rot H = — +j
s St		dt
cB	,	SB
-•	d S	rot£ —--—
5t		dt
		div D — q
		div B = 0

(1.81)

s

W postaci całkowej pierwszego i drugiego równania, S jest powierzchnią rozpiętą na zamkniętym konturze całkowania K, zaś i — wartością prądu przepływającego przez powierzchnię S. W trzecim i czwartym równaniu, S jest zamkniętą powierzchnią całkowania. Pozostałe symbole zachowują poprzednie znaczenia.

Pierwsze równanie Maxwella jest uogólnieniem prawa Ampere’a (p. wzór (1.67) i (1.67a)) uwzględniającym to, że wirowe pole magnetyczne powstaje nie tylko w wyniku ruchu ładunków elektrycznych (prądów), lecz również w wyniku zmian w czasie pola elektrycznego.

Drugie równanie — to rozszerzone prawo indukcji Faradaya (p. wzór (1.72)), opisujące zależność wirowego pola elektrycznego w dowolnym ośrodku od szybkości zmian w czasie pola magnetycznego.