1tom026

1. WYBRANE ZAGADNIENIA Z MATEMATYKI I FIZYKI

Natężenie pola magnetycznego H jest wielkością charakteryzującą pole magnetyczne, zdefiniowaną wzorem

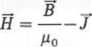
(1.58)

(1.59)

Dla substancji magnetycznie izotropowych zachodzi związek B = p₀g_rH

gdzie /i₀ = 4n-10 ⁷ H/m — przcnikalność magnetyczna próżni; p_r — względna przenikal-ność magnetyczna substancji wskazująca, ile razy, przy danym rozkładzie prądów makroskopowych, indukcja magnetyczna w danej substancji wypełniającej całą przestrzeń, jest większa niż w próżni.

Dla magnetyków znajdujących się w niezbyt silnych polach magnetycznych polaryzacja magnetyczna

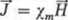
(1.60)

przy czym y_m — podatność magnetyczna.

Po uwzględnieniu wzorów (1.58) i (1.59) można napisać X_m = Pr-l

(1.61)

Podatność magnetyczna diamagnetyków y_m < 0 i (poza nadprzewodnikami, których X_m = “ 1) l/J jest rzędu 1(T⁵.

Dla paramagnetyków y_m > 0 i jest rzędu 10 ⁵.

W przypadku ferromagnetyków y zależy od natężenia pola magnetycznego oraz od przebiegu magnesowania (zjawisko histerezy) i może osiągać wartości rzędu 10⁴-f10⁵. Każdy ferromagnetyk powyżej charakterystycznej dla niego temperatury Curie T_c traci właściwości ferromagnetyczne i staje się paramagnetykiem.

__ Prawo Biota-Sacarta określa w ustalonym punkcie P indukcję pola magnetycznego dB pochodzącą od elementu przewodnika d/, przez który płynie prąd I (rys. 1.3) gdzie r — wektor skierowany od elementu dl do punktu P.

Indukcja pola magnetycznego pochodząca od całego przewodnika ma postać

B = JdB

L

(1.63)

przy czym_całka krzywoliniowa rozciąga się na cały rozważany przewodnik L.

Siła dF₁₂ oddziaływania magnetycznego elementu dl, przewodnika z prądem /, na element dl₂ przewodnika z prądem I₂, zgodnie ze wzorami (1.50) i (1.62), wynosi

dl, x(d7^ xr,₂)

(1.64)

gdzie T₁₂ — wektor poprowadzony odelemcntu dl, do elementu dl₂. Wektory dl, i dl₂ są określone analogicznie do wektora dl we wzorze (1.50).

Przy dwóch długich, prostoliniowych i równoległych przewodnikach z prądami /, i I₂, umieszczonych w próżni w odległości d od siebie, wartość siły F, działającej między jednym przewodnikiem a odcinkiem 1 drugiego przewodnika wynosi

Przewodniki z prądami płynącymi w kierunkach zgodnych przyciągają się, a z prądami o kierunkach przeciwnych — odpychają się.

Wzór (1.65) służy do definiowania jednostki prądu — ampera.

Cyrkulacją £ wektora indukcji pola magnetycznego B po konturze zamkniętym K nazywa się całkę

£_m = fBdł    (1.66)

K

gdzie d7~ — elementarny wektor styczny do konturu K o długości elementu di konturu, zwrócony w kierunku drogi całkowania.

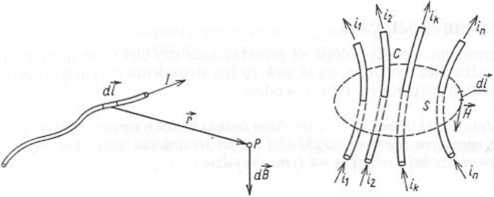
Rys. 1.3. Ilustracja prawa Biota-Savarta

Rys. 1.4. Ilustracja prawa Ampere’a

Prawo Ampere'a (prawo przepływu prądów): Cyrkulacja, po konturze zamkniętym K, wektora indukcji pola magnetycznego, wytworzonego przez stale prądy elektryczne, jest proporcjonalna do sumy algebraicznej prądów przepływających przez powierzchnię S rozpiętą na tym konturze (rys. 1.4). A zatem

= PoPr Z h    U-⁶⁷)

k = 1

gdzie n — liczba wszystkich przewodników z prądami objętych przez kontur K.

Prądy uważa się za dodatnie, jeśli ich zwrot jest związany regułą śruby prawoskrętnej z kierunkiem drogi całkowania.

Powyższe prawo można zapisać również w postaci różniczkowej

rot B = p₀p_r Z I_k    (^L67a)

i

Obwodem magnetycznym nazywa się ogół ciał lub obszarów przestrzeni, w których jest skupione pole magnetyczne.

Prawo Ohma dla zamkniętego obwodu magnetycznego (wzór Hopkinsonów) ma postać IN

#„ = — (1.68)

gdzie: <P_m — strumień magnetyczny przez poprzeczny przekrój obwodu (stały wzdłuż wszystkich odcinków obwodu): N — liczba zwojów cewki, przez krórą płynie prąd magnesujący I;R_m — całkowita reluktancja (oporność magnetyczna) obwodu.

Reluktancja odcinka obwodu magnetycznego o długości / i stałym polu S przekroju poprzecznego

R_ =

/

(1.69)

Po PrS

gdzie p_r — względna przenikalność magnetyczna danego odcinka obwodu magnetycznego.

Praca elementarna wykonywana przez siłę elektrodynamiczną podczas przemieszczania się elementu dl przewodnika z prądem / w polu magnetycznym

dW= /d<ż>

(1.70)