1tom028

1. WYBRANE ZAGADNIENIA Z MATEMATYKI I FIZYKI 58

Trzecie i czwarte równania — to prawa Gaussa odpowiednio dla pola elektrycznego i magnetycznego.

W przestrzeni wolnej od ładunków i prądów, równania Maxwella prowadzą po prostych przekształceniach do klasycznego równania falowego opisującego falę elektromagnetyczną

d²W(r,t) AW= e_oe_rg₀g_r——₂—

(1.82)

gdzie: A — operator Laplace’a, a W reprezentuje E, B, D lub II. Oznacza to, że pole elektromagnetyczne może istnieć w postaci fali, zwanej falą elektromagnetyczną, rozchodzącą się z prędkością

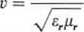
gdzie c = (ł'oMo)~^1/2 ~ 3- 18^s m/s — prędkość światła w próżni.

Doświadczalnie — jako pierwszy — fale elektromagnetyczne odkrył Hertz.

Teoria i doświadczenie zgodnie pokazały, że fale elektromagnetyczne można scharakteryzować następująco: _ _

— są falami poprzecznymi, przy czym wektory E i H są wzajemnie prostopadłe i leżą w płaszczyźnie prostopadłej do wektora prędkości fali v.

— przenoszą energię; wartość i kierunek chwilowej gęstości strumienia tej energii określa wektor Poyntinga

Ś = ExH (1.84)

(1.85)

-— przenoszą pęd, który w przestrzeni jest rozłożony z gęstością objętościową _ ExH S

— w zależności od długości fali /. są dzielone (z grubsza) na: fale radiowe (/. > 10 ” ⁴ m), fale świetlne (5- 10“⁴m > X> 10“⁹ m), promienie Roentgena (2- 10^_9m > ). > 6-10“¹⁰ m) ^promienie y (10~¹⁰ m > /. > 10“¹³ m).

Źródłami fal elektromagnetycznych są ładunki elektryczne poruszające się ruchem niejednostajnym lub nieprostoliniowym. Najczęściej spotykanymi są fale elektromagnetyczne wysyłane przez drgające dipole elektryczne (makroskopowe, czyli obwody elektryczne, i mikroskopowe, czyli układy atomowe i jądrowe).

LITERATURA

1.1. Astachow A. W., Szirokow J. M.: Kurs fizyki. Tom 2. Warszawa, WNT 1990.

1.2. Fortuna U., Macukow B., Wąsowski J.: Metody numeryczne. Warszawa, WNT 1995.

1.3. Hering M.: Termokinetyka dla elektryków. Warszawa, WNT 1980.

1.4. Kaczmarek Z.: Metody statystyczne w hydrologii i meteorologii. Warszawa, WKiŁ 1970.

1.5. Kaczorek T.: Teoria sterowania. Warszawa, PWN 1977.

1.6. Kącki R.: Równania różniczkowe cząstkowe w zagadnieniach fizyki i techniki. Warszawa, WNT 1995.

1.7. Orear Jay: Fizyka. Tom 1. Warszawa, WNT 1995.

1.8. Osiowski J.: Zarys rachunku operatorowego. Warszawa, WNT 1981.

1.9. Papoulis A.: Obwody i układy. Warszawa, WKiŁ 1988.

1.10. Plucińska A., Pluciński E.: Elementy probabilistyki. Warszawa, PWN 1981.

1.11. Poradnik inżyniera. Matematyka. Tom 1 i 2. Warszawa, WNT 1986.

1.12. Purcell E.M.: Elektryczność i magnetyzm. Warszawa, PWN 1974.

Rysunek techniczny elektryczny_Z^~7

mgr ini. Tadeusz Sapiński

2.1. Wiadomości ogólne

Elementami głównymi rysunków technicznych elektrycznych są oznaczenia i symbole graficzne elektryczne.

Rysunki takie można podzielić na schematy i diagramy. Do schematów są zaliczane często tablice (tabele) i wykazy (karty), natomiast do diagramów — wykresy.

Schematy elektryczne można podzielić na cztery grupy: podstawowe, wyjaśniające, wykonawcze i plany. Wśród schematów podstawowych rozróżnia się: schematy strukturalne i funkcjonalne, wśród schematów wyjaśniających — schematy zasadnicze i zastępcze, wśród schematów wykonawczych — schematy połączeń wewnętrznych, połączeń zewnętrznych i przyłączeń, wśród planów — plany rozmieszczenia instalacji, sieci oraz linii elektrycznych (PN-79/E-01244 [2.5]).

W zależności od złożoności merytorycznej obiektu elektrycznego^{1 2} stosuje się wszystkie rodzaje schematów bądź niektóre, bądź wydzielone ich części.

Rozróżnia się następujące oznaczenia: literowe wielkości fizycznych, alfanumeryczne (literowo-cyfrowe, literowe, cyfrowe), kodowe i barwne.

Symbole graficzne elektryczne dzieli się na: ogólne, przedmiotowe i rozróżniające. Symbole ogólne określają zjawiska występujące w elektryce, symbole przedmiotowe przedstawiają obiekty elektryczne, symbole rozróżniające określają zasady pracy obiektów, rodzaj wykorzystywanego zjawiska lub jego właściwości (PN-92...93/E-01200/01...13 [2.2]; PN-89/E-01215 [2.3]). W podanej literaturze normy do obowiązkowego stosowania w Polsce wyróżniono drukiem półgrubym.

Źródłem informacji o znormalizowanych oznaczeniach i symbolach graficznych są normy polskie ustanawiane przez Polski Komitet Normalizacyjny, w skrócie PKN (uprzednio Polski Komitet Normalizacji Miar i Jakości, w skrócie PKNMiJ). Nazwa i jej skrót obowiązują w Polsce od 01.01.1994 r. (Dz.U. nr 55, poz. 251).

Rysunki techniczne elektryczne wykonane zgodnie z wytycznymi norm międzynarodowych stają się zrozumiałe na całym świecie i często zawierają niezbędne informacje dotyczące obiektów i wyrobów elektrycznych. Zagadnienia związane z rysunkami technicznymi elektrycznymi obszernie omówiono w książce: K. Michel, T. Sapiński s,Rysunek techniczny elektryczny”, Warszawa, WNT 1987.

Obiektem może być: wyrób, instalacja, zespół lub pojedyncze urządzenie, maszyna, aparat lub jego element

(część).