203(1)

934. Obliczyć pochodną kierunkową funkcji u - x¹Ą-y² w punkcie

*4(3,4):

1)    w kierunku dwusiecznej pierwszego kąta układu współrzędnych,

2)    w kierunku promienia wodzącego punktu A,

3)    w kierunku wektora q[4, —3].

Rozwiązanie. Wyznaczamy pochodne cząstkowe funkcji u i obliczamy ich wartości w punkcie A

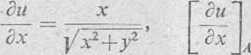
3

5

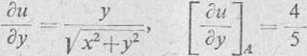
Podstawiamy obliczone wartości pochodnych do wzoru (a). Otrzymamy wtedy wyrażenie na pochodną funkcji u w punkcie A w dowolnym kierunku /[cosa, cos/?]

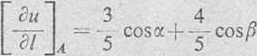
Z kolei znajdujemy cosinusy kątów a i fi, jakie dane kierunki różnicz->wania tworzą z osiami układu i obliczamy pochodne funkcji u w tych erunkach. Mamy

1) dla dwusiecznej pierwszego kąta układu współrzędnych a = /? — 45°_?

8ul ₌ J3_    j/2' , _4_    j/2

81, ]_A ~ 5 ' ' 2 ^T 5    2    10

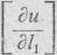
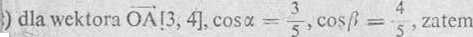
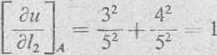
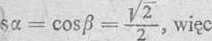
4    3    I iu I

’la wektora #[4, —3], cosa = y, cos/? = - y, czyli    = 0 5. Wyznaczyć pochodną kierunkową funkcji u — xy yz \ \ w kie-u wektora /[12, —3, —4] w punkcie dowolnym i w punktach —2, —1) oraz B(3, 3, 5).

Rozwiązanie. Znajdujemy pochodne cząstkowe funkcji u i cosinusy

k erunkowe wektora /

u_x ™ y, Uy \-\~z, u_x --- y

12    ³    4

cosa=—, cosp = —jy, cosy — ——

Podstawiając obliczone wartości do wzoru (a) znajdujemy pochodną funkcji u w kierunku l w dowolnym punkcie

, 12

^w' = it y-

A-_(x+z)_±_y= *y~

13 ^ ^{1 ;}    13 '    13

Z kolei podstawiając współrzędne punktów A i B, otrzymamy

u\(A)=-1,    u\(B) = 0

936. Jaka jest największa prędkość wzrastania funkcji «(M) = ^

kiedy punkt M(x, y, z) zbliża się do punktu M₀(— 1, 2, —2)? W jakim kierunku powinien poruszać się punkt M przy zbliżaniu się do punktu -kij(2, 0, 1), aby funkcja u(M) malała przy tym z największą prędkością?

Rozwiązanie. Największa co do wartości bezwzględnej prędkość zmian (wzrastania lub malenia) funkcji u(M) przy zbliżaniu się punktu M do ustalonego punktu P liczbowo jest równa modułowi gradient-.; funkcji w punkcie P. Funkcja będzie przy tym wzrastać albo maleć z największą prędkością w zależności od tego, czy punkt Af przy zbliżaniu się do punktu P porusza się w kierunku gradientu funkcji w punkcie P, czy też w kierunku przeciwnym.

Pamiętając o tym, obliczamy pochodne cząstkowe funkcji u oraz ze w'zoru (b) wyznaczamy gradient funkcji w dowolnym punkcie

20

^grad" = " ^(xi+yJ+zk)

Z kolei znajdujemy:

1) grad u(M₀) = y (i—2jj~2k); jego moduł równy liczbowo szukanej

największej prędkości wzrastania funkcji u(M) przy zdążaniu punktu M do Mo, wynosi

3

5

[grad u(M_q)\ = |/(y) +(~) +(y)

2) grad u(M() = — -y- i - k;

409 i