8 (17)

143

Zadania

14. Niech/ będzie ciągłą funkcją rzeczywistą określoną na R' mającą własności: 0 ^/(r) < l,/(f+2) =/(t)dla dowolnego r i

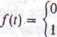
dla 0 « t « 1/3, dla 2/3 < r < 1.

Określmy <P(t) = (x(r), y(t)), gdzie

*(')= I 2-/(3²”-‘r),    y(r)= £ 2-’/<3^J"r).

Udowodnić, że # jest ciągła i że <P odwzorowuje I — <0, 1> na kwadrat jednostkowy /² c R⁷. Pokazać, że w istocie <P odwzorowuje zbiór Cantora na l².

Wskazówka. Dowolny punkt (x₀, y₀) e /² ma postać

łl« 1

J'0 = Z

gdzie każda z liczb a, jest równa 0 łub 1. Jeżeli to pokazać, że/(3*t₀) = a», a zatem x(t₀) = x₀, y(t₀) = y₀-

(Ten prosty przykład, tak zwanej „krzywej wypełniającej przestrzeń”, podał I. J. Schoenberg, Buli. A. M. S. voL 44,1938, str. 519.)

15.    Przypuśćmy, że/ jest funkcją rzeczywistą określoną na R‘,/,(t) = f{nt) dla n — tf; 2) 3,... i ciąg/, jest jednakowo ciągły na <0,1>. Co wynika stąd na temat/?

16.    Niech {/„} będzie ciągiem funkcji jednakowo ciągłych określonych na zwartym zbiorze K i niech {/,} będzie punktowo zbieżny na K. Wykazać, że ciąg ten jest na K zbieżny jednostajnie.

17.    Zdefiniować pojęcia jednostajnej zbieżności i jednakowej ciągłości dla odwzorowań o wartościach w dowolnej przestrzeni metrycznej. Pokazać, że twierdzenia 7.9 i 7.12 pozostają i w tym przypadku prawdziwe, twierdzenia 7.8 i 7.11 pozostają prawdziwe w przypadku odwzorowań w dowolną przestrzeń metryczną zupełną, a twierdzenia 7.10,7.16,7.17,7.24 i 7.25 są prawdziwe dla funkcji o wartościach wektorowych, tj. dla odwzorowań w dowolną przestrzeń R^k.

18.    Niech ciąg {/,} będzie jednostajnie ograniczony, a funkcje /, niech będą całkowalne w sensie Riemanna na <a, b). Określmy

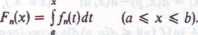
Udowodnić, że istnieje podciąg {F,J zbieżny jednostajnie na <a, b}.

19.    Niech K będzie zwartą przestrzenią metryczną. Niech S będzie podzbiorem 'if(AC). Wykazać, że S jest zwarty (względem metryki zdefiniowanej w punkcie 7.14) wtedy i tylko wtedy, gdy 5 jest jednostajnie domknięty, jednakowo ciągły i punktowo ograniczony .(Jeżeli S nie byłby jednakowo ciągły, to posiadałby ciąg, którego żaden podciąg nie byłby jednakowo ciągły, a zatem żaden podciąg nie byłby jednostajnie zbieżny na K.)

20.    Jeżeli funkcja/ jest ciągła na <0,1> i jeśli

0

J/(x)xVx = 0 (n = 1, 2, 3,...),

to/(x) = 0 na <0,1>.

Wskazówka. Całka z iloczynu funkcji/ i dowolnego wielomianu jest równa zeru. Skorzystać z twierdzenia

i

0

Weierstrassa i pokazać, że\ f²(x)dx = 0.

21. Niech K będzie okręgiem jednostkowym na płaszczyźnie zespolonej, tj. zbiorem takich z, że |z| = 1, i niech st będzie algebrą wszystkich funkcji o postaci