Cialkoskrypt"5

irr

•i

448

6. Zadania różne

a₀ = 7kRT₀ = Vl,4 • 287 • 300 = 347,19 m/s,

RT₀ 287-300    2,87-3

Po ¹⁰ Po= —"-

¹⁰    = 1,16 kg/m³,

m* = A • p₀

2 V-> 2k

k +1

k - \

RX,

K + 1 _

= ^AP.:

2 V-i 2k

K+l

K + \J V K + 1

K+l

RT₀ =

I- I 2    |2(k-I)    [    2    ]2(k-I)

= A_Po._a/k-RT₀-|—₇|    - A • p_(> • a₀1 ^m

K + l

K + l

= 10^-4-1,16-347,19

= 0,023 kg/s.

1.4+1 2    32(1.4-0

1,4 + 1

Dla wyznaczenia strumienia masy płynącej przez szczelinę wyznaczmy związki pomocnicze:

stąd

JL

Po

f V

_P

^Po )

P =

L> _p _ Po ( k Po j RT₀ ^ _Po j

m = A -p-u = A

Po

^RTo iPoJ

u =0,01945 kg/s

oraz m / m* = 0,8467.

ZADANIE 6.15

■i-

W

-X

Przekrój wylotowy dyszy Lava!a w silniku rakietowym At = 0,5 m², liczba Macha zaś gazów wylotowych M, = 2,5 przy ciśnieniu 170 mm Hg, p_Hg = = 13 600 kg/m³. Obliczyć zmianę ciągu (funkcji pędu) po zmianie przekroju wylotowego A₂ = 0,6 m². Przyjąć k = i ,4.

Rozwiązanie

Z równania ciągłości dla najmniejszego przekroju A* (w tym przekroju M = 1) i dowolnego przekroju A (rys. 6.11)

A _ p*»u _:u_p*    _Pq    a*    a o    a    1

A* p ■ u    Po    p    a₍₎    a    u    M

2 (    K — 1 2

- 1 +-M²

K + ll 2

K+l

2(k-1)

Dla K = 1,4

6. Zadania różne

449

1    K-l.,,

1 + —M"

V 2

K

K-l

K + l

A (5 + M²)³ A* 216 M ’

Pl

Pi _ Pi Po    Po

P» Po P*    Pl

Po

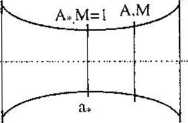
Rys. 6.11

A,.M,

Po podstawieniu M = M[ = 2,5 na podstawie powyższych zależności mamy:

Al = l^{5 + 2}’⁵ _L ₌ 2,6367188 oraz — = 1,1867.

A* 216-2,5    p*

Siła ciągu F = p • A + (pA - u)u . Ponieważ a² = Kp/p, więc p = Kp/a², M = u/a i mamy:

F_f = p • A • (l + kM² ) = 170 • 10'^? -13600 • 9,81 ■ 0,5(l +1,4 • 2,5²) = 110568 N.

Po zmianie przekroju

Al^Al.Al ₌ 2,6367-?4 = 3,164 = - ¹

A# A,

0,5

M„

K + l

. K-l-.i

1 +-M;

2 ²

2(K-t)

Stąd po rozwiązaniu powyższego równania względem M₂ otrzymujemy M₂ = 2,693 oraz

K

K-l

f    Y

Pg_

P*

t K 1 _ _ "7

1 +-M“

K

K-l

— = 1,2073 i J^- = —⁰⁷³ =1,0176, p*    pj 1,1867

K + l

więc F₂ = 112514 N oraz przyrost ciągu AF = F₂ - F| = 1946 N.

1