DSCN0525

2. (IwnKlna 8t« kincinulykii cwolwcnłowych przekładni walcowych

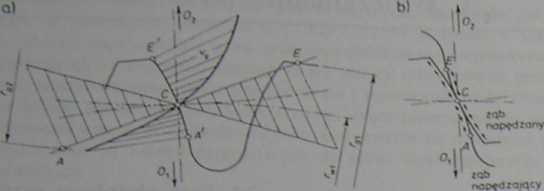
Rys 2.58. Zmiana prędkości poślizgu na czynnej części zarysu zęba: a) rozkład warrości poślizgu, b)

kierunki poślizgu

odbicie w niektórych opisach zjawiska pittingu i hipotezach jego powstawania. W badaniach laboratoryjnych i w praktyce potwierdza się ten pogląd, gdyż właśnie w strefie poślizgu ujemnego powstają na ogól pierwsze wykruszenia zmęczeniowe.

Jak wynika z naszej analizy, największe poślizgi występują w początkowych i końcowych punktach przyporu i zależą od odległości tych krańcowych punktów od bieguna zazębienia, która jest z kolei uwarunkowana wartością modułu m, i współczynnika przesunięcia zarysu x. Dla kół o takiej samej średnicy tocznej korzystniej będzie pod względem zmniejszenia poślizgu przyjmować mniejsze moduły i większą liczbę zębów. Za pomocą korekcji, przez odpowiednie dobranie współczynników- przesunięcia zarysu x, i x₂. można uzyskać wyrównanie poślizgów. czyli jednakowe ich wartości w krańcowych punktach przyporu A i £. Jest to korzystne ze względu na moc tarcia w zazębieniu i związane z tym nagrzewanie się przekładni.

Na rysunku 2.57 przedstawiono też zmianę prędkości i>„. toczenia się zębów po sobie, określonej wzorem:

Można tu jeszcze wspomnieć o sumie prędkości stycznych v_kl której wzrost sprzyja powstawaniu hydrodynamicznego ciśnienia oleju w zazębieniu, a tym samym tarciu płynnemu. Z kolei różnica prędkości stycznych, czyli poślizgu, jest przyczyną zużycia ściernego, zwłaszcza w warunkach skąpego smarowania lub przekładni otwartych. Intensywność ścierania zależy nie tyle od bezwzględnej wartości prędkości poślizgu, ile od poślizgu względnego, zdefiniowanego jako stosunek prędkości poślizgu do prędkości stycznej, a więc: dla zębów zębnika

dla zębów kola

(2.107)

».i

*> 2 =-

Zmianę poślizgu względnego na linii zazębienia przedstawiono na rys. 2.57.

2J5.2. Sprawność zazębienia

Straty mocy wskutek tarcia w mechanizmach ujmuje się za pomocą sprawności mechanicznej, którą w przypadku przekładni zębatej określimy jako stosunek mocy P₂ uzyskanej na wale wyjściowym (zdawczym) przekładni do mocy włożonej P, na wale wejściowym:

Całkowita strata mocy P, = P, — P₂ wynika z tarcia w różnych węzłach przekładni. a głównie:

—    w łożyskach i w uszczelnieniach obrotowych,

—    w zazębieniu wskutek tarcia współpracujących zębów,

—    w oleju wskutek jego mieszania przy smarowaniu zanurzeniowym.

Inne straty, np. wynikające z tarcia kół o otaczające powietrze i jego mieszanie, pomijamy jako znikome.

Sposób obliczania całkowitej sprawności przekładni przedstawiony jest w rozdz. 4, a tutaj zwrócimy uwagę tylko na sprawność samego zazębienia i stratę mocy wskutek tarcia zębów. Sprawność zazębienia jest stosunkiem mocy na zębach koła napędzanego do mocy na zębach koła napędzającego:

(1109)

Moc tarcia zębów może być zapisana ogólnym wzorem:

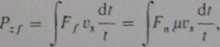
(2.110)

gdzie Ff jest siłą tarcia międzyzębnego, v_s — prędkością ślizgania się zarysów zębów (poślizgu), F_a - siłą normalną, n - współczynnikiem tarcia.

Parametry F_n, n i o_t w wyrażeniu (2.110) zmieniają swoje wartości podczas zazębienia. Siła normalna F_a pojawiająca się w punkcie styku zębów .4 zmienia swą wartość w sposób skokowy w punktach B i D przechodzenia z zazębienia jednej pary zębów w zazębienie dwóch par zębów. Oprócz tego, na skutek zmiennej sztywności zębów, siła ta zmienia nieznacznie swą wartość na całej długości odcinka przyporu. Rzeczywisty rozkład obciążenia międzyzębnego jest więc bardziej złożony, niżby to wynikało z rozkładu teoretycznego.

i