DSCN0515

66 2. Geometria i kinematyka cwolwenlowych przekładni walcowych

wzajemnie położone, aby okręgi zasadnicze się przecinały (rys. 2.38), gdyż tylko wówczas możliwe będzie poprowadzenie wspólnej stycznej do dwóch okręgów zasadniczych. Ta wspólna styczna jest przy zarysach ewolwentowych zębów linią przyporu zazębienia wewnętrznego.

Rys. 2.38. Przekładnia z zazębieniem wewnętrznym

Geometrię zazębienia wewnętrznego można opisać takimi samymi parametrami jak zazębienie zewnętrzne: u, a_w, a_w, e_a. Dzięki przyjęciu opisanej w pkt. 2.1.1 i 2.1.6 konwencji znaków plus i minus, obliczenia wartości tych parametrów przeprowadza się według tych samych wzorów co w zazębieniu zewnętrznym, przy czym należy pamiętać, że przełożenie i odległość osi w zazębieniu wewnętrznym będą miały wartość ujemną.

W porównaniu z przekładnią zewnętrzną geometria przekładni wewnętrznej jest bardziej złożona ze względu na możliwość wystąpienia różnych rodzajów zakłóceń zazębienia. Aby zazębienie wewnętrzne było poprawne, muszą być spełnione liczne warunki nieinterferencji. Istota niektórych warunków jest taka sama jak w zazębieniu zewnętrznym, ale w zazębieniu wewnętrznym zachodzi bezwzględna konieczność ich sprawdzania ze względu na znacznie szerszy zakres parametrów zazębienia, przy którym występuje interferencja. Poza tym istnieje jeszcze grupa warunków interferencyjnych właściwych tylko dla zazębienia wewnętrznego.

2.1.14. Interferencja w zazębieniu wewnętrznym

W zazębieniu wewnętrznym, w większym jeszcze stopniu niż w zazębieniu zewnętrznym, występują ograniczenia parametrów kół z warunków interferencyjnych. Początek zazębienia (punkt -4) musi leżeć powyżej punktu granicznego L, zarysu ewolwcntowego zęba zewnętrznego (rys. 2.39a), gdyż w przeciwnym razie (rys. 2.39b) wystąpi interferencja. Koniec zaś zazębienia (punkt F.) musi leżeć poniżej punktu granicznego L_t ewolwcntowego zarysu zęba wewnętrznego (rys.

2.39c), a nie odwrotnie (rys. 2.39d). Okręgi wierzchołków współpracujących kół w zazębieniu nie powinny więc wychodzić poza zakres określany punktami L_t i Lj na linii przyporu (rys. 2.40), obrazującymi położenie punktów granicznych zarysu ewolwentowego w zębach koła zewnętrznego i wewnętrznego. Interferencja może zachodzić zarówno u podstawy zębów wewnętrznych, jak i zewnętrznych.

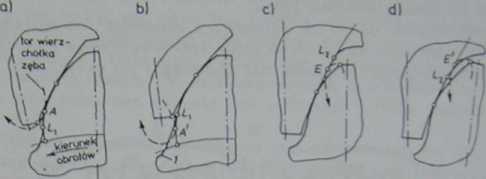
Rys. 2.39. Współpraca zębów w zazębieniu wewnętrznym: a) i c) bez interferencji, b) i d) z interferencją

Rys. 2.40. Schemat do sprawdzania warunków interferencyjnych

Interferencja wierzchołkowa zęba zewnętrznego z linią przejściową u podstawy zęba wewnętrznego nie wystąpi, jeżeli będzie spełniona nierówność:

(2.52)

(2.53)

12.54)

tfw-tfu >C.f

Wielkości g_w i Q_ti są ujemne i określa się je z zależności:

9w = (ł*2 + *M)tg#w,

6n ^{m r}n *S *i»»

gdzie P|2 i Ru wyznacza się z zależności (2.15) i (2.19).