DSCN0516

I

68_2. Geometria i kinematyka cwplwcntowych przekładni walcowych

Kolejny warunek nieinierferencji dotyczy obszaru wierzchołka zęba wewnętrznego i stopy zęba zewnętrznego i zapisuje się go następująco:

9w ~ Qii > Qo2-    (2.55)

Jeżeli omówione warunki nieinierferencji nie są spełnione, to należy albo zmienić parametry zazębienia (najczęściej współczynniki przesunięcia zarysów zębów), albo też zmienić wysokość zębów.

Przy niekorzystnie dobranych parametrach zazębienia wewnętrznego może wystąpić też interferencja wierzchołków zębów kola zewnętrznego z wierzchołkami zębów kola wewnętrznego. Przypadek taki zilustrowany jest na rys. 2.41a. Po lewej

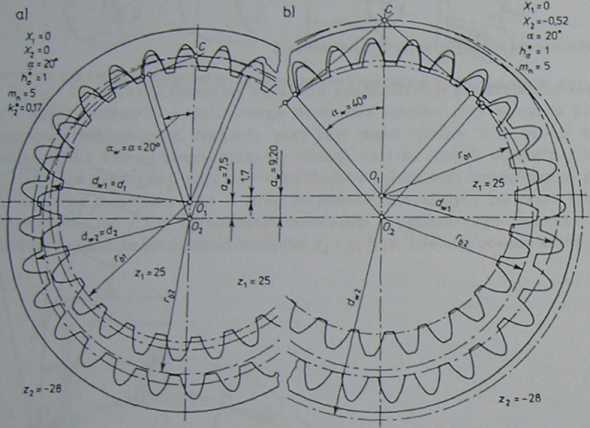
Rys. 2.41. Zazębienie wewnętrzne: a) z interferencją wierzchołków zębów, b) bez interferencji

stronie rysunku, w pobliżu poziomej osi, widać, że zarysy zębów przenikają się, uniemożliwiając oczywiście jakąkolwiek pracę przekładni. Interferencja ta występuje przy zbyt malej różnicy liczb zębów współpracujących kół oraz przy zbyt małej wartości tocznego kąta przyporu. Na rysunku 2.4Ib przedstawiono zazębianie się kół o tej samej liczbie zębów co na rys. 2.4la, jednak ze zmienioną wartością tocznego kąta przyporu, uzyskaną przez zmianę wartości współczynnika przesunięcia zarysu uzębienia wewnętrznego. Jak widać, przez zmianę wartości a_K. uzyskano zazębienie, w którym uniknięto interferencji.

2.1. Geometria kół walcowych o zębach prostych

69

b)

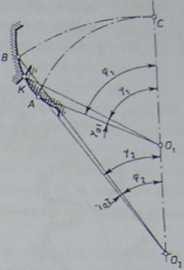
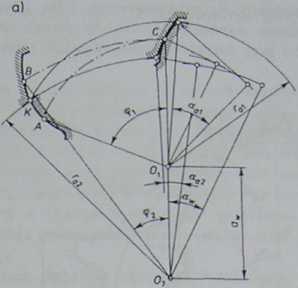
Rys. 2.42. Schemat do sprawdzania interferencji wierzchołków zębów

Graniczny przypadek, w którym występuje stykanie się wierzchołków zębów, przedstawiono schematycznie na rys. 2.42. Można z niego ustalić warunek niewystępowania interferencji wierzchołków zębów. Z zasady działania przekładni wynika równość długości łuków na okręgach tocznych kół: AC = BC, a stąd zależność:

(2.56)

(2.57)

|| _    _ -Zz

<Pi    2,

(u i z2 mają wartość ujemną).

Kąty <p, i <p₂ wyznacza się z zależności:

<Pi =yi+y«t.

<Pi = y₂-y_a2-

Korzystając z twierdzenia cosinusów, można z trójkąta O_zKO, wyznaczyć wartości kątów y, i y₂. Po podstawieniu y, i y₂ do równań (2.57) uzyskuje się zależność na obliczenie tp, i <p₂ -w postaci:

ai—rj₂ + r*,    .

<Pt =arccos—---ł-inva_Bl — inva_w.

<p₂ = arccos

|r_mla_w

al + rl₂-rl, 2r_a2a_w

+ inva_a2 — inva_w.

(2.58)

(2.59)

Warunek niewystępowania interferencji można zapisać w postaci:

(2.60)

Ł>-..

<P 2