DSCN0514

2. Geometria i kinematyka ęwolwcniowych przekładni walcowych

64

Po wstawieniu odpowiednich wyrażeń otrzymamy:

9. = *bi tg*.i + ^rbi tg    - fei + ^rbi) tg *»•    (²-⁴⁸)

lub też w innej postaci:

9* tf _nA,²i -rii + \/^rli — ^rłi — o» sinsc_w.    (2.49)

Ostatecznie wzór na wskaźnik przyporu (czołowego) dla zazębienia kół o zębach prostych przybierze postać:

łki tg«.i +'^-42tga_o2-('^,6i +^r62)tga_w _

₌ —-— =

nm_n cos a

= — [r, (tga„| -tgaJ + r₂(tga_o2-tgaJ]    (2.50)

2n

lub

| _ y/tii-rbi+s/r;₂-rł₂-a_ws\nz_w    g|j|

nm_R cos a

Wskaźnik zazębienia jest jednym z podstawowych parametrów charakteryzujących pracę zazębienia. Określa on, ile średnio par zębów bierze udział w zazębieniu. Jeżeli z. = 1, zazębiać się będzie zawsze tylko jedna para zębów. Jeżeli I < i_a < 2, w przyporze będzie raz jedna, a raz dwie pary zębów. Ilustruje to rys. 2.36, na którym łatwo zauważyć, że na odcinku od punktu A do punktu B oraz od punktu D do punktu E występuje dwuparowy przypór (współpracują dwie pary zębów). Na odcinku BD będzie występował jednoparowy przypór.

Punkt początkowy jednoparowego przyporu B leży w odległości p_b od końca odcinka przyporu (punkt £), a punkt D, będący końcem jednoparowego przyporu, leży także w odległości p_b, ale od początkowego punktu A odcinka przyporu.

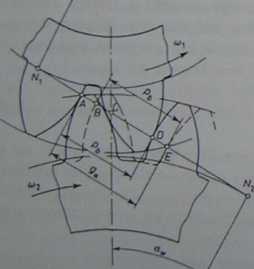
Rys. 2.36. Zazębienie przy I < e, < 2

Przechodząc od odcinka przyporu do powierzchni zęba (rys. 2.37), można stwierdzić, że strefa zazębienia tylko jednej pary zębów znajduje się w pobliżu środka wysokości zęba B'D'. W strefie zazębienia jednej pary zębów zęby przenoszą całkowite obciążenie, w strefie idealnego zaś zazębiania się dwóch par -teoretycznie tylko połowę obciążenia, gdyż obciążenie rozdziela się między dwie współpracujące pary zębów.

2.1.12. Interferencja zazębiania zewnętrznego

Prawidłowa teoretycznie współpraca zębów zachodzi wówczas, gdy zarysy ewolwentowe przylegają do siebie stycznie w każdym chwilowym punkcie przyporu. Naruszenie tego warunku mogłoby czasem wystąpić w obszarach brzegowych odcinka przyporu, tj. w obszarze współpracy wierzchołka jednego zęba z częścią stopową drugiego zęba, objawiając się wnikaniem wzajemnym obrysów obu współpracujących zębów, co nazywamy interferencją zarysów. W przypadku zazębienia obróbczego interferencja powoduje wycięcie przez zarys skrawający pewnych części z obszaru teoretycznego obrysu zęba nacinanego (podcięcie zęba u podstawy i ścięcie przy wierzchołku zęba). Skojarzenie zaś w przekładni rzeczywistej kół, które wykazywałyby interferencję, spowoduje dodatkowe siły i odkształcenia elementów przekładni oraz wycieranie i wygniatanie materiału w obszarze interferencji. Są to zjawiska bardzo niekorzystne i niepożądane i dlatego konstruktor powinien sprawdzić, czy nie występuje interferencja i tak projektować przekładnię, aby jej uniknąć. Konieczność takiego sprawdzania istnieje w przypadku, gdy zęby mają być nacinane dłutakiem.

Sposób postępowania przy sprawdzeniu niewystępowania interferencji można znaleźć np. w pracy [45].

2.1.13. Parametry przekładni wewnętrznej

Przekładnia wewnętrzna składa się z dwóch 'kół, z których jedno — mniejsze — ma zęby zewnętrzne, drugie zaś ma uzębienie wewnętrzne. Aby możliwe było spełnienie warunku stałości przełożenia, środki tych dwóch kół muszą być tak

i - Przekładnie zębate