DSCN0520

2. Geometria i kinematyka cwoiwenipmych pfzeklaJm walw*>e>>

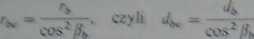
12.71)

Uwzględniając proporcję:

<4. 4

<4.    <Ł^%

(2.72)

możemy napisać:

Wielkość <4 określa średnicę koła podziałowego zastępczego. Odpowiadającą jej zastępczą liczbę zębów (o module ntj otrzymamy po przekształceniu zależności:

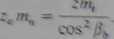
(2.74)

A więc

(2.75)

(2.76)

cosr&cos/T

Można też stosować wzór:

cos^J/T

który wynika z zależności geometrycznych dla elipsy uzyskiwanej z przekroju walca podziałowego.

Z zastępczej liczby zębów korzysta się też przy ustalaniu (z pewnym przybliżę-mcm) granicznych wartości parametrów uzębienia ze względu na podcięcie lub zaostrzenie u wierzchołka. Ponieważ przy ($ ?t 0 zastępcza liczba zębów z_u jest większa od rzeczywistej, możliwe jest zastosowanie w kołach z zębami skośnymi mniejszej liczby zębów niż w kołach z zębami prostymi, bez obawy podcięcia lub zaostrzenia ich u wierzchołka.

2.2J. Odległość osi kół

Dwa koła zębate walcowe z zębami śrubowymi utworzą prawidłową przekładnię o osiach równoległych wówczas, gdy zęby obu kół wykonane będą według tego samego zarysu odniesienia oraz gdy będą miały przeciwne kierunki pochylenia linii śruoowych, a więc prawy i lewy, oraz taki sam kąt pochylenia Unii śruoowej zęba IJ_b Irys. 2.51) lub, co jest jednoznaczne, kąt IS.

Ik

2.2 Ocomcuui kół walęowych o izbach skośnych

Ze względu na występowanie prawidłowej ewolweniy w przekroju czołowym, a stąd możliwości uzyskania wprosi zależności związanych z kształtem ewolweniy. obliczenia zazębienia śrubowego przeprowadza się najczęściej dla lego przekroju.

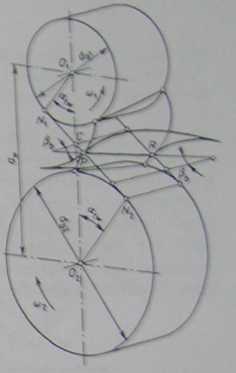
Rys. 2.51. Współpraca powierzchni cwolwcntowych w zazębieniu skośnym. PR — linia styku zębów

Wówczas wzory dotyczące zazębienia kół walcowych o zębach prostych nadawać się będą do obliczeń zazębienia śrubowego, oczy wiście, jeżeli podstawi się do nich odpowiednie wielkości geometryczne określone dla przekroju czołowego.

Korzystając z wzorów (2.37) i (2.66), możemy obliczyć odległość osi kół skośnych:

Ur+CjJm, cos a,    (c_l + c>)m„ cos a,

u ₌ .........-    =    ■ -    (2.77)

2 COS3t,_w    2 COs/f COS Oj.

Potrzebny tu kąt przyporu toczny w przekroju czołowym obliczamy z funkcji ewolwentowej [wzór (2.41)]:

x.+ x> _s    __

mvct,„ = 2tgo_n-+ 11^0*..    (2.7S)

Ji+*ł

Toczny kąt przyporu x_ow dla przekroju normalnego obliczamy z zależności;

tg*₀w = tg^cos^.    (2.79)

Należy przy tym pamiętać, że wszystkie współczynniki wysokościowe zęba (/ij. c*. x_t i x₂), a więc i występujące we wzorze (2.7$) współczynniki przesunięcia zarysu zębów, odnoszone są do modułu normalnego ze względu na to, że parametry w przekroju normalnym związane są ze znormalizowanym zarysem odniesienia.