DSCN0509

I

54_2. Geometria i kinematyka cwolwcntowych przekładni walcowych

Ze względu na to, że linia toczna obtacza się bez poślizgu po okręgu podziałowym, długość odcinka AB musi być równa długości luku GH, określającego grubość zęba na okręgu podziałowym. Stąd

s = ^ + 2xm.tg«.    (2.27)

Grubość zęba na dowolnym okręgu o promieniu r_y można wyznaczyć z zależności (rys. 2.24):

^st ~ ^ry $9 ~ ^r9 W+2 inv a - 2 inv a_y).    (2.28)

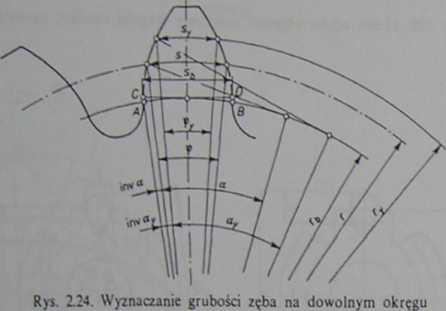
Kąt ifr jest kątową grubością zęba na okręgu podziałowym i wynosi

(2.29)

r

kąt a, zaś jest kątem zarysu ewolwenty na promieniu r_y. Podstawiając r = zmj2, otrzymujemy ostatecznie

s_f = 2r,^+~—+invsc-inva,^.    (2.30)

W szczególnym przypadku na okręgu zasadniczym grubość zęba s_b (odległość między ewolwenlami tworzącymi zarys boczny zęba AB, rys. 2.24) wynosi

_{lł = 2},_tg₊^_+inv^.    (2.31)

Jest ona równa grubości zęba CD, mierzonej wzdłuż stycznej do okręgu zasadniczego.

Jak już wspomniano, wraz ze wzrostem współczynnika korekcji zmniejsza się

2.1. Geometria kół walcowych o zębach .prostych

55

grubość zęba u wierzchołka. Przy pewnych wartościach x może wystąpić nawet zaostrzenie zęba u wierzchołka (rys. 2.25). Jest to zjawisko niepożądane, gdyż ząb taki łatwo może ulec przeharlowaniu u wierzchołka, co stwarza niebezpieczeństwo

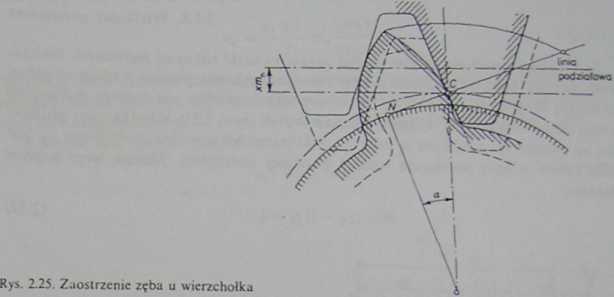
wykruszenia pod obciążeniem eksploatacyjnym. Należy więc dążyć do tego, aby grubość zęba u wierzchołka nie była mniejsza od dopuszczalnej. Wymagana grubość u wierzchołka, a w granicznym przypadku jego zaostrzenie, ogranicza obszar dopuszczalnego dodatniego przesunięcia zarysu (rys. 2.26). Przyjmuje się najczęściej minimalną grubość zęba u wierzchołka dla uzębień o jednolitej strukturze materiału s_u(mn = 0,25 m_n, a dla uzębień o niejednorodnej strukturze (nawęgla-nie, hartowanie powierzchniowe) s_limin = 0,4 m„. Przy modułach dużych, większych od 10 mm, minimalna względna grubość u wierzchołka może być mniejsza.

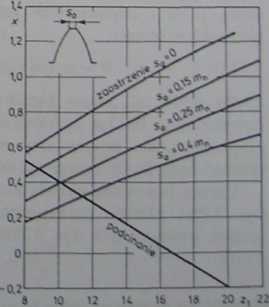
Rys. 2.26. Przybliżone, graniczne ze względu na zaostrzenie i podcięcie, współczynniki przesunięcia zarysu w funkcji liczby zębów z, (a = 20°. h* = I)