DSCN0524

85

84

2. Geometria i kinematyka cwolwcntowych przekładni walcowych

2.3. Kinematyka przekładni walcowych

W biegunie zazębienia t>_k, = v_ki (rys. 2.57). a zatem poślizg maleje do zera. czyli w tym punkcie wystąpi czyste toczenie. Z lego powodu biegun zazębienia C nazywany jest czasem punkiem tocznym.

Jak mogliśmy zauważyć, prędkości poślizgu dla zębnika i kola mają tę samą wartość bezwzględną, różnią się zaś tylko znakiem. Z kierunkiem poślizgu związany jest kierunek sil tarcia międzyzębnego, co jest zaznaczone strzałkami na rys. 2.58. Na zębach napędzających mają one kierunek od bieguna zazębienia C na zewnątrz — odbiegu nowy, a na zębach napędzanych ich zwrot jest przeciwny -dobiegunowy. Sens rozróżniania poślizgu ujemnego i dodatniego tkwi w tym, że ujemny sprzyja powstawaniu pittingu, a dodatni przeciwnie. Znajduje to swoje

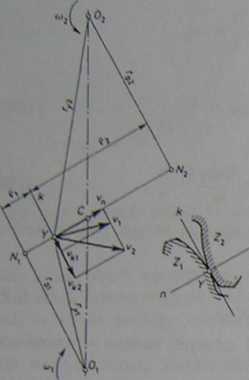
Rys. 2.56. Rozkład prędkości w chwilowym punkcie przyporo

oraz

Wpm ĘM    (2.99)

Prędkości te maju składowe: v_n - skierowaną wzdłuż wspólnej normalnej n zarysów Z, i Z₂ oraz o_k - wzdłuż wspólnej stycznej k. Składowe normalne prędkości obu zarysów muszą mieć ten sam kierunek i wartość, gdyż w przeciwnym razie nastąpiłoby oddalenie się od siebie zarysów (przerwanie przyporu) lub wnikanie jednego zarysu w drugi (interferencja):

= Ifj <*>'i = Ki = r_b2 (Oj = v_n.    (2.100)

Składowe prędkości w kierunku stycznym można wyznaczyć z rys. 2.56, wykorzystując podobieństwo trójkątów, lub wprost jako iloczyn prędkości kątowej i promienia prostopadłego do kierunku wektora wyznaczanej prędkości:

(2.101) (2.102)

(2.103)

(2.104)

Si = Qi<»i

oraz

v_k2 =Qi<D ₂.

Różnica tych prędkości wyznacza wartość poślizgu międzyzębnego: dla zębnika

u„ = 0_ftł-V_k2.

dla kola

Punkty charakterystyczne

i	c	Nl
Cl - o	Ci " rM tga„	Ci = <iwsinocw
$1 - o	0»i ““iCi	0»i -<o,p,
Oi ^m <ł„$ina„	C: = rM Iga.	Cj “0
fki — u>i01	0»i “ ^wiCi	0»i -0
li ■ -fu	t),i = 0	».i = ||j
0.1 - 0»i	o,i = 0	0.1 “ -0»l
!»<= p	0- = »U = 0»1	t II o
Cl “ - co	i -o	Cl = 1
Ci" i	Ci - o	Cl = -»

Rys, 2.57. Zmiana charakterystycznych prędkości na linii zazębienia. 1 i t>„ - prędkości styczne, i>„ i i>,j - prędkości poślizgu, -prędkość toczenia. Ci * Cr — poślizg względny

®«1 =