DSCN0504

44 2 Geometria i kinematyka cwolwcnlowych przekładni walcowych

44 2 Geometria i kinematyka cwolwcnlowych przekładni walcowych

ręt>a

"orfftfno -Zfbotki

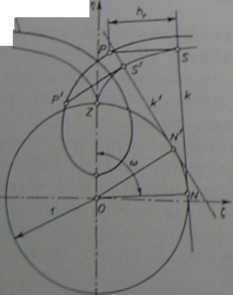
Rys. 2.11. Powstawanie linii przejściowej przy nacinaniu narzędzicm-zębalki)

bez poślizgu po okręgu o promieniu r. Równanie cwolwcnty wydłużonej w układzie współrzędnych prostokątnych £, tj (rys. 2.12) można przedstawić w postaci:

(2.10)

£ = r sin w — roj cos co — li, sin w, ij = r cos oj + rw sin oz — h, cos w.

gdzie kąt <u jest kątem wychylenia promienia wodzącego punktu styku N linii tocznej k i okręgu o promieniu r.

Dowolny punkt F leżący na torze środka zaokrąglenia u wierzchołka zęba narzędzia oraz całkowity zarys linii przejściowej można wyznaczyć graficznie według schematu przedstawionego na rys. 2.11. Odpowiadające punktowi F

reełwento

wydłużono

Rys. 2.11 Ewolwenta wydłużona

położenie linii tocznej narzędzia zaznaczone jest na rysunku. Linia ta jest styczna do okręgu (ocznego (podziałowego) w punkcie F. Punkt F leżący na linii tocznej w ruchu względnym narzędzia przemieścił się do punktu F. Długość luku C₀F' równa jest więc długości odcinka C₀F. Podobnie, długość odcinka H'F' jest równa długości odcinka HF. Odcinek HP, który łączy środek zaokrąglenia u wierzchołka zęba z linią toczną, przyjmuje, wraz. z przemieszczeniem się linii, nowe położenie H'F, wyznaczając w ten sposób miejsce punktu F. Linia przejściowa powstająca jako obwiednia kolejnych położeń zarysu zęba narzędzia kształtowana jest w procesie nacinania przez luk zaokrąglenia zęba u wierzchołka. Kreśląc więc luki o promieniu q_o0, otrzymuje się graficznie jej zarys. Będzie ona ekwidystantą toru środka zaokrąglenia P, czyli ekwidystantą ewolwenty wydłużonej.

W przypadku nacinania dłutakiem modułowym konstrukcja zarysu linii przejściowej jest podobna (rys. 2.13), a powstająca linia przejściowa zębów zewnętrznych ma kształt ekwidystanty wydłużonej epicykloidy lub częściej, jeżeli p,₀ = 0, po prostu wydłużonej epicykloidy, w zębach zaś wewnętrznych - wydłużonej hipocykloidy.

zarys linii przejściowej (ekwidystantą epicykloidy wydtuionej)

Rys. 2.13. Powstawanie linii przejściowej przy nacinaniu dłutakiem

Wydłużona epicykloida powstaje jako linia zakreślona przez punkt P (rys. 2.14), przemieszczający się wraz z okręgiem o promieniu r_w0, przetaczanym po drugim okręgu o promieniu r_wl. Równanie epicykloidy wydłużonej w układzie współrzędnych (, tj można przedstawić w postaci:

(2.11)

C = a_wo^sm<w—rrO^S,n ww.

rj = u_w0 cos oj - r_r0 cos woj.

gdzie kąt aj jest kątem wychylenia promienia wodzącego łączącego środki 0₀ i C>|, a odległość osi w zazębieniu obróbczym <i_w0 i wielkość »v wyznacza się