DSCN0522

i

i

80

2 Geometria i kinematyka cwolwcntowych przekładni walcowych

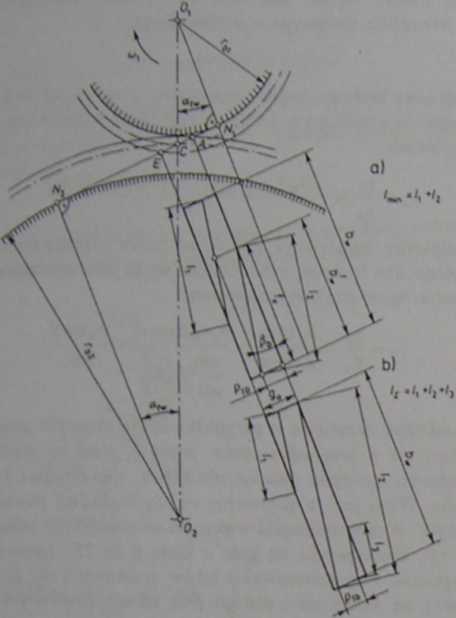
Rys. 153. Długości linii styku zębów w zazębieniu skośnym

odcinek Ponieważ jednak dochodzi jeszcze odcinek l₃ zwiększający swą długość _t wraz z obrotem kół, całkowita długość linii styku będzie się zwiększać. Przesuwa-< jąc w wyobraźni w dalszym ciągu linie styku zauważymy, że po pewnym czasie całkowita długość linii styku zębów będzie się zmniejszać, aż znowu osiągnie swą : minimalną wartość.

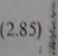
Łatwo też można sobie wyobrazić, że w sytuacji gdy szerokość zazębienia , wynosi

LI    P*

"    Ig A

lub wielokrotność tej wartości, a więc gdy =» 1,2, 3,... (liczba całkowita), sumaryczna długość linii styku nie będzie się zmieniać. Podobna sytuacja zaistniej je, gdy t, - 1.

W idealnym zazębieniu kół o zębach śrubowych obciążenie rozkłada się na poszczególne zęby proporcjonalnie do długości linii styku i,, i l₃. Nacisk

jednostkowy na zęby zmniejsza się oczywiście wraz ze wzrostem sumarycznej długości linii styku l_t. W obliczeniach wytrzymałościowych istotna jest znajomość minimalnej wartości /_Ł.Przy n_t + n_f> 1 można ją wyznaczyć z wzoru:

(2.S6)

.    ( .    (1 — «,).(! -/T),) 1    h_wc,

^miR~ cos fi, [    c,Cg J COS& *’

a przy n, + n_# < I z wzoru:

I

min

cos fi, \ Cl c₀ /

(187)

gdzie n, i iig s«\ częściami ułamkowymi wartości wskaźników zazębienia c₂ i c_t (np. dla e, = 1,47 będzie n_a = 0.47).

Korzystny dla pracy przekładni jest przypadek, gdy U = const. wtedy bowiem jednostkowe obciążenie na długości linii styku zębów jest też stale (przy stałej sile obwodowej na kole), a tym samym zmniejszają się głośność przekładni i obciążenia dynamiczne.

2.16. Wielkości pomiarowe

Podobnie jak w kołach o zębach prostych, sprawdzenia grubości zębów śrubowych można dokonać m.in. metodą pomiaru wzdłuż wspólnej normalnej W (rys. 2.54). W płaszczyźnie czołowej długość odcinka IV) oblicza się tak jak dla zębów prostych (pkt 2.1.8):

W, = »i,cos<x, [(z_w-0,5)Jt + 2x,tga, + r inva,].    (188)

przy czym liczbę zębów objętych pomiarem z_w określa się za pomocą wykresu z rys. 2.28, przyjmując do jej określenia zastępczą liczbę zębów [wzór (2.75)]. Na podstawie rys. 2.54 można napisać zależność między W a IV) w postaci:

W= W_t cos    (2.89)

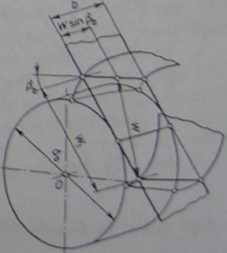
Rys. 2.54. Wyznaczanie długości pomiarowej IV'wzdłuż wspólnej normalnej zębów skośnych

* - WickUJKW lębaK