DSCN0501

.w 2. Geometria i kinematyka ewolwcntowych przekładni walcowych

Zarys zęba jesi symetryczny. W odległości s (rys. 2.1) mierzonej po luku okręgu podziałowego przebiega ewolwenta w przeciwnym kierunku. Tak więc cały obrys zęba wyznaczony jest fragmentem ewolwenty między punktami L i K oraz symetrycznie L' i K' po drugiej stronie zęba (rys. 2.2), lukiem okręgu wierzchołków

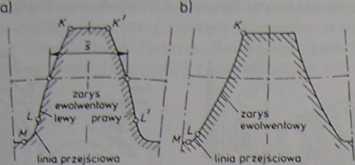
Rys 2.1 Zarys zęba: a) zewnętrznego, b) wewnętrznego

KK\ okręgu stóp oraz tzw. linią przejściową LM. Zarys zęba będzie określony, jeżeli podane zostaną: r — liczba zębów;

x_a - kąt przyporu na średnicy podziałowej równy nominalnemu kątowi zarysu;

- moduł, a tym samym średnica podziałowa d = rm_n;

(/„ — średnica wierzchołków; d_f - średnica podstaw;

s - grubość zęba mierzona na luku okręgu podziałowego, oraz jeżeli znany będzie kształt linii przejściowej, zależny od przesunięcia zarysu i technologii wykonania uzębienia.

Proporcje wymiarowe zębów ewolwentowych odniesione do modułu zostały znormalizowane i podawane są jako tzw. zarys odniesienia. Ułatwiło to w głównej mierze obróbkę uzębień, zmniejszyło bowiem liczbę typów i wielkości narzędzi.

2.1.2. Zarys odniesienia

Zarys odniesienia to zarys zębów zębatki, którą nazywa się zębatką odniesienia. Znormalizowane zarysy odniesienia podane są w normie PN-78/M-88503 i dotyczą kół zarówno walcowych jak i stożkowych o modułach m_n % I mm. Zarys odniesienia uzębień kół walcowych przedstawiono na rys. 2.3. Zaznaczona jest na nim linia podziałowa zębatki, tj. linia przebiegająca na takiej wysokości, że mierzone na niej grubości zęba i szerokości wrębu równe są połowie podziałki s = ^e = lp = Znormalizowane wymiary odniesione są do modułu normalnego m„ i wynoszą:

i wysokość prostoliniowego zarysu zębów h, = 2/i* m„ = 2m_n, przy czym linia

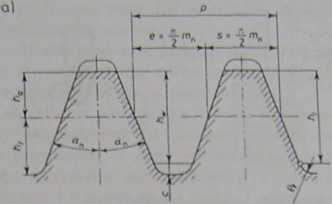
bł

Rys. 2.3. Zarys odniesienia: a) zębatka odniesienia, b) modyfikacja zarysu u wierzchołka zęba. m, -moduł normalny według PN-78/M-88502, a„ - kqi zarysu normalnego (a. = 20*). h. - wysokość głowy zęba (/i_d = I m_n), h_f - wysokość stopy zęba (h_f = 1,23 m„), h, - wysokość graniczna zęba, h_ -wysokość przenikania (łi„ = 2m_n), c — luz wierzchołkowy (c = 0,2$ m,,|, g_t - promień krzywizny

krzywej przejściowej

podziałowa przechodzi w połowie tej wysokości (/i* - współczynnik wysokości głowy zęba zarysu odniesienia, /i* = I);

—    luz wierzchołkowy (pkt 2.10): c = c*m_n = 0,25 m_n;

—    promień łuku przejściowego (linii przejściowej) g_f = Q*m_n = 0.38 m„.

Dopuszcza się, aby w technicznie uzasadnionych przypadkach przyjmować

wartość współczynnika luzu wierzchołkowego c* z zakresu 0,25 -fO,35 przy obróbce kół zębatych dłutakami i wiórkownikami oraz do wartości c* = 0,4 przy szlifowaniu. Dopuszcza się także, aby przyjmować q} ^ 0,38.

W celu poprawienia współpracy kół pod obciążeniem zaleca się, aby stosować modyfikację zarysu zębów polegającą na ścięciu części zarysu odniesienia u wierzchołka zęba. Polskie Normy dopuszczają prostoliniowe ścięcie na wysokości do h_a — 0,45 m„ o 'maksymalnej głębokości do Aa = 0,01 ni, (rys. 2.3b).

2.1.3. Technologiczne zasady kształtowania uzębień

Zęby kół walcowych wykonywane są zasadniczo dwiema metodami: kształtową i obwiedniową. Obróbka kół zębatych metodą kształtową może być przeprowadzona frezowaniem, dłutowaniem, przeciąganiem lub szlifowaniem. Na rysunku 2.4 pokazano dwa sposoby frezowania zębów metodą kształtową: frezem krążkowym i frezem palcowym. Zarys narzędzia odpowiada zarysowi wrębu. Narzędzie wykonując oprócz ruchu obrotowego / (skrawającego) ruch posuwisty 2 wzdłuż linii zęba kształtuje zarysy wrębów (zębów) na całej szerokości wieńca zębatego.

Obróbka kół zębatych walcowych metodą kształtową jest mało wydajna i mało dokładna. Istnieje również konieczność wykonywania narzędzia oddzielnie dla każdego rodzaju uzębienia różniącego się np. modułem, liczbą zębów, przesunięciem zarysu (korekcją) itp. Stosuje się ją obecnie jeszcze do wykonywania kół o