DSCN0519

74 2. Geometria i kinematyka cwolwcntówych przekładni walcowych

Stąd

=    (2.65)

Średnica walca podziałowego wynosi

<^2M>

a walca zasadniczego

M,= Ę cos a,.    (2.67)

Kąt pochylenia linii śrubowej zębów skośnych jesl inny na walcu podziałowym, a inny na walcu zasadniczym czy wierzchołkowym lub tocznym. Wynika to stąd, że skok linii śrubowej zęba p. na każdym walcu musi być taki sam, a obwód

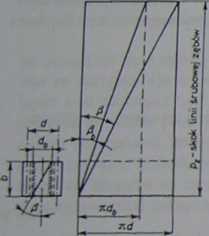
Rys. 2.49. Schemat do wyznaczania zależności między kątami 1 i Pb

zależy od średnicy walca. Dlatego zgodnie z rys. 2.49 kąty pochylenia linii zęba na i różnych walcach będą różne, a wartości ich zależeć będą od średnicy kół. Można $ to zapisać zależnością:

(2.68) \ I

I

nd_k ml nd_w nd_a

tg Pt ~ tg P ~ tg P_w ~ tg P_a ~ ^P:

Po przekształceniu uzyskuje się:

tgft tg P

d_±

d

= cos a,.

(2.69) I

2.2.2. Zastępcza liczba zębów

Kształt zębów skośnych, uwzględniany m.in. w obliczeniach wytrzymałościowych, rozpatruje się w płaszczyźnie przekroju normalnego zębów. Ząb w tym przekroju nie ma prawidłowego zarysu ewolwentowego. Analityczny opis jego

2.2. Geometria kół walcowych o zębach skoinych

75

kształtu musiałby być więc inny niż dla zębów prostych. W celu jednak ujednoliceniu i uproszczenia obliczeń wytrzymałościowych zwilżanych z kształtem zęba poszukuje się takiego kola zastępczego o zębach prostych, którego zęby będą miały kształt zbliżony do kształtu zębów skośnych w przekroju normalnym. Umożliwia się przez to wykorzystanie do obliczeń wytrzymałościowych zębów skośnych tych samych zależności co dla zębów prostych.

Rozpatrując uzębienie w płaszczyźnie przekroju normalnego zęba (rys. 2.50) przyjmujemy, że zęby rozmieszczone są na obwodzie elipsy, wynikającej z tego skośnego przekroju walca. Okrąg ściśle styczny do elipsy będziemy uważać za

okrąg koła zastępczego, na którym możemy sobie wyobrazić zastępczą liczbę zębów o podziałce normalnej p_n = nm_n. Okrąg ten ma promień równy promieniowi krzywizny elipsy w punkcie F. W literaturze spotkać można dwa różne podejścia przy wyznaczaniu zastępczej liczby zębów. W pierwszym elipsa wyznaczona jest na walcu zasadniczym koła, w drugim — na walcu podziałowym.

Pierwszy sposób wykorzystywany jest częściej, szczególnie przy rozpatrywaniu zagadnień związanych z technologią wykonania uzębienia, drugi zaś - ze względu na prostszą postać otrzymywanych wzorów - stosowany jest chętnie w obliczeniach wytrzymałościowych.

Rozpatrzmy elipsę uzyskaną w przekroju walca zasadniczego, płaszczyzną prostopadłą do linii śrubowej na tym walcu, a więc z uwzględnieniem kąta /ł».

Korzystając ze znanych zależności dla elipsy oraz oznaczając wielkości związane z kołem zastępczym indeksem v, możemy napisać:

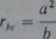
Po podstawieniu do tej zależności a = —oraz b = r_b otrzymujemy:

cos f}>