Image89

176

Jeżeli w dodatku £(#,) jest kwadratową funkcją q_lt tzn.

176

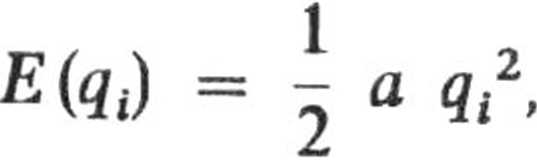
wówczas

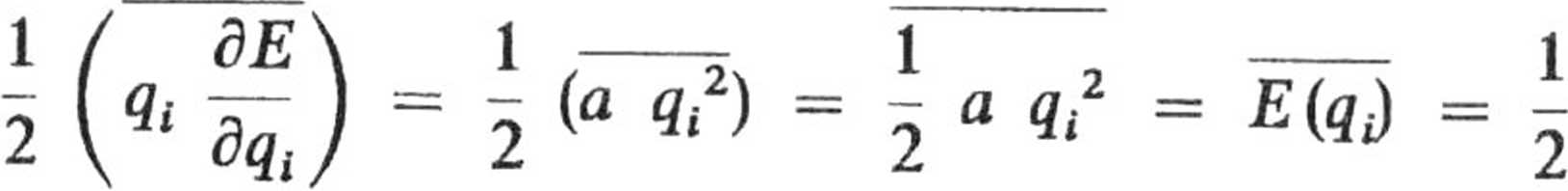
b. Z zasady ekwipartycji energii mamy:

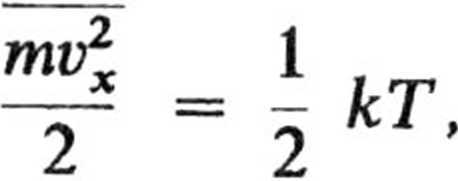
tak, że

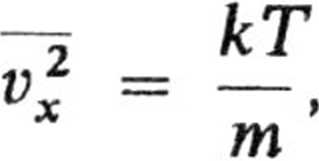
Zate

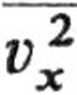
+ v

3kT

m

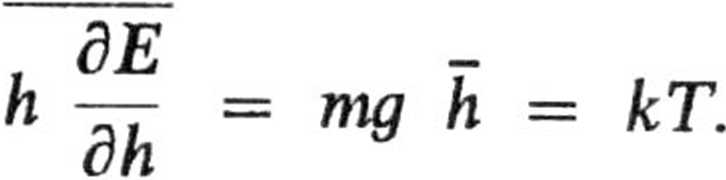
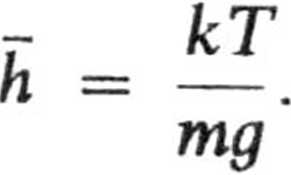
7. ZJAWISKA TRANSPORTU

7.1

a. Równanie opisujące przepływ ciepła znajdziemy opierając się na prawie Fouriera. Przy ustalonym prądzie cieplnym przez powierzchnię kulistą o promieniu x w czasie t przepłynie ilość ciepła Q, gdzie

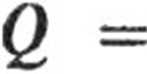
— 47t Xx ²t

dT

di'

Po rozdzieleniu zmiennych otrzymuje

II

y równanie

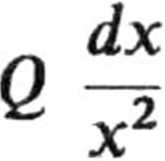
— 4ti Xt dT,

z którego po scałkowaniu w granicach od R_x do R₂ oraz odpowiednio od T_{ do T₂ mamy

Q = 4nXt (T_x

T₂)

R₂R

R₂ R_{

b. Rozkład temperatury w przestrzeni między powierzchniami kulistymi otrzymamy całkując równanie w granicach od R_l do x oraz od 7) do T. Wtedy

R_x x

Qi = 4nXt (T_x - T)

W stanie ustalonym ciepło przepływające przez dowolną powierzchnię kulistą jest jednakowe. Z równości

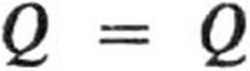
i

otrzymuje

II

y szukany rozkład

T =

Ki R₂ (J\ -

(R₂ - R_t)

R₂ Jz

r₂ -

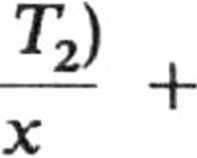
^Rl ^Tl

Rt