img057

122 II |_r Nieparametryczne testy istotności

3.10,    Na podstawie danych liczbowych z zadania 1,16 zweryfikować na poziomie istotności a =0,05 hipotezę, te rozkład wytrzymałości na ściskanie badanego betonu jest normalny.

3.11.    Na podstawie danych liczbowych z zadania 1.44 zweryfikować na poziomie istotności y =0,10 hipotezę, żc rozkład jednostkowego kosztu produkcji tego artykułu jest rozkładem normalnym o odchyleniu standardowym 24 zł.

§ 3.2 TEST ZGODNOŚCI X KOLMOGOROWA

Podstawowe wyjaśnieni*

Drugim podstawowym testem zgodności, obok testu y¹, j*st nieco mniej pracochłonny test zgodności Kołmogorowa, oparty na statystyce X,

Podczas gdy w tekście y¹ dla zweryfikowania hipotezy, że populacja ma. określony typ rozkładu, rozpatruje się liczebności szeregu empirycznego i porównuje się je z liczebnośćiami szeregu hipotetycznego, to w teście X KoJtnogorowa porównuje się dystrybuantę empiryczną i hipotetyczną. Jeśli bowiem populacja generalna ma rozkład zgodny z hipotezą, to wartości dystrybuanty empirycznej i hipotetycznej powinny być we wszystkich badanych punktach zbliżone. Punktem wyjścia w teście A jest analizowanie bezwzględnych wartości różnic między tymi dwoma dystrybuanłami. Największa różnica służy do budowy' statystyki X, której rozkład, niezależny od postaci dystrybuanty hipotetycznej, podał Kołmogorow, Rozkład ten służy do budowy obszaru krytycznego w omawianym teście, przy' czym jeżeli maksymalna różnica w pewnym punkcie obszaru zmienności badanej cechy jest zbyt duża, to hipotezę, że rozkład populacji ma taką dystrybu-antę jak przypuszczamy, należy¹ odrzucić. W tablicach statystycznych można znaleźć dokładny rozkład statystyki X Kołmogorowa, aie znacznie częściej korzysta się w praktyce z granicznego rozkładu, tzn. z dużej próby. Grupując wtedy dużą próbę w klasy należy to czynić tak, by nie były one zbyt szerokie (tzn. powinno ich być dużo).

Bardzo ważnym założeniem stosowalności testu X Kołmogorowa jest, aby dystrybuauta hipotetyczna była ciągła. Do badania zgodności z rozkładem skokowym nie można więc używać testu A, a tylko testu y². Ponadto,

przy stosowaniu testu zgodności X Kołmogorowa, w zasadzie parametry hipotetycznego rozkładu powinny być znane, jednakże gdy próba jest duża, to można je szacować z próby .

Z testem zgodności /. Kołmogorowa wiąże się test Kołmogorowch .Smirnowa dla weryfikowania hipotezy, ź'e dwie próby pochodzą z tej samej populacji, tzn. że dwie populacje mają ten sam rozkład. Rozpatruje się w tym teście różnice między' obu dystrybuantami empirycznymi. Graniczny rozkład odpowiedniej statystyki, z jakiej korzysta się przy budowie obszaru krytycznego dla tego testu; jest taki sarn jak graniczny rozkład statystyki X jtobnogorowa. Testu tego można też używać tylko dla ciągłych rozkładów badanej cechy. W podanych niżej modelach omówione są szczegóły obu testów.

Modd L Populacja generalna ma rozkład ciągły o dystrybuancie F(x). Z populacji tej wylosowano niezależnie do próby h elementów (n co najmniej kilkadziesiąt). Na podstawie wyników tej próby należy zweryfikować hipotezę H₀ \ F(x) = Fq(x), gdzie Fo(x) jest konkretną, hipotetyczną i ciągłą dystrybuantą.

Test istotności dla tej hipotezy jest następujący. Wyniki próby porządkujemy w kolejności rosnącej lub grupujemy je w' stosunkowo wąskie przedziały, o prawych końcach Xj i odpowiadających im liczebnościach n_s. Wyznaczamy dla każdego x_s wartość tzw, empirycznej dystrybucmty F_n{x) według wzoru

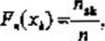
(3.2)

gdzie oznacza skumulowaną od początku aż do X* liczebność, tj.

ⁿ*= Z";-

Z rozkładu hipotetycznego wyznaczamy następnie dla każdego x_} wartość teoretycznej dystrybuanty F(x). Obliczamy dalej dla każdego x_s bezwzględną wartość różnicy F„(x) - F(x), tj. dystrybuanty empirycznej i teoretycznej. Z kolei obliczamy wartość statystyki (3.3)

X