img042 2

92 II. Parametryczne testy istotności

2.80. Na podstawie danych liczbowych 2 zadania 2.40 sprawdzić hipotezę o jednakowym rozrzucie wyników pomiarów frakcji pewnego białka w moczu królików w grupie kontrolnej i w grupie z badanym preparatem farmaceutycznym. Przyjąć poziom istotności 2=0,05.

2*81. W celu porównania regularności uzyskiwanych wyników sportowych dw u oszczepników, wylosowano 20 wyników rzutu oszczepem zawodnika A i 16 wyników zawodnika B. Otrzymano dla zawodnika A odchylenie standardowe wyników rzutu oszczepem wynoszące s- 2,65 m, a dla zawodnika B wynoszące 5=4,80 m. Na poziomie istotności a =0,10 sprawdzić hipotezę o większej regularności wyników zawodnika A.

§ 2.7. TEST JEDNORODNOŚCI WIELU WARIANCJI

Podstawowe wyjaśnienia

Niekiedy badamy ze względu na pewną cechę mierzalną więcej niż dwie populacje generalne. Test omówiony w tym paragralic jest pewnym uogólnieniem na przypadek porównywania wielu wariancji testu podanego w poprzednim § 2.6. Dotyczy on przypadku populacji normalnych, dla których chcemy sprawdzić hipotezę o równości wariancji we wszystkich populacjach. Ten test na jednorodność wariancji, zwany jest powszechnie, od nazwiska autora, testem bartleita.

Bardzo często omawiany test Bartleita jest stosowany dla sprawdzenia założenia o jednakowych wariancjach we wszystkich badanych grupach, przy stosowaniu testu analizy wariancji dla hipotezy o równości wiciu średnich. Test Bartleita oparty jest na pewnej statystyce, która ma rozkład asymptotyczny £². Zbieżność do rozkładu y² jest przy tym bardzo szybka, tak że można stosować rozkład y² nawet dla bardzo małyfch prób.

W literaturze znanych jest kilka postaci wzoru na statystykę y⁷ w teście Banletta. Aby uniknąć kłopotów' 2 logarytmami naturalnymi, na jakie mógłby natknąć się czytelnik nie mający odpowiednich tablic, w niniejszej książce podana będzie postać wzoru 2 wykorzystaniem jedynie logaiytmów

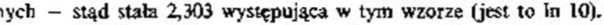
Ze względu na dużą liczbę pracochłonnych rachunków, jakie trzeba wykonać w tym teście, oraz w związku z koniecznością zachowania odpo-

biedniej dokładności obliczeń, zaleca się przy teście Bartletta korzystanie 7 elektrycznych arytmometrów.

Model. Danych jest k populacji normalnych    c_{) (;'=■!. 2.....k).

Z każdej 7 tych populacji wylosowano niezależnie do próby n_i elementów. Mamy więc k losowych prób o liczebnokiach n,. Wyniki każdej próby oznaczamy symbolem .v_;> (/= 1,2.....k,j=* 1, 2.....n,). a ich średnie sym

bolem x_{. Na podstawie tych wyników prób chcemy sprawdzić hipotezę o jednakowych wariancjach we wszystkich populacjach, tj. hipotezę H₀\ c\=o\— ...-cl. wobec hipotezy alternatywnej H_y: nie wszystkie tc wariancje są równe.

Test istotności dla tej hipotezy jesi następujący. 2 wyników k prób o liczebnościach n_; obliczamy według następujących wzorów kolejno P* s², c:

<2.ii.)

/ij—j j= i

n—K /-i    n — k i -1 j-1

12.13)

3(h — I) \    , Mj— ł n-k)

k

gdzie «= Xⁿć- Następnie obliczamy wartość statystyki y- według wzoru r= >

2 303    ^ł

(2.14)    /* = -    - [(_fl-A-)logs²- Y (^-i) jogsf] .

c    t= i

gdzie symbole Jogarytmów oznaczają logarytmy dziesiętne.

Statystyka ta ma przy założeniu prawdziwości sprawdzanej hipotezy //_D rozkład asymptotyczny/¹, zk— 1 stopniami swobody. Z tablicy rozkładu Z², dla ustalonego z góry poziomu istotności i i dla k- l stopni swobody, odczytujemy krytyczną wartość yl w taki sposób, by zachodziło P{x²^ ^zl)=a. Nierówność y*^xl określa obszar krytyczny (prawostronny) dla tego testu. Oznacza to, że ilekroć z porównania obliczonej wartości y² z wartością krytyczną yl otrzymamy nierówność x²^Xi; podejmujemy