img259 2

88 Część II. Podstawy mikroekonomii

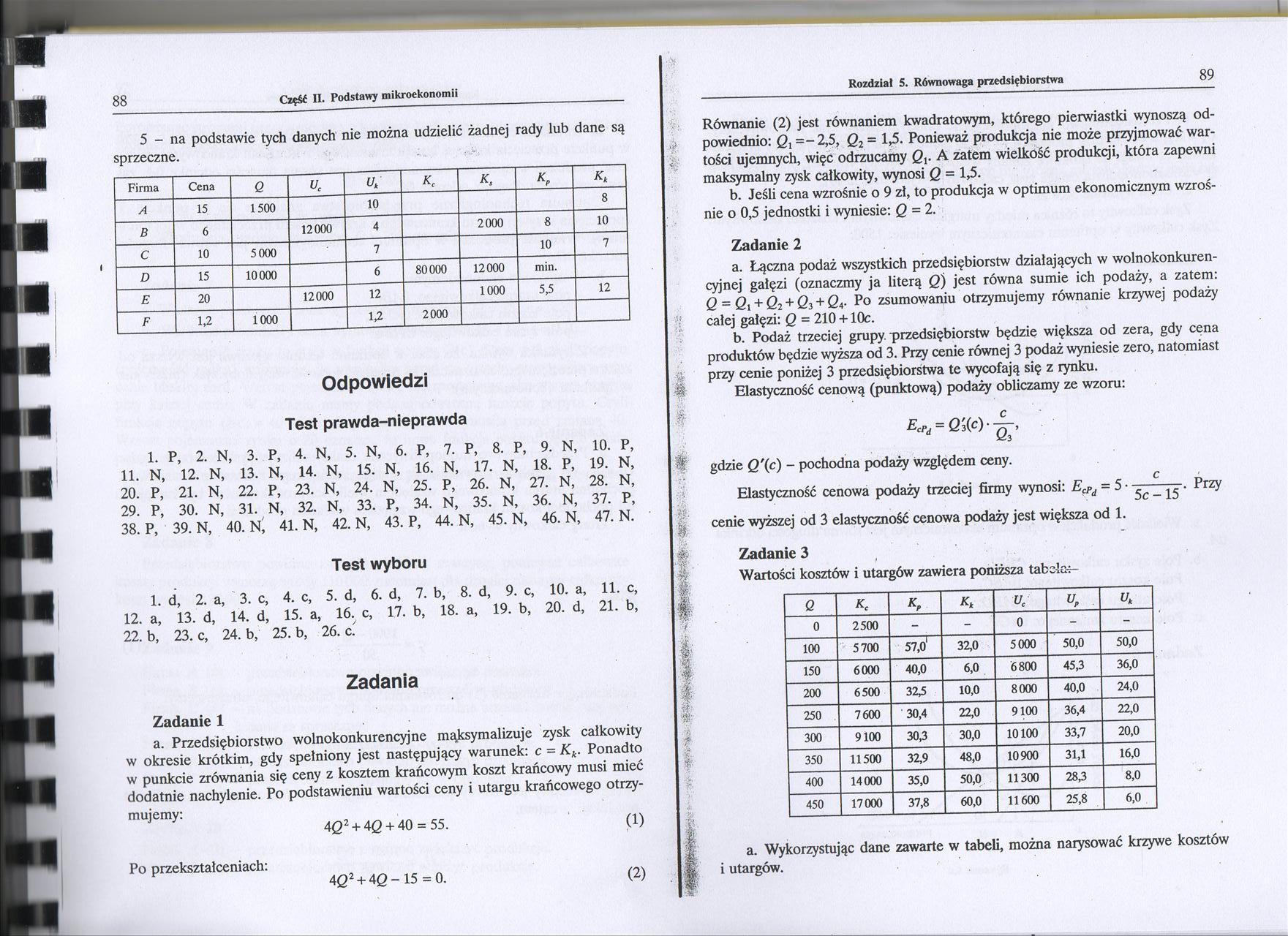
5 - na podstawie tych danych nie można udzielić żadnej rady lub dane są sprzeczne.

Firma	Cena	Q	Uc	Uk	K(	K,		**
A	15	1500		10				8
B	6		12000	4		2000	8	10
C	10	5000		7			10	7
D	15	10000		6	80000	12000	min.
E	20		12000	12		1000	5,5	12
F	1,2	1000		u	2000

Odpowiedzi

Test

prawda-nieprawda

1.

P, 2. N, 3.

P, 4. N, 5. N,

6.

P, 7. P,

8. P,

9.

N,

10.

P,

u.

N,

12. N,

13.

N, 14.

N, 15.

N,

16. N, 17.

N,

18.

P,

19.

N,

20.

P,

21. N,

22.

P, 23.

N, 24.

N,

25. P, 26.

N,

27.

N,

28.

N,

29.

P,

30. N,

31.

N, 32.

N, 33.

P,

34. N, 35.

N,

36.

N,

37.

P,

38.

P,

39. N,

40. n;

41. N,

42. N,

43.

P, 44. N, 45. N,

46

■ N,

47.

N.

Test wyboru

1.

d, 2. a,

3. c,

4. c,

5. d, 6.

d,

7. b, 8. d,

9. c.

, 10. a,

11.

c,

12.

a,

13. d,

14. d,

15. a,

16. c, /

17.

b, 18. a, 19. b,

2C

1. d,

21.

b,

22. b, 23. c, 24. b, 25. b, 26. c.

Zadania

Zadanie 1

a. Przedsiębiorstwo wolnokonkurencyjne mąksymalizuje zysk całkowity w okresie krótkim, gdy spełniony jest następujący warunek: c = K_k. Ponadto w punkcie zrównania się ceny z kosztem krańcowym koszt krańcowy musi mieć dodatnie nachylenie. Po podstawieniu wartości ceny i utargu krańcowego otrzymujemy:

4Q² + 4Q + 40 = 55.    (1)

Po przekształceniach:

Równanie (2) jest równaniem kwadratowym, którego pierwiastki wynoszą odpowiednio: Q_x =-2,5, Q₂ = 1,5. Ponieważ produkcja nie może przyjmować wartości ujemnych, więc odrzucamy Q_v A zatem wielkość produkcji, która zapewni maksymalny zysk całkowity, wynosi Q = 1,5.

b. Jeśli cena wzrośnie o 9 zł, to produkcja w optimum ekonomicznym wzrośnie o 0,5 jednostki i wyniesie: Q = 2.

Zadanie 2

a.    Łączna podaż wszystkich przedsiębiorstw działających w wolnokonkuren-cyjnej gałęzi (oznaczmy ja literą Q) jest równa sumie ich podaży, a zatem: Q = Q\ + 0.2 + Qi + Qą- Po zsumowaniu otrzymujemy równanie krzywej podaży całej gałęzi: Q = 210 + lOc.

b.    Podaż trzeciej grupy, przedsiębiorstw będzie większa od zera, gdy cena produktów będzie wyższa od 3. Przy cenie równej 3 podaż wyniesie zero, natomiast przy cenie poniżej 3 przedsiębiorstwa te wycofają się z rynku.

Elastyczność cenową (punktową) podaży obliczamy ze wzoru:

E_cp_d = Sśfc) * -Q*

gdzie Q\c) - pochodna podaży względem ceny.

c

Elastyczność cenowa podaży trzeciej firmy wynosi: Eęp_d - 5 *    _ —. Przy

cenie wyższej od 3 elastyczność cenowa podaży jest większa od 1.

Zadanie 3

Wartości kosztów i utargów zawiera poniższa tabcfc-

Q			Kk	U'	V,	Uk
0	2500	-	-	0	-	-
100	5700	57,o'	32,0	5000	50,0	50,0
150	6000	40,0	6,0	6800	45,3	36,0
200	6500	32^	10,0	8000	40,0	24,0
250	7600	'30,4	22,0	9100	36,4	22,0
300	9100	30,3	30,0	10100	33,7	20,0
350	11500	32,9	48,0	10900	31,1	16,0
400	14000	35,0	50,0	11300	283	8,0
450	17000	37,8	60,0	11600	25,8	6,0

a. Wykorzystując dane zawarte w tabeli, można narysować krzywe kosztów i utargów.