Kotwica0101

200 6. Projekłoioanie belek drewnianych

200 6. Projekłoioanie belek drewnianych

a)

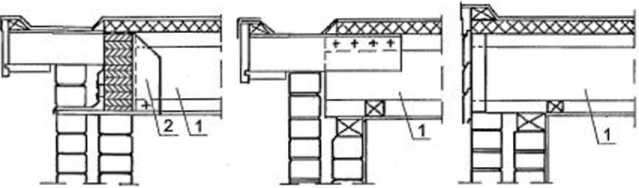
Rysunek 6.34. Oparcie belki dwuteowej ze środnikiem ze sklejki: a) na konstrukcji stalowej, b) na belce klejonej, c) na belce stalowej, d) na murze, e) na ścianie (belce) żelbetowej; 1 - belka, 2 - okucie stalowe

a)

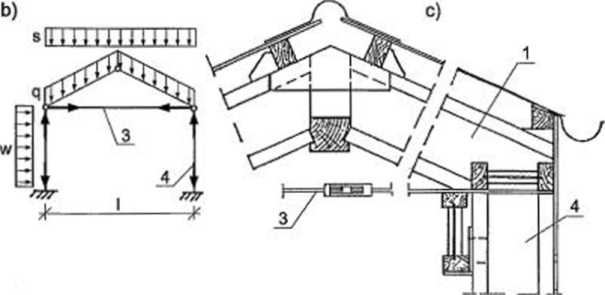
Rysunek 635. Belki stropodachowe ze środnikiem ze sklejki: a) sposoby oparcia belki, b) sdiemat statyczny konstrukcji kozłowej ze ściągiem, c) detale konstrukcyjne węzłów kalenicowego i podporowego; 1 - belka, 2 - okucie stalowe, 3 - ściąg stalowy, 4 - słup

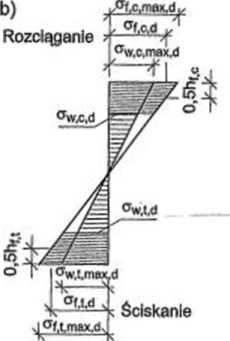
Obliczenia statyczne przeprowadza się przy założeniu liniowej zmienności naprężeń normalnych w przekroju (rys. 6.36) (wg PN-B-03151-.2000).

a)

y	m	4:
		j
u	m

Rysunek 6.36. Belki o przekroju dwu-leowym i skrzynkowym ze środnikiem ze sklejki lub twardej płyty pilśniowej wg PN-B-03151:2000: a) przekroje, b) rozkład naprężeń; b - szerokość pasa, b_w - szerokość środnika, /i/_tC - wysokość pasa ściskanego, hfj - wysokość pasa rozciąganego, h_w - odległość między pasami

W pasie ściskanym powinny być spełnione warunki:

(6.53)

(6.54)

Gf,c,max,d ^ fm/i ®f,cjS ^ kcfc$4

gdzie:

Gf,c,max,d — maksymalne obliczeniowe naprężenie ściskające w pasie, N/mrn², (Jf,_c,d — średnie obliczeniowe naprężenie ściskające w pasie, N/mm², k_c — współczynnik niestaleczności bocznej pasa ściskanego.

Współczynnik k_c należy przyjąć jak w przypadku elementu ściskanego (p. 4.2.2), w zależności od zastępczej smuklości pasa, obliczonej ze wzoru

K = ^n/12    (6.55)

gdzie:

lc — rozstaw stężeń bocznych pasa ściskanego lub odległość między przekrojami zabezpieczonymi przed obrotem, i przemieszczeniami bocznymi, mm, h — szerokość pasa belki, mm.

Naprężenia normalne w pasie rozciąganym powinny spełniać warunki:

Gff_smax4 ^ fm-4    (6.56)

< ffl,d    (6.57)

gdzie:

GfjstuuJ — maksymalne obliczeniowe naprężenia rozciągające w pasie, N/mm², — średnie obliczeniowe naprężenia rozciągające w pasie, N/mm².