mat2 sciaga mini twierdzenia

Twierdzenie 3 (Schwarza).

Jeżeli funkcja f: X-»9?, Xc$Rⁿ ma pochodne mieszane rzędu k i są one ciągłe w punkcie aeX, to te, które różnią się tylko kolejnością różniczkowań, są równe w tym punkcie.

Różniczkę rzędu drugiego określamy jako różniczkę pierwszej różniczki: d^ :=d(df). Ogólnie: d"f :=d(d"~¹f).

Dla funkcji dwóch zmiennych f(x,y) mamy:

d^ = ....= f_Xxdx²+2fxydxdy+fyydy².

d f

•dx^{n k}dy^k , dy^k:=(dy)^k

^dnf k?Ak;9xⁿ-^kay"

Twierdzenie 6 (warunek wystarczający istnienia ekstremum dla funkcji dwóch zmiennych).

Jeżeli w pewnym otoczeniu U punktu (xo,y₀) funkcja f: U ->9t, U<=9?² spełnia warunki: 1°. feC²(U);

2°. fx(x₀.y₀)=f;(x₀.y₀)=o;

3°. det f "(Xo,y₀)=f" (x₀,y₀). f" (X₀,y₀)-(f" (x₀,y₀))² > 0, to funkcja f ma ekstremum w punkcie (Xo,yo), przy czym: f«(x₀.y₀) > ⁰ => f(Xo.yo)= minf(x,y);

^f«(*0.y₀) < 0 => f(x₀,y₀)= maxf(x,y).

Jeżeli det f "(xo,yo) < 0, to funkcja f nie ma ekstremum.

Twierdzenie 2 (o pochodnej funkcji uwikłanej).

' Jeżeli funkcja F jest w otoczeniu punktu (xo,u₀)e9łⁿ⁺¹ funkcją klasy C¹,

’ przy czym F(xo,u₀)=0 i F_u'(x₀,u₀)^0, to funkcja uwikłana u=f(x) określona równaniem , F(x,u)=0 jest w pewnym otoczeniu U punktu x₀ funkcją klasy C¹ i:

Twierdzenie 3 (o zamianie zmiennych w całce potrójnej).

Jeżeli:

1.    funkcja f: V->3t jest ciągła w obszarze regularnym i domkniętym VrfR³,

2.    odwzorowanie bijektywne : n o V określone równaniami: fx = x(u,v,w),

I y = y(x, y, w), jest klasy C¹(fi),

[z = z(x, y, w),

3.    jakobian J(u,v,w) odwzorowania y jest ograniczony i różny od zera wewnątrz obszaru O,

to zachodzi równość:

JJJf(x,y,z)dxdydz= JJJf[x(u,v, wMu.y.w^zfu.y.wJlJfu.y.wJIdudydw.

V    Q

Twierdzenie 3 (o zamianie całki krzywoliniowej nieskierowanej na całkę oznaczoną).

Jeżeli funkcja f jest ciągła na łuku gładkim r={(x(t),y(t)): te[a,p], to Jf(x, y)dl = Jf(x(t),y(t))V[x'(t)f + [y'(t)f dt.

Ta    ^/

Twierdzenie 1 (o zamianie całki powierzchniowej niezorientowanej na całkę podwójną).

Jeżeli funkcja g jest ciągła na płacie gładkim S={(x,y,z): z=f(x,y), (x,y) eD}, gdzie DriR² jest obszarem regularnym, to

JJg(x,y,z)dS = JJg(x,y,f(x,»)^1 + [f;f + [f_yJ dxdy

IV. Równanie liniowe. <r ^    ^

Równanie różniczkowe, które można zapisać w postaci:    „,    „    a

y'+p(x)y=g(x) “f ‘ TTT

nazywamy równaniem liniowym pierwszego rzędu.

Jeśli g(x)=0, to równanie nazywamy równaniem liniowym jednorodnym(albo uproszczonym). Będzie to wtedy równanie o zmiennych rozdzielonych.

1. Rozwiązujemy najpierw równanie jednorodne.

•Utwto J-    /

VxeU:

f'(x) = -

F'(x,u)

F'(x,u)

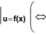
df_

axj

^F*i

Ti

1,2.....n

nanie lednoroane.    ^ In

1

= -p(x)dx => ln|y| = - Jp(x)dx+ln|c| => y = ce ^,p(x)dx

V

-o

-RORJ

Twierdzenie 5 (o zamianie całki podwójnej na całki iterowane).

2. Rozwiązanie ogólne równania niejednorodnego wyznaczymy stosując M.U.: (metodę uzmienniania stałej).

Jeżeli funkcja f: D-»SR jest ciągła w obszarze D c9t² normalnym względem osi OX:

D= {(x,y)e9*²: a < x < b a cp(x) < y < \j/(x)}, to

jjf(x.y)dxdy = Jj Jf(x,y)dy

_<P(x)

b i|>(x)

dx = Jdx Jf(x,y)dy

W

Twierdzenie 1 (o zamianie zmiennych w całce podwójnej), ć I

Jeżeli:

1. funkcja f: D->tR jest ciągła w obszarze regularnym i domkniętym D c9r,

2. odwzorowanie bijektywne v(/: A<-»D określone równaniami:

Jx = x(u,v), ly = y(u,v),

jest klasy C¹(A),

3. jakobian J(u,v) odwzorowania vj/ jest ograniczony i różny od zera wewnątrz obszaru A, to zachodzi równość:

Twierdzenie 4 (o rozwiązaniu ogólnym równania liniowego jednorodnego n-tego rzędu).

Jeżeli funkcje y,, y₂,... ,y_n tworzą fundamentalny układ rozwiązań równania (2) w przedziale (a,b), to kombinacja liniowa tych funkcji: y(x) = X^kVk(^x)

z dowolnymi stałymi Ci, C₂.....C„ jest rozwiązaniem ogólnym

tego równania w rozważanym przedziale.

Twierdzenie 1 (o istnieniu funkcji uwikłanej).

Jeżeli funkcja F jest ciągła w otoczeniu punktu (xo,Uo)e9tⁿ⁺¹ , i ma w tym otoczeniu ciągłą pochodną F_u', przy czym F(x₀,u₀)=0 i F_u'(xo,u₀)*0, , to istnieje takie otoczenie U₀ punktu (xo,u₀), w którym równanie F(x,u)=0 . posiada tylko jedno rozwiązanie u=f(x) będące funkcją ciągłą . w pewnym otoczeniu punktu x₀, przy czym f(x₀)=u₀.

JJf (x, y )dxdy = JJf [x(u, v), y(u, v)] • | J(u, v)|dudv.

D    A

Twierdzenie 2 (o zamianie całki potrójnej na całki iterowane).

Jeżeli funkcja f: V-»9? jest ciągła w obszarze V c5R³ normalnym względem płaszczyzny XOY: V= {(x,y,z)e$R³: (x,y) eD a cp(x,y) ^ z < v(x,y)}, to

jjjf(x,y,z)dxdydz = JJ

V    D

ip(x.y)

Jf(x,y,z)dz

_«p(x,y)

>c(x.y)

dxdy=JJdxdy Jf(x,y,z)dz.

D    <f>(x,y)