20121023078

Twierdzenie Greena
jeżeli funkcje P i Q są klasy C’ wewnątrz obszaru normalnego O krzywa K iesl brzeg em obszaru O t jest zorientowana dodatnio to
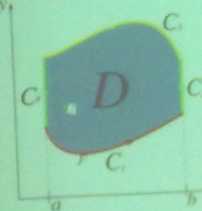
f(PdX + Qdy) = J] (f-f )*''!'
K D
dP
Jeśli
du
Pd»+Cłdy=dF
to możemy iwftwto o riwcg* *.upetr» t pole F=(P,Q) j**1 polem polenc|alnym
Przykład praca po drodze zatnkn*sM IV . Jrod,i - jPdi + Qd9.
Wyszukiwarka
Podobne podstrony:
Twierdzenie Greena Jeżeli funkcje P i Q są klasy C1 wewnątrz obszaru normalnego O, krzywa K jest brz
8(1) Twierdzenie Grccna Jeżeli funkcje P(x, y) i Q{xt y) są klasy Cl w obszarze normalnym D (względe
Rozdział 1. Teoria popytu Twierdzenie 1.7. Jeżeli funkcja u jest klasy C2 i macierz &nbs
mat2 sciaga mini twierdzenia Twierdzenie 3 (Schwarza). Jeżeli funkcja f: X-»9?, Xc$Rn ma pochodne mi
TWIERDZENIE. Jeżeli funkcje _/(*) i g(x) są różniczkowalne na zbiorze X, to dla każdego xeX (cf (a:)
6(1) Twierdzenie o zamianie całki krzywolinoliniowej skierowanej w Rż Jeżeli funkcje P(x, y) i Q(x,y
© Twierdzenie (O zamianę całki krzywoliniowej skierowanej na całkę pojedyncza) Jeżeli funkcje P i Q
Lagrange a Twierdzenie Lagrange’a Jeżeli funkcja/jest ciągła w przedziale [a, b] oraz różniczkowalna
Granica i ciaglosc fukcji stre 85. Udowodnić następujące twierdzenie, zwane twierdzeniem Stolza Jeże
• Fakt 1.2.3 (całka lónnuutiu o zmiennych tnzAnclont/chJ Jeżeli funkcjr p(t) i A({
Twierdzenie 6.8 (Taylora) Jeżeli funkcja f ma ciągle pochodne cząstkowe do drugiego rzędu włącznie n
Fakt 6.1.8 (interpretacja geometryczna twierdzenia Fermata) Jeżeli funkcja ma ekstremum lokalne w pu
Rolle a Twierdzenie Rolle’a Jeżeli funkcja/jest ciągła w przedziale [a, b] oraz różniczkowalna w prz
więcej podobnych podstron