Rzuty mongea134

77

8.4. Inne powierzchnie nieobrotowe

Wspomniane wcześniej powierzchnie - walcowa i stożkowa mogą występować także w wersji nieobrotowej. Ponieważ w tej wersji zachowują swoją prostokreślność i rozwijalność, w technice bywają wykorzystywane równie chętnie jak ich obrotowe odpowiedniki.

Obydwie powierzchnie nieobrotowe tworzy się podobnie (szkice na rys.74a i b): na dowolnej płaszczyźnie a obiera się krzywą c², czyli tzw. krzywą kierującą. Przez kolejne punkty krzywej prowadzi się proste - tworzące powierzchni.

Powierzchnię stożkową nieobrotową (rys. 74 a) tworzy zbiór tworzących, które przechodzą przez punkty kierującej c² oraz przez nienależący do a punkt właściwy W - wierzchołek stożka. Ponieważ tworzące są prostymi, a nie tylko ich odcinkami, więc powierzchnia stożkowa znajduje się po obydwóch stronach wierzchołka W i poniżej a, co zaznaczono na szkicu 74a.

Powierzchnię walcową nieobrotową (rys.74 b) tworzy zbiór prostych tworzących t, przecinających kierującą c² i równoległych do dowolnego kierunku k, który nie może być równoległy do a.

Krzywa kierująca, narysowana na szkicach a i b i opisana jako c², faktycznie nie jest żadną z krzywych c², bowiem dla bardziej wyrazistego rysunku została tu narysowana tylko symbolicznie.

a)

b)

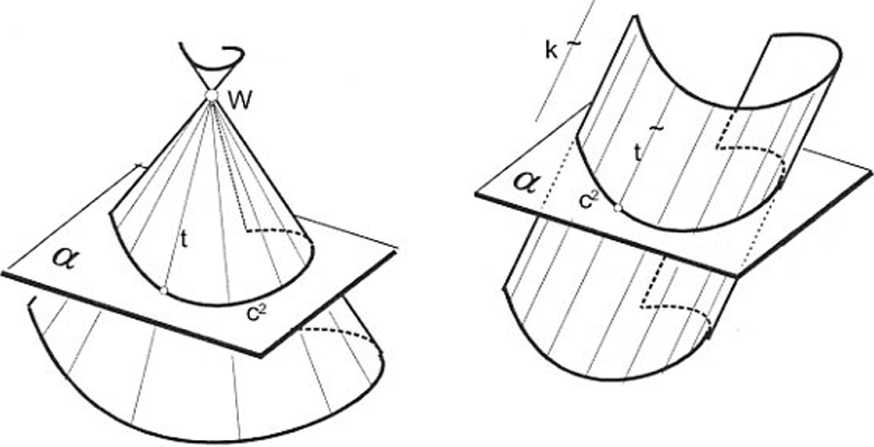
Rys. 74