Rzuty mongea128

70

8.1. Powierzchnie prostokreślne obrotowe

Najprostszym przykładem powierzchni obrotowej, prostokreślnej i roz wijalnej jest powierzchnia walcowa obrotowa.

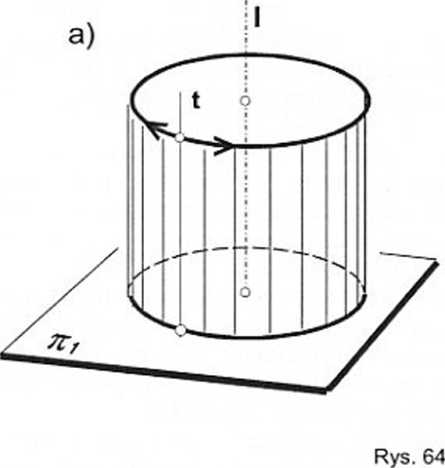
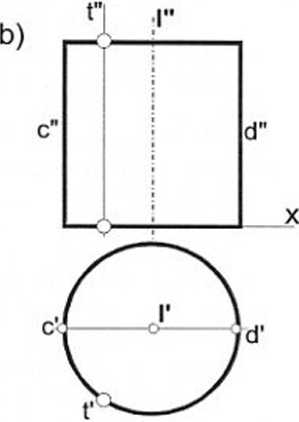
Jest ona tworzona przez kolejne położenia prostej t (rys. 64 a, b) obracanej wokół równoległej do niej prostej I, zwanej osią obrotu. Obracająca się prosta t nazywa się tworzącą powierzchni, bowiem zbiór kolejnych położeń prostej t tworzy tę powierzchnię. Rys. 64a szkicowo pokazuje „przestrzennie" fragment takiej powierzchni, który odwzorowano na rys. 64b. Ponieważ oś I i tworzące t są prostopadłe do rzutni 7n, więc rzutem powierzchni na tti jest okrąg, którego średnica jest równa średnicy powierzchni (powierzchnia jest poziomorzutująca).

Rzut pionowy to tylko dwie tworzące konturowe c" i d" oraz rzuty okręgów ograniczających ten fragment powierzchni.

Teoretycznie długości tworzących t powierzchni są nieograniczone, ale w zastosowaniach korzysta się z ich skończonych długości. Zagadnienie roz-wijalności powierzchni walcowej zostanie omówione w podrozdziale 9.3.

Innym przykładem powierzchni obrotowej, prostokreślnej i rozwijalnej

jest powierzchnia stożkowa obrotowa. Tworzona jest także przez kolejne położenia tworzącej t obracanej wokół osi I. Jednak w tym przypadku tworząca t przecina oś I w punkcie W - wierzchołku stożka. Ponieważ tworzące t stożka są prostymi (a nie odcinkami o ograniczonej długości), więc powierzchnia stożkowa teoretycznie istnieje po obu stronach wierzchołka W.

Szkic na rys. 65a ilustruje „przestrzennie” fragmenty powierzchni stożkowej o osi I prostopadłej do m, natomiast na rys. 65b odwzorowano tylko ten jej fragment, który od góry jest ograniczony wierzchołkiem W, a z dołu rzutnią. xn.

Rozwinięcie tej powierzchni omówiono w podrozdziale 10.3 (rys. 84).