wyklad2c

Gradientem funkcji (f) w punkcie x nazywamy (o ile istnieje) wektor, który wskazuje kierunek i zwrot najszybszego, przy max. wzrostu (przy min. spadku) wartości funkcji celu w danym punkcie dziedziny

dx_ł    dx₂

= [^ci>^czT

Izokwanta jest prosta prostopadła do aradientu
	funkcji.
,x,) G 9? seD?^v	: clxl + c2x2 = z)- prosta _L V
x2
	\^Z1 \^Z2
^C2
	\ i i ^z?^>Zi
	Cl x1

Przykład 1.

Pewne przedsiębiorstwo produkuje dwa wyroby A i B. Do ich wytworzenia używa trzech surowców S_t, S₂, S₃. Zużycie poszczególnych surowców na jednostkę wyrobu, posiadane przez przedsiębiorstwo zasoby oraz zysk jednostkowy dla wyrobów A i B przedstawia poniższa tablica.

Surowce	Zużycie surowca na jednostkę produkcji		Zasoby surowców
	A	B
s,	2	1	8
s,	l	1	5
S3	1	2	10
Zysk	2	1

Ustalić optymalne rozmiary produkcji wyrobów A i B, tak aby zysk uzyskany z ich sprzedaży był jak największy.

Budujemy PL:

x_t- ilość wyrobu A [jedrt.]

x₂- ilość wyrobu B [jedn.]

2xj + x₂ —» max

p.o

2x_x + x₂ < 8 Xj + x₂ < 5 Xj + 2x₂ < 10 Xj, x₂ >0

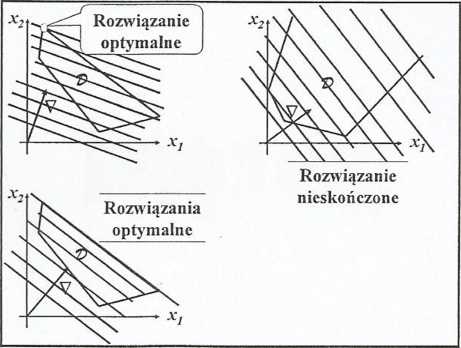
Ponieważ jest to zadanie z dwiema niewiadomymi, więc można je rozwiązać metodą graficzną.

Znajdujemy punkty należące do prostych
2x1 +x2 =8	(0,8); (4,0)
x,+x2 ^= 5	(0,5); (5,0)
Xj + 2x2 =10		(0,5); (10,0)
oraz gradient funkcji	[21
v/ =	1