0210

211

§ 4. Pochodne i różniczki wyższych rzędów

napisane niżej jako obliczone względem zmiennej t otrzymujemy kolejno

dy dxd²y — d²xdy

, dy _n (dy\ dx    dx²

^* dx ’    \dx/_x dx    dx

tj.

(5)

następnie

i ostatecznie (6)

_n dxd²y — d²xdy

/ dxd²y — d²xdy\ (dxd²y-d²xdy\ _ V dx³ ) ^yx* \ ^dxi )x    dx

dx³(dxd³y — d³xdy) — 3 dx²d²x (dxd²y — d²xdy) _    “    dx*

dx

dx (dxd³y — d³xdy) — 3 d²x (dxd²y — d²xdy) itd. Wzory (5), (6),... są najogólniejsze. Jeśli x rozpatrywać w nich jako zmienną niezależną, to d²x,d³x,... staną się zerami i wrócimy do wzorów (4).

Otrzymane przez nas wzory na pochodne funkcji y względem zmiennej x realizują tak zwane różniczkowanie w postaci parametrycznej. Jeśli x i y są dane jako funkcje parametru ł:

x=ę(t), y = v(t),

to jak widzieliśmy w 106, gdy spełnione są odpowiednie warunki, y jest określone jako funkcja y=f{x) zmiennej x. Jeśli istnieją kolejne pochodne zmiennej x i zmiennej y względem t, to istnieją również pochodne zmiennej y względem zmiennej x i wyrażają się przez tamte w postaci wyprowadzonych wyżej wzorów.

Czasami bywa wygodniej wyrażać pochodne y względem x przez pochodne (a nie różniczki) zmiennych x i y względem t. Wyrażenia te łatwo jest otrzymać z wyrażeń przez różniczki dzieląc odpowiednio licznik i mianownik przez dt, dt³, dł⁵,... W ten sposób otrzymujemy wzory

,    dt    y'_t

Vx    i    i ’

dx    x,

~dt

dx d²y d²x dy

dt dt²    dt² dt x'_ty'_t2—x',2y'„

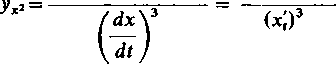
14*